참고 : BaaaaaaaarkingDog | [실전 알고리즘] 0x14강 - 다익스트라 알고리즘_구버전

다익스트라 알고리즘 구현하다 스스로 얼마나 부족한지 깨달아서 새로 공부한다.
백준 최단경로(1753) 문제를 다시 풀어보며 제대로 내것으로 만들어보자 !

다익스트라, dijkstra

방향 혹은 무방향 그래프에서 하나의 시작점으로부터 다른 모든 정점 까지의 최단 거리를 구하는 알고리즘

• 시작점이 주어지는게 국룰
• 네비게이션 등 최단거리를 찾을 때 사용
  • A* 휴리스틱을 더해 시간복잡도를 효율적으로 만드는 알고리즘도 있지만, 코테에는 휴리스틱이 안나오기 떄문에 다익스트라만 익히면 됨

과정

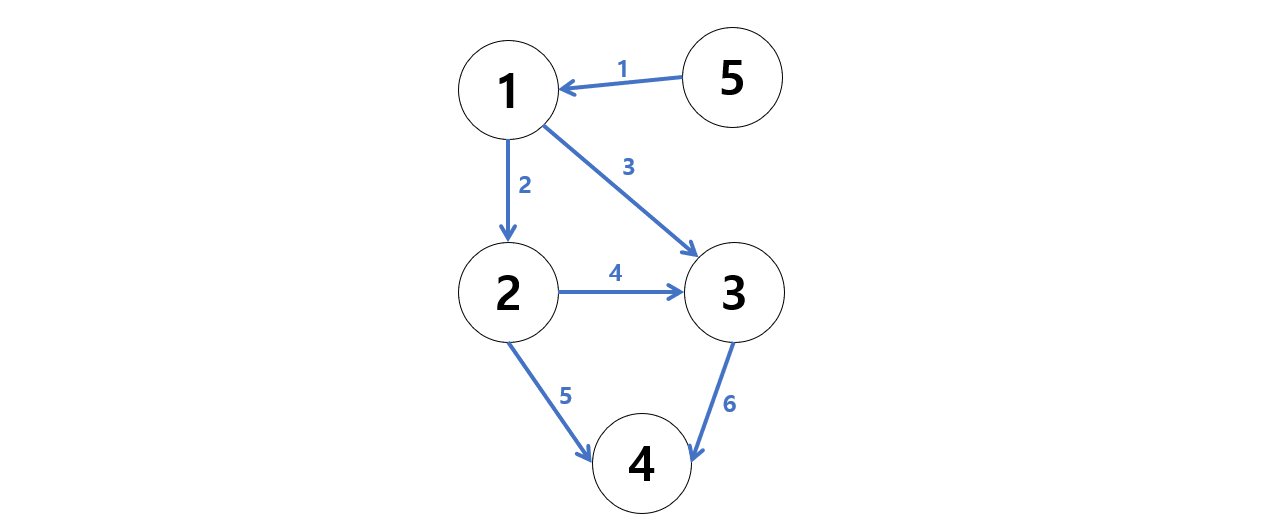
최단경로(1735) 문제를 예시로 살펴보자.

그래프를 그려보면 다음과 같다.

시작정점인 1의 최단거리 테이블을 만들면 다음과 같다.

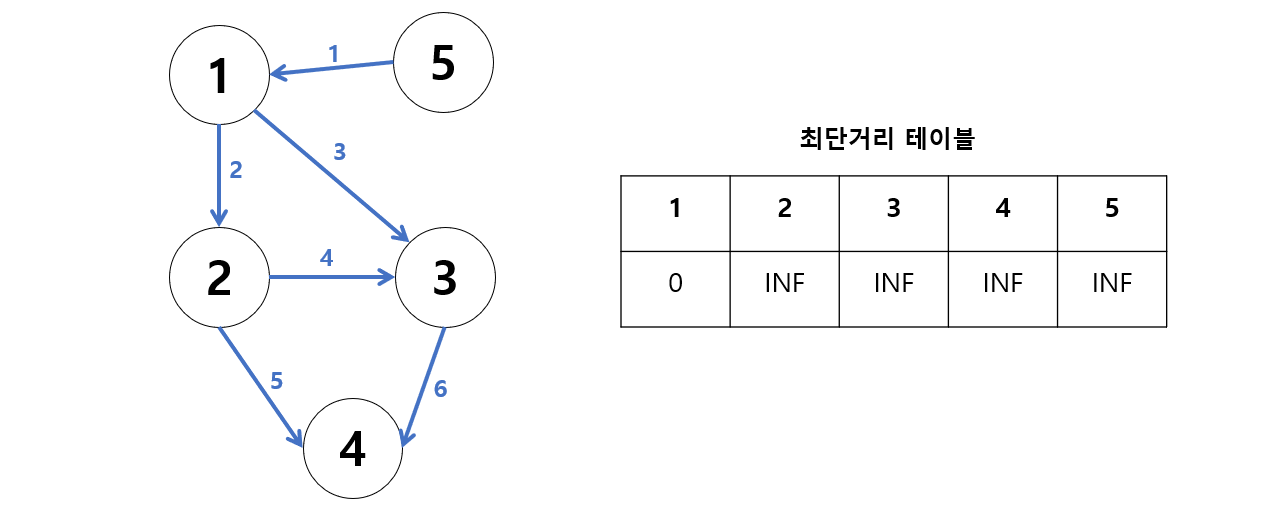
자기 자신으로 가는 비용은 0,
다른 정점으로 가는 비용은 아직 계산 전이므로 무한대로 두어진 상태

1. 최소 비용 찾기

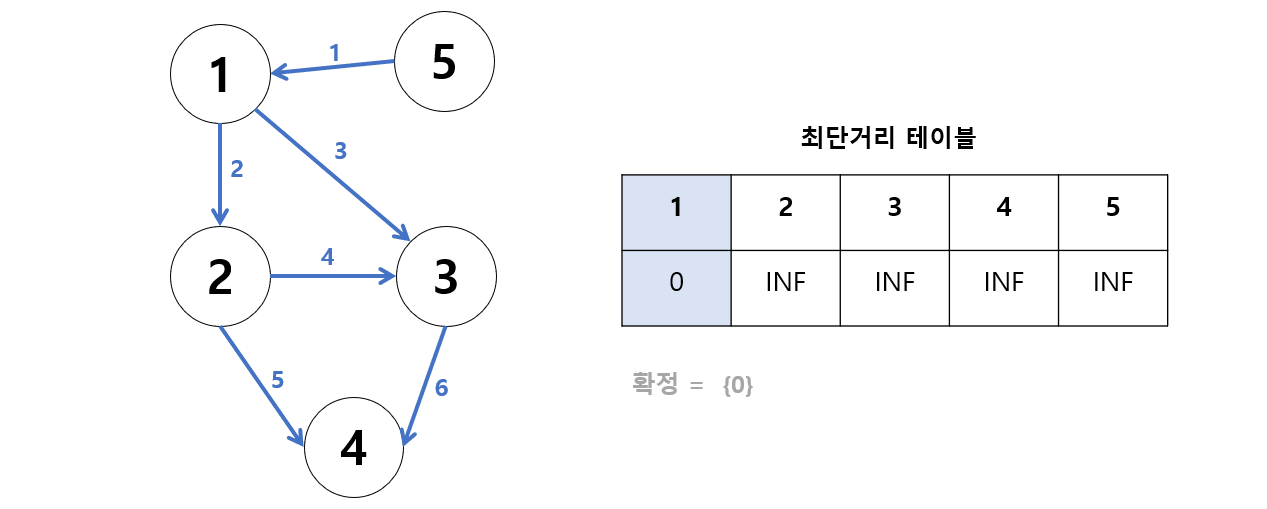
• 테이블에서 현재 가장 작은 값은 0이니까 0을 확정시킨다.
• 1번 정점에서 갈 수 있는 정점은?
  • 2번
  • 3번
• 1번에서 2, 3번 정점으로 갈 때의 최단거리는?
  • 0 + 2 = 2 VS INF
  • 0 + 3 = 3 VS INF

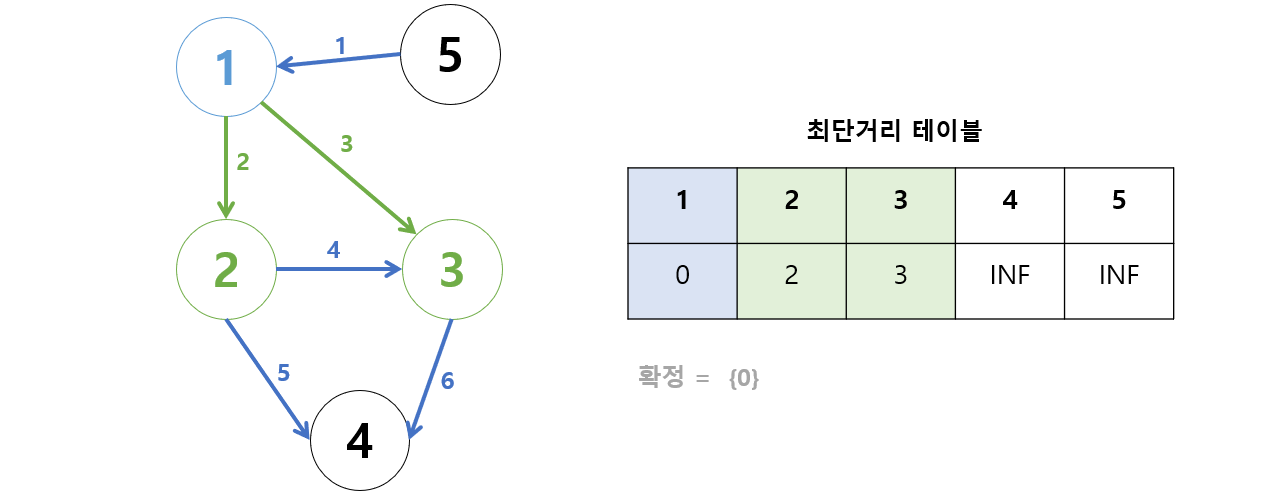
※ 파란색은 확정된 것, 초록색은 (정점계산 후 최단거리가) 변경된 것

테이블이 이렇게 바뀐다.

• 테이블에서 현재 가장 작은 값은? 2이므로 2를 확정시킨다.
• 2번 정점에서 갈 수 있는 정점은?
  • 3번
  • 4번
• 1번에서 3, 4번 정점으로 갈 때의 최단 거리는?
  • 2번을 거친 후 VS 거치지 않은 경우
    • 2 + 4 = 6 VS 3
    • 2 + 5 = 7 VS INF

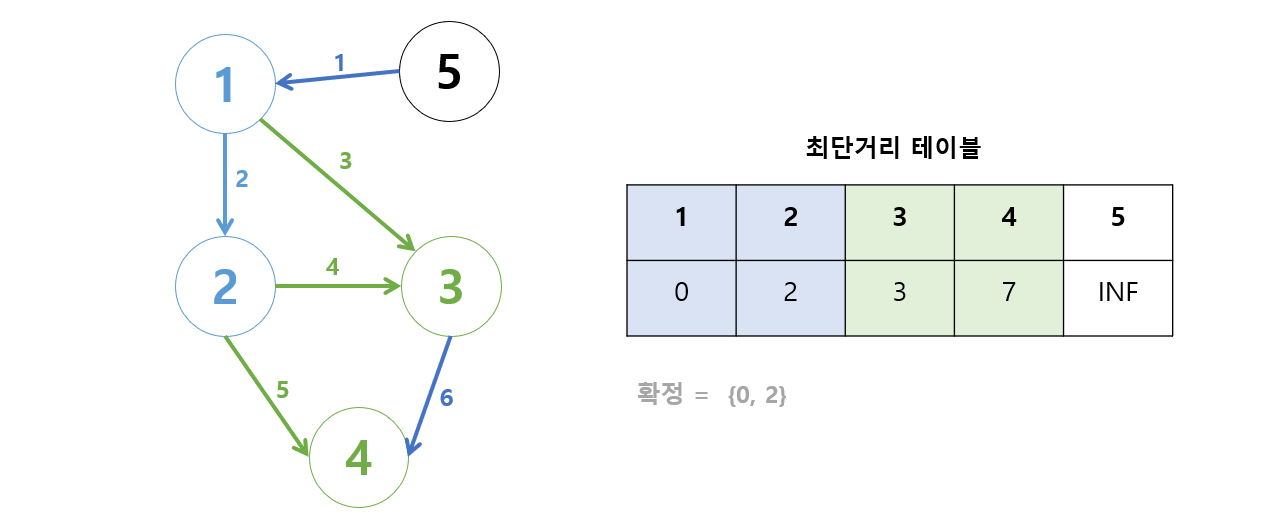
• 테이블에서 현재 가장 작은 값은? 3이므로 3을 확정시킨다.
• 3번 정점에서 갈 수 있는 정점은?
  • 4번
• 1번에서 4번 정점으로 갈 때의 최단거리는?
  • 3번을 거친 후 VS 거치치 않은 경우
    • 3 + 6 = 9 VS 7

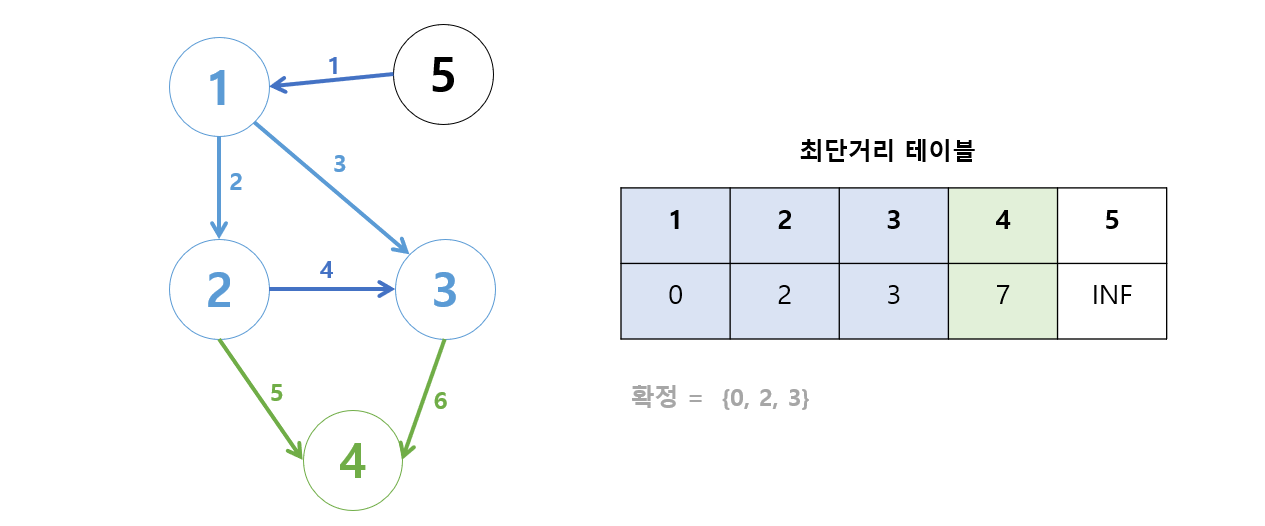
• 테이블에서 현재 가장 작은 값은? 7이므로 7을 확정시킨다.
• 4번 정점에서 갈 수 있는 정점은?
  • 없다

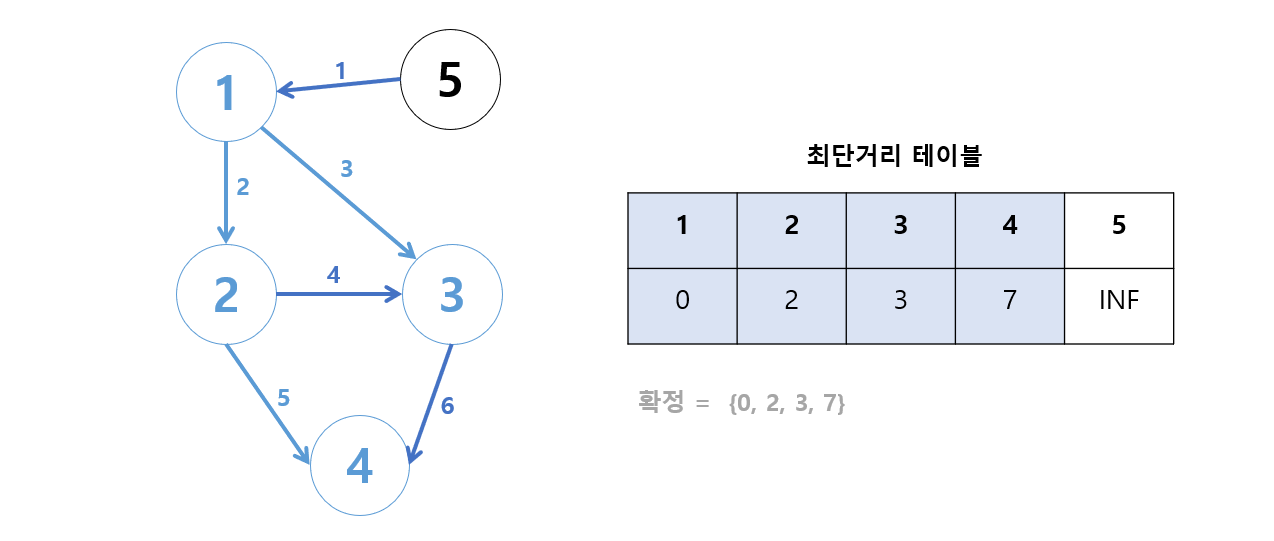
• 테이블에 현재 남아있는 값은? INF이다.
• 5는 어떤 정점에서도 갈 수 없으므로 값이 바뀌지 않았다.
  이에 따라 INF를 확정시킨다.

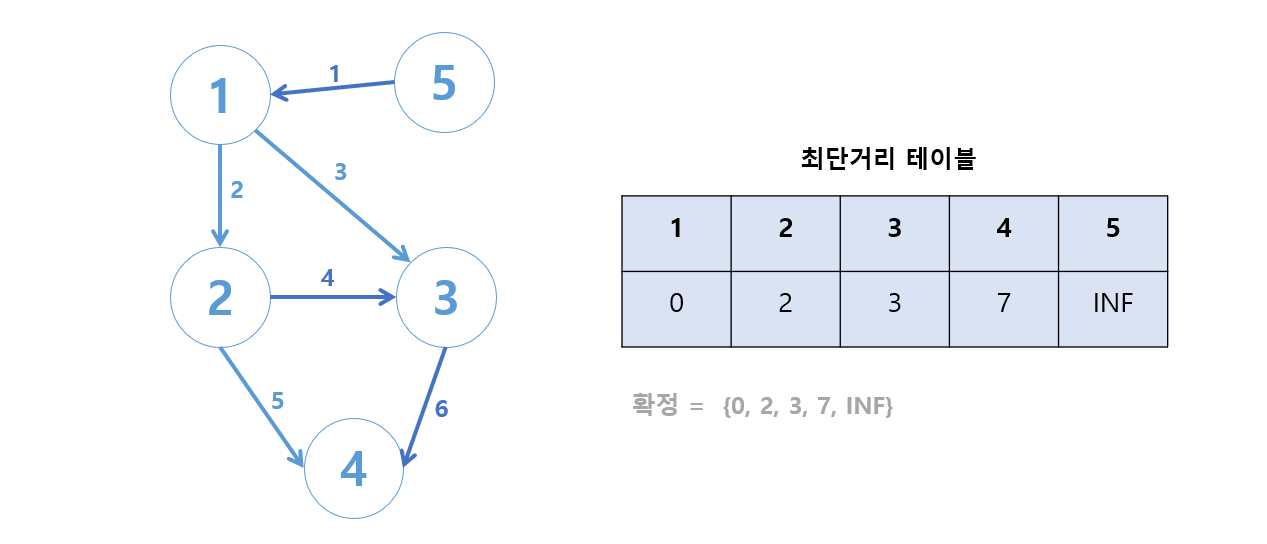
따라서 답은

0
2
3
7
INF

가 나오게 된다.

주의사항

그러나 이를 곧이곧대로 구현하면, 데이터가 많을경우 엄청난 시간초과와 메모리초과에 걸릴 수 있다.

• 각 단계는 V번에 걸쳐 진행된다.
  또한 각 단계마다 현재 남은 모든 정점에 대해 최단거리 테이블을 확인하여 최솟값을 뽑아야 하므로 O(V²)시간이 걸린다.
• 최단거리 테이블 갱신을 위한 연산도 발생한다.
  • 그래프가 인접리스트라면 O[E]
  • 그래프가 인접행렬이라면 O[V²]

구현한 방법에 따라 O(V² + V²) 혹은 O(V² + E) 가 발생한다.

2. 효율적으로 최소 비용 찾기

힙을 사용한다.

사실 아직도 헷갈리는 부분이 좀 많아서 차근차근 정리해보고자 한다.

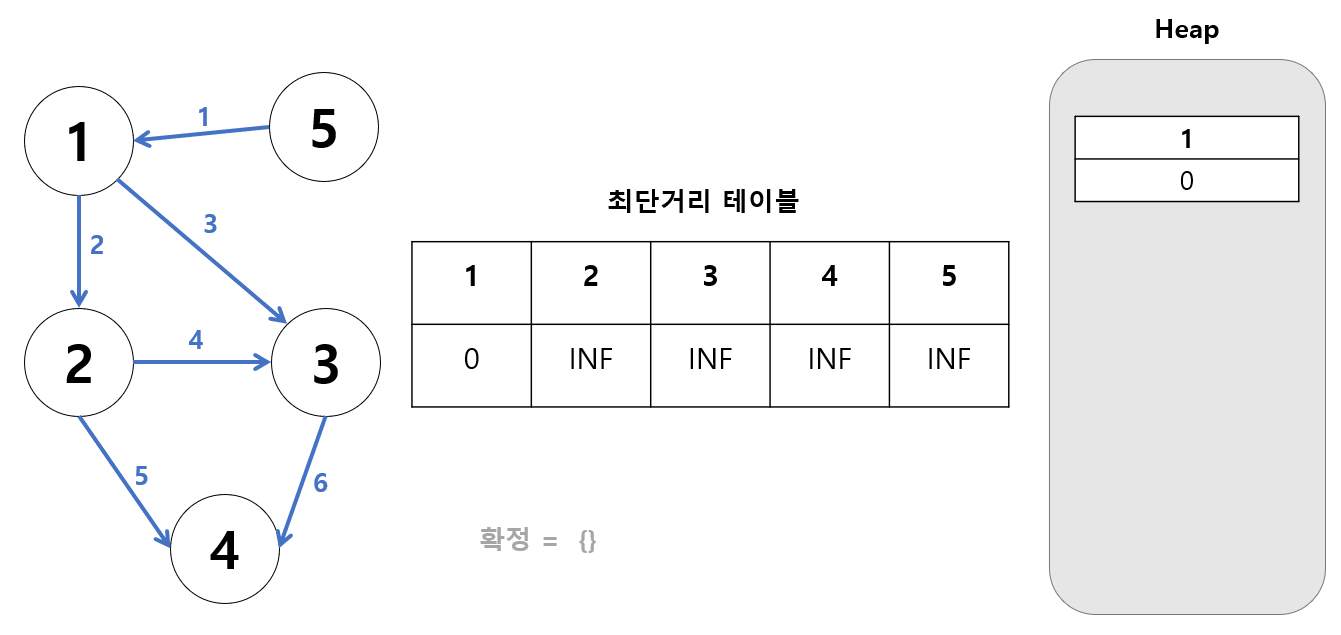
맨 처음에 [시작점, 0]을 힙에 넣어주고 시작한다.
(참고) 나는 {} 형태로 묶어 넣었다.

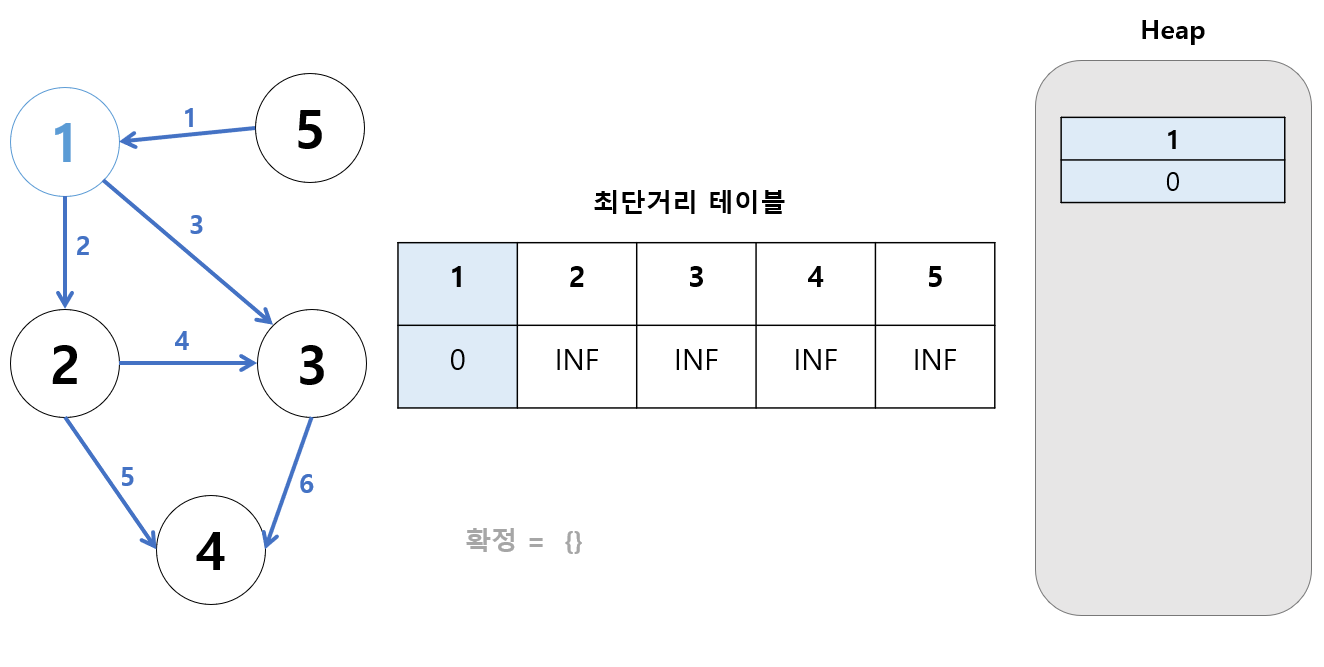
초기 세팅이 끝나면, 본 과정을 시작한다.

• 힙에서 거리가 가장 작은 값은?
  지금 힙에서는 [1, 0] 이 선택된다.
• 최단거리 테이블[1] = 0이 맞는가?
  • 일치하지 않으면 해당 원소 제거하고 넘어간다.
  • 일치하면 과정을 이어간다.

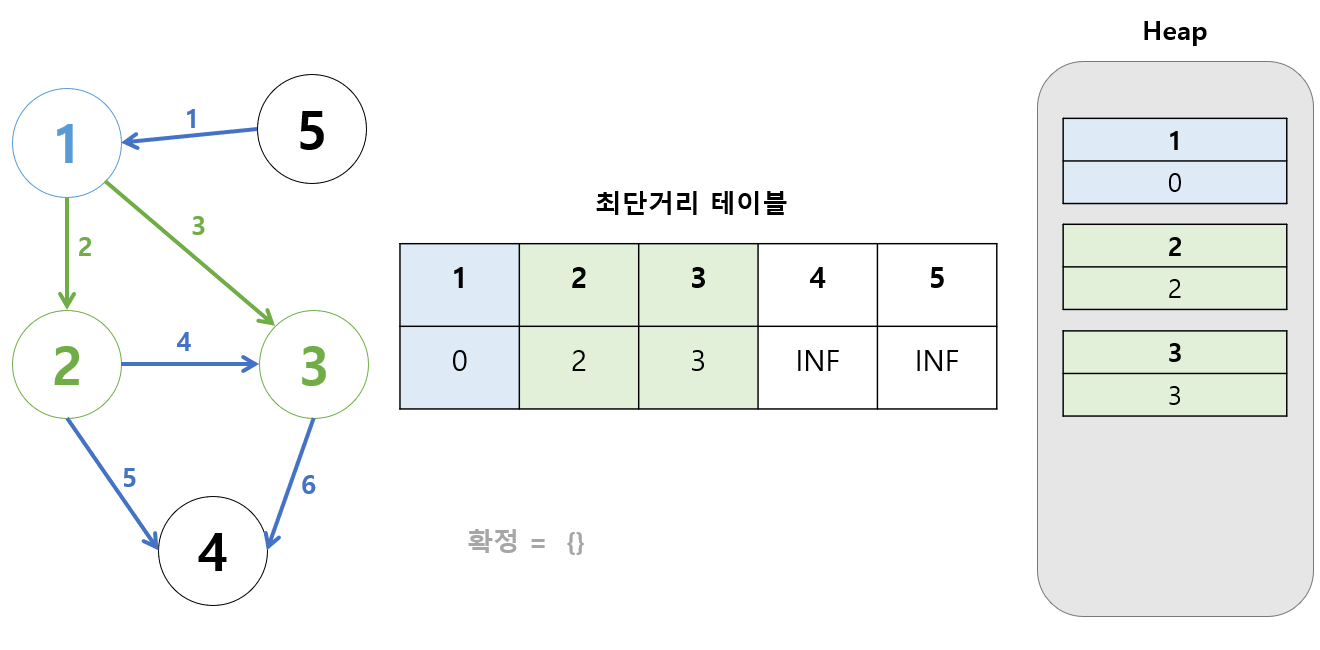
최단거리 테이블[1] = 0이 맞으므로, 1번 정점을 거쳐서 갈 수 있는 정점들의 비용을 계산한다.

• 2번: 0 + 2
• 3번: 0 + 3

이 값이 최단거리 테이블에 저장된 값보다 작으면?

• 최단거리 테이블 값 갱신
• 힙에 삽입

현재 테이블에 저장된 INF 보다 작으므로, 값을 갱신하고 힙에 넣는다.

처리해주었으므로 [1, 0]을 힙에서 제거한다.

• 힙에서 거리가 가장 작은 값은?
  [2, 2]가 가장 작다.
• 최단거리 테이블[2] = 2가 맞는가?
  맞으므로 과정을 이어나간다.

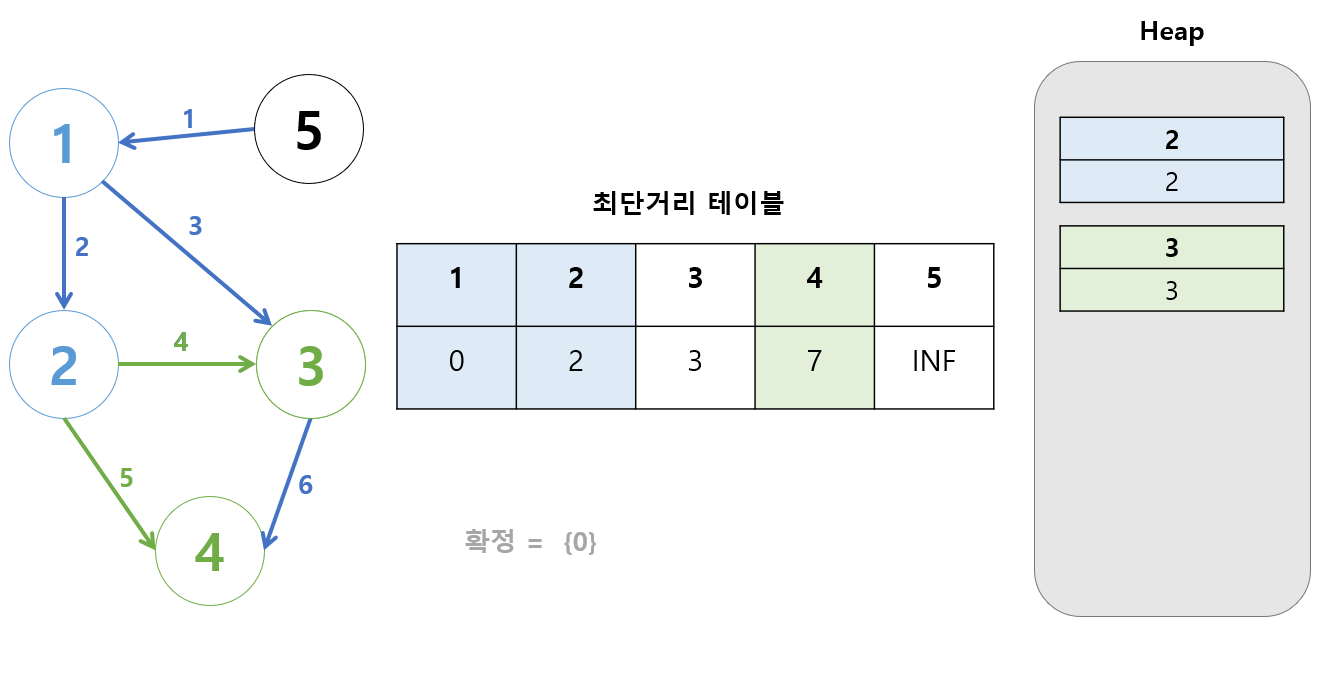
2번 정점을 거쳐서 갈 수 있는 정점을 게산한다.

• 3번: 2 + 4
• 4번: 2 + 5

이 값이 최단거리 테이블에 저장된 값보다 작으면?

• 최단거리 테이블 값 갱신
• 힙에 삽입

4번은 작지만, 3번은 오히려 더 크다!
👉🏻 3번의 경우 위 과정을 깔끔하게 무시한다.

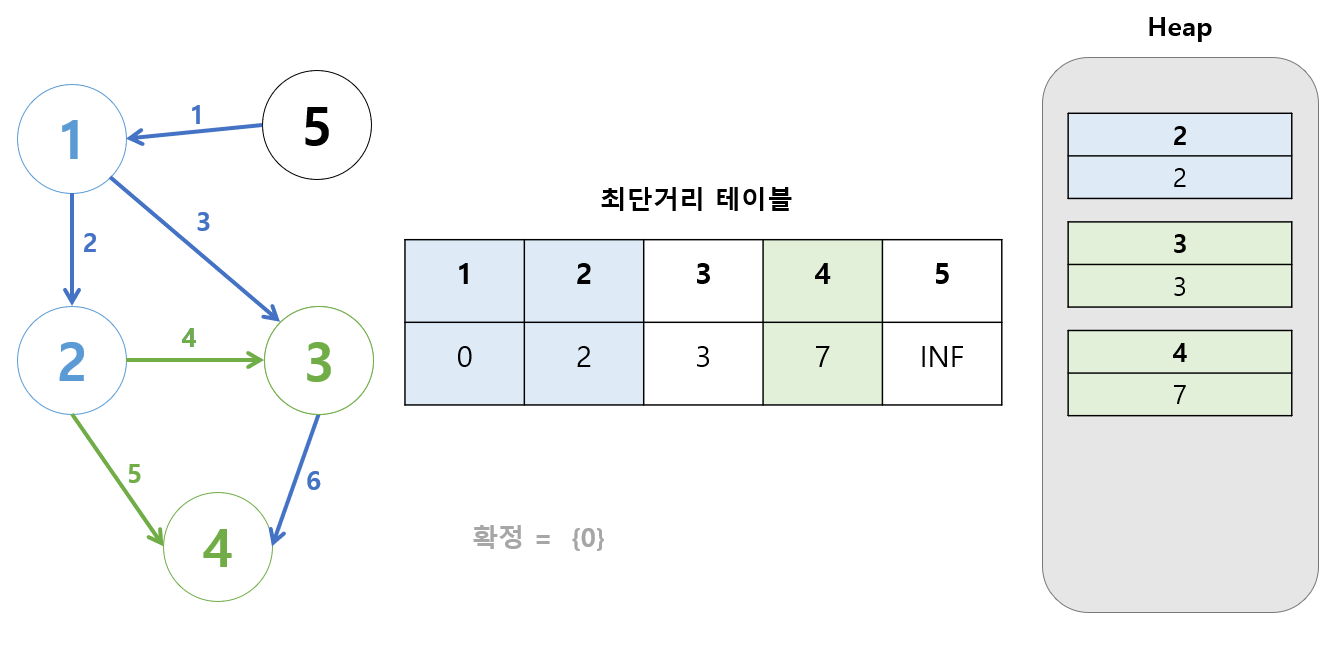
처리가 끝났으므로 [2, 2]를 힙에서 제거한다.

• 힙에서 거리가 가장 작은 값은?
  [3, 3]이 제일 작다.
• 최단거리 테이블[3] = 3 이 맞나?
  맞으므로 과정을 이어나간다.

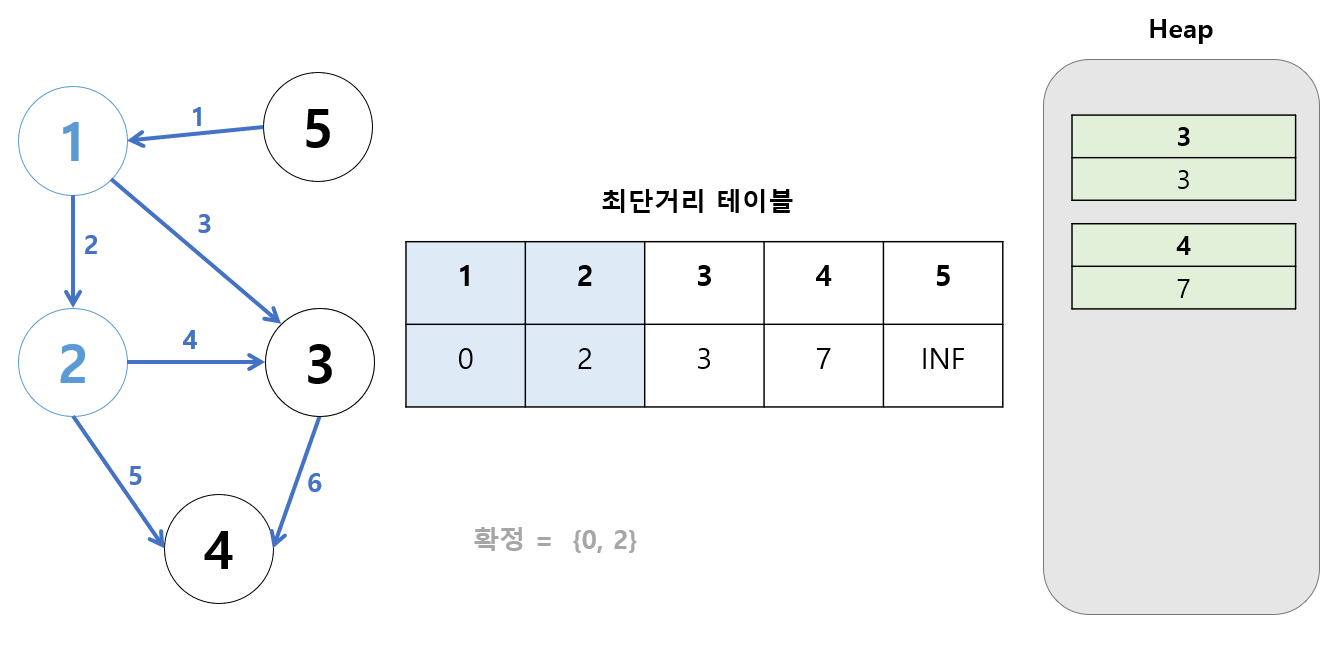
3번 정점을 거쳐 갈 수 있는 정점을 계산한다.

• 4번: 3 + 6

• 이 값이 최단거리 테이블에 저장된 값보다 작은가?
  놉, 더 크다.

따라서 무시한다.
처리가 끝났으므로 [3, 3] 을 제거한다.

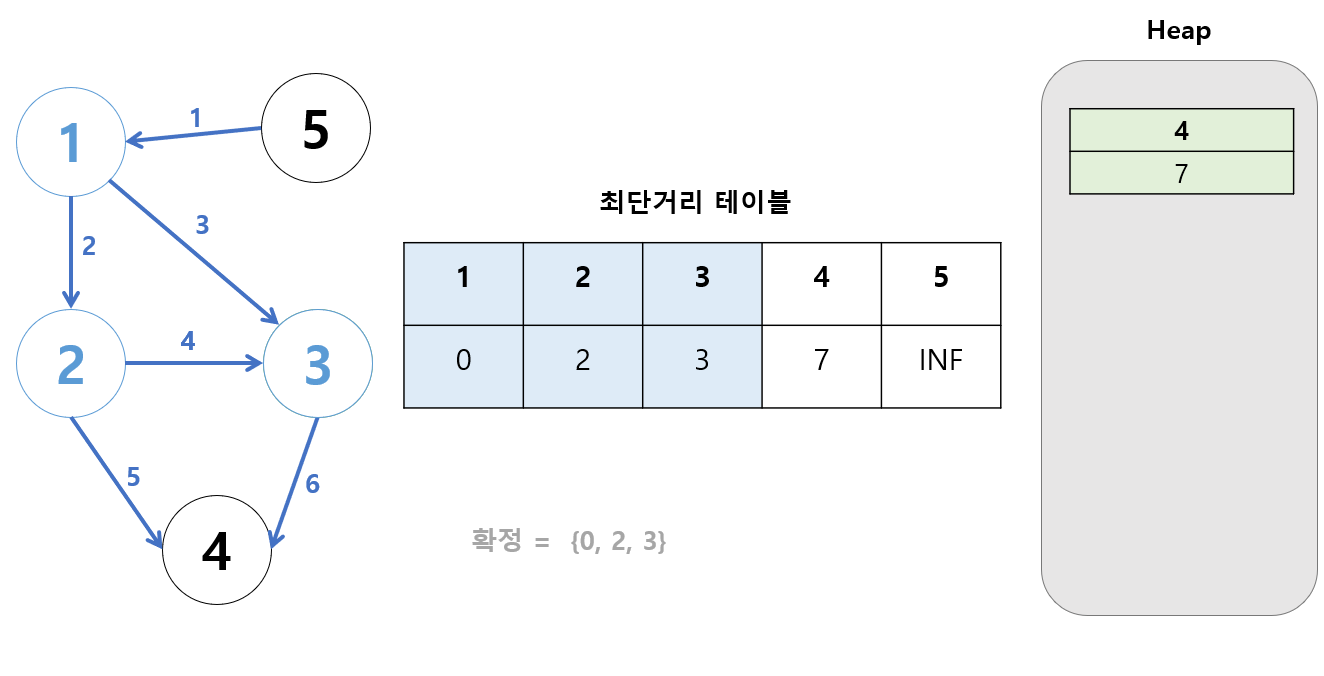
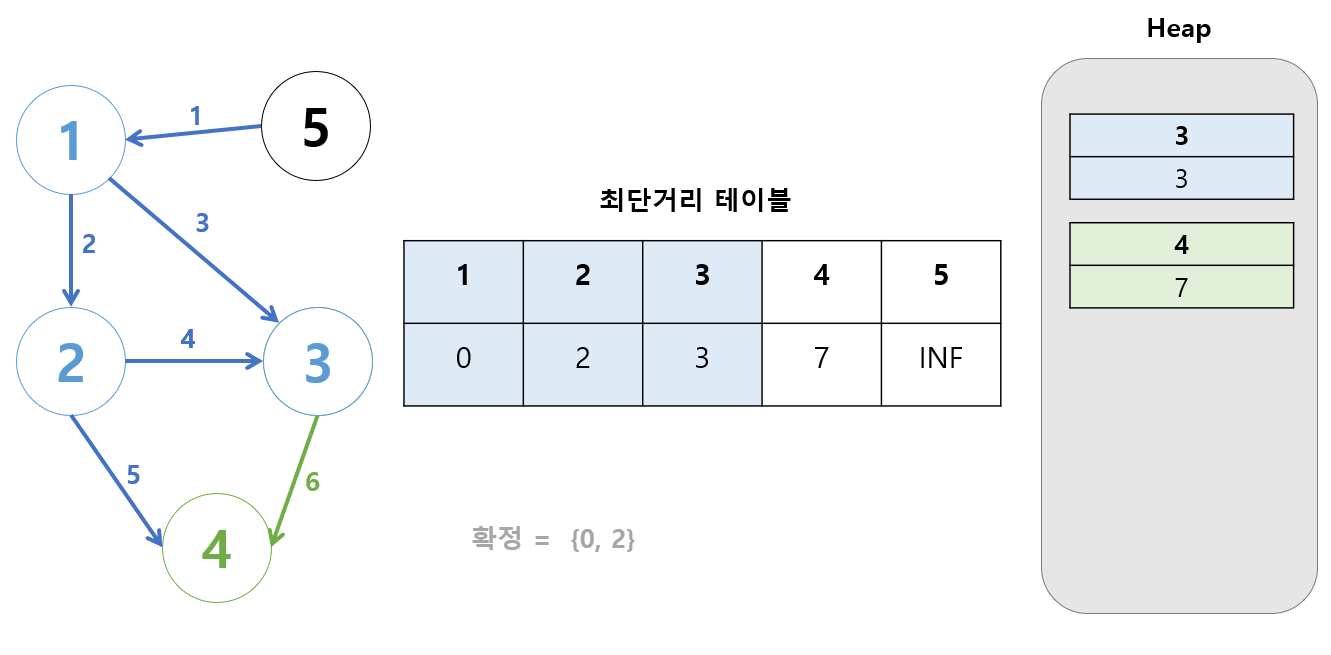
• 힙에서 거리가 가장 작은 값을 꺼낸다.
  [4, 7]이 제일 작다.
• 최단거리 테이블[4] = 7이 맞나?
  맞으므로 과정을 이어나간다.

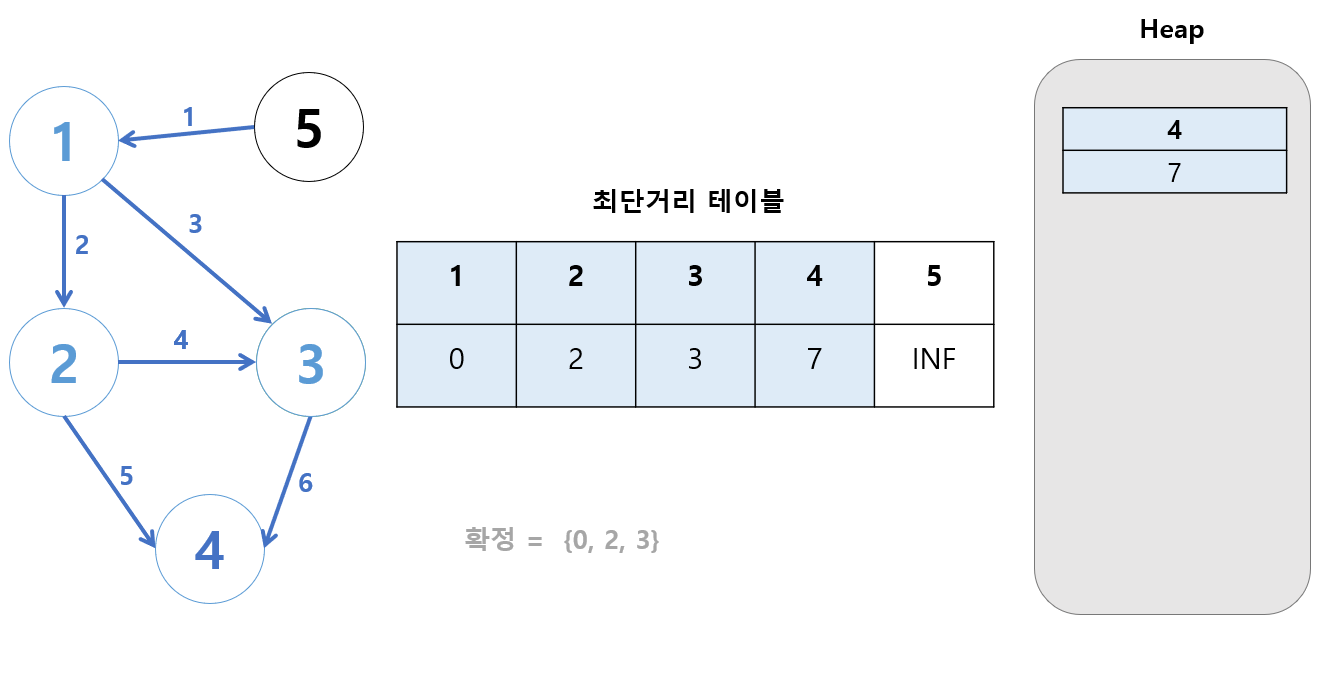
4번 정점을 거쳐 갈 수 있는 정점을 계산한다.

• 없다.

과정을 거칠게 없으므로(..) 무시한다.
처리가 끝났으므로 [4, 7]을 제거한다.

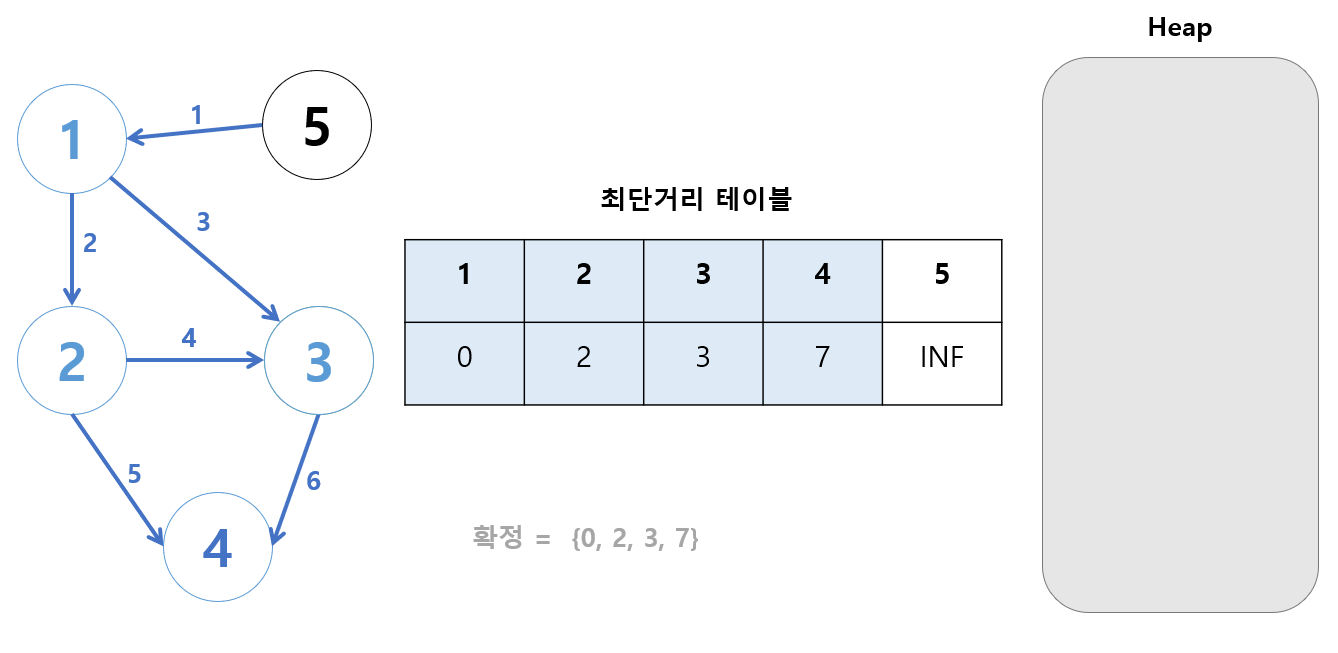
힙이 비었으므로 과정이 종료된다.
이로서 최종 최단거리 테이블은 다음과 같이 계산된다.

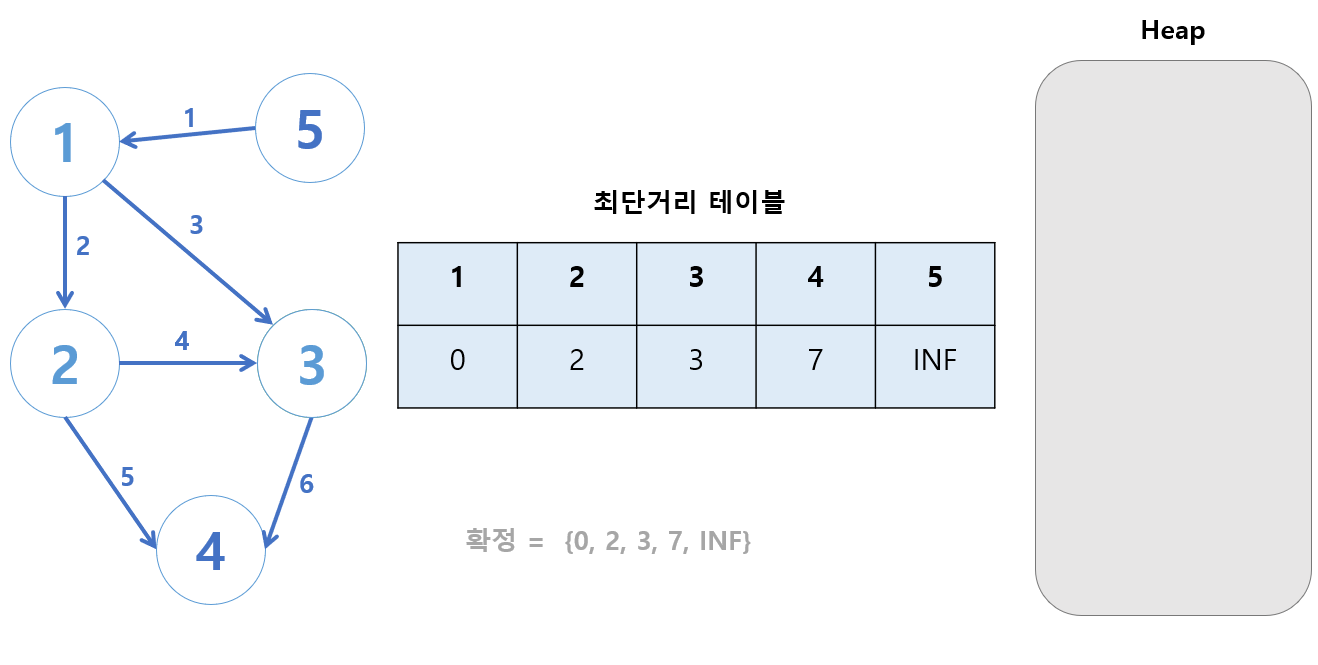
각 간선당 최대 1개의 원소가 힙에 들어간다.

• 힙의 삽입 연산: 최대 E번
• 삭제 연산: 최대 E번

따라서 시간복잡도는 O(ElogE)가 된다.

🖐🏻 그럼 힙을 구현할 줄 알아야 하나?

당연하다..

(다른 언어는 잘 모르지만)자바스크립트에서 지원하는 힙 클래스는 없는 것 같다.

그래서 다음엔 힙 알고리즘 공부와 자바스크립트로 힙을 구현하는 걸 공부할 것이다 !