[코딩테스트]백준 - 계단오르기

백준.. 친해지기 어려워 (┬┬﹏┬┬)

계단 오르기

문제

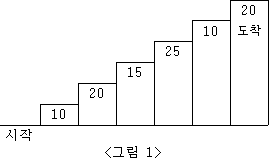
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.

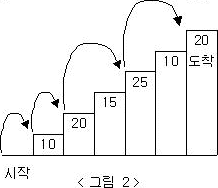
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.

계단 오르는 데는 다음과 같은 규칙이 있다.

• 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
• 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
• 마지막 도착 계단은 반드시 밟아야 한다.
• 따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다.
• 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.

각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.

입력

입력의 첫째 줄에 계단의 개수가 주어진다.

둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.

출력

첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.

예제 입력 1

6
10
20
15
25
10
20

예제 출력 1

75

출처

Olympiad > 한국정보올림피아드 > 한국정보올림피아드시․도지역본선 > 지역본선 2006 > 초등부 4번

• 문제의 오타를 찾은 사람: cjswodmlskfk eric00513

알고리즘 분류

• 다이나믹 프로그래밍

해결한 코드

// 입력받기
var fs = require('fs');
var input = fs.readFileSync('/dev/stdin').toString().split('\n');    
// input으로 들어온 입력값을 정수형으로 바꿔주기 
var n = parseInt(input[0])
for(var j=0; j<input.length; j++){
    input[j] = parseInt(input[j])
}
// 본 코드
var dp = new Array(n).fill(0)
var stairs = []
stairs = input.slice(1, input.length)
dp[0] = stairs[0]
dp[1] = Math.max(stairs[0]+stairs[1], stairs[1])
dp[2] = Math.max(stairs[0]+stairs[2], stairs[1]+stairs[2])
for(var i=3; i<n; i++){
    dp[i] = Math.max(dp[i-2]+stairs[i], dp[i-3]+stairs[i-1]+stairs[i])
}
console.log(dp[n-1])

알고리즘

어떻게 계단에 오르면 최댓값인지 계산하고 이를 dp 배열에 넣기.
※ 개인적으로 한번에 이해되지 않았다. 차근차근 짚어보도록 한다.

1. ex. stairs = [10, 20, 15, 25, 10, 20]
   맨 첫번째 계단[10]에 도달하는 최댓값은 계산할 것 없이 10.
   dp = [10]

2. 두번째 계단[20]에 도달하는 최댓값은
   ⓐ 10 + 20 (첫번째, 두번째 차곡차곡)
   ⓑ 20 (한번에 두번째 계단으로)
   이 중 큰 값 ⓐ이다.
   dp[10, 30]

3. 세번째 계단[15]에 도달하는 최댓값은
   ⓐ 10 + 15 (첫번째 밟고 바로 세번째로)
   ⓑ 20 + 15 (한번에 두번째 밟고 세번째로)
   이 중 큰 값 ⓑ이다.
   dp=[10, 30, 35]

4. 네번째 계단[25]에 도달하는 최댓값은
   ⓐ 10 + 15 + 25 (첫번째 밟고 세번째 밟고 네번째로)
   ⓑ 10 + 20 + 25 (첫번째 밟고 두번째 밟고 네번째로)
   ⓒ 20 + 15 + 25 (두번째 밟고 세번째 밟고 네번째로) ← 이 경우는 연달아 세 계단을 밟으므로 안된다.
   고로 ⓐ, ⓑ 중 큰 값 ⓑ 이다.
   dp=[10, 30, 35, 55]
   그런데 '10 + 15 + 20' 와 '10 + 20 + 25' 는 어디서 많이 본 것 같다..?
   10은 1-1에서 구하여 dp[0]에 해당하는 값이고, 10+20 은 1-2에서 구하여 dp[1]에 넣은 최댓값이다.
   잘 생각해보면, 4번째 계단에 오를 수 있는 최댓값을 계산할 때
   ① 직전 계단을 밟는 경우
   ② 직전 계단을 밟지 않는 경우 ← 전전계단을 밟는 경우
   이렇게 나눠서 생각해볼 수 있다.
   그러면, ①은 직전계단의 전전계단, 다시 말하면 전전전계단의 최댓값 + 직전계단 + 4번째 계단에 오를 때의 값이고, ②는 전전계단의 최댓값 + 4번째 계단에 오를 때의 값 으로 계산할 수 있다. 둘 중 더 큰 값이 4번째 계단에 오를 수 있는 최댓값이 되는 것이다.
   따라서, ⓐ = dp[0] + stairs[2] + stairs[3], ⓑ = dp[1] + stairs[3] 로 표기할 수 있다.

5. 다섯번째 계단[10]에 도달하는 최댓값은
   ⓐ 10 + 20 + 25 + 10
   ⓑ 20 + 15 + 10
   이 되므로, '10 + 20 + 25 + 10' 와 '20 + 15 + 10' 중 큰 값을 고른다.
   dp=[10, 30, 35, 55, 65]
   그런데 10 + 20 은 1-2에서 구한 dp[2]에 해당한다.
   즉, 이 식은 dp[2] + stairs[3] + stairs[4]로 표기할 수 있다.
   마찬가지로, 20 + 15 + 10은 dp[3] + stairs[4]로 표기할 수 있다.

다시 말해, 해당 계단에 도달할 수 있는 최댓값은
ⓐ 현재 계단 + 바로 전 계단 + 전전전계단의 최댓값 = stairs[i] + stairs[i-1] + dp[i-3]
ⓑ 현재 계단 + 전전계단의 최댓값 = stairs[i] + dp[i-2]
둘 중 더 큰 값이 되는 것이다.

６. 이렇게 dp배열에 해당 계단을 오를 수 있는 최댓값의 합으로 계산되어 들어간다.
７. dp배열의 가장 마지막 원소를 출력한다.

어려웠다... ㅠ
동적 프로그래밍 쉽지 않다. 하지만 규칙 찾는 것도 나름 재미중의 하나라고 생각한다(어쩌면 노력 ㅋㅋㅋ).
이제 포도주 시식도 풀어봐야지. 동적 프로그래밍이랑 친해지고 싶다 .. 백준쓰랑도 ..