[코딩테스트]백준 - 케빈 베이컨의 6단계 법칙(1389)

문제

케빈 베이컨의 6단계 법칙(1389)

해결한 코드

var fs = require('fs');
var input = fs.readFileSync('/dev/stdin').toString().trim().split('\n');
var peopleInfo = input[0].split(' ').map((e) => +e)
var n = peopleInfo[0]
var m = peopleInfo[1]
var relationships = []
for (var i = 1; i < input.length; i++) {
    relationships.push(input[i].split(' ').map((e) => +e))
}
var floyd = setFloyd()
var answer = KevinBaconOfEach(floyd)
console.log(answer)

function initFloyd() {
    var floyd = []
    for (var i = 0; i < n; i++) {
        floyd.push(Array(n).fill(Infinity))
        floyd[i][i] = 0
    }
    for (var i = 0; i < relationships.length; i++) {
        var currentRelationship = relationships[i]
        if (floyd[currentRelationship[0] - 1][currentRelationship[1] - 1] !== 1) {
            floyd[currentRelationship[0] - 1][currentRelationship[1] - 1] = 1
            floyd[currentRelationship[1] - 1][currentRelationship[0] - 1] = 1
        }
    }
    return floyd
}

function setFloyd() {
    var floyd = initFloyd()
    for (var i = 0; i < n; i++) {
        for (var s = 0; s < n; s++) {
            if (s === i) continue
            for (var d = 0; d < n; d++) {
                if (floyd[s][i] !== Infinity && floyd[i][d] !== Infinity && floyd[s][d] > floyd[s][i] + floyd[i][d]) {
                    floyd[s][d] = floyd[s][i] + floyd[i][d]
                }
            }
        }
    }
    return floyd
}

function KevinBaconOfEach(floyd) {
    var sum = floyd[0].reduce((a, b) => a + b)
    var min = sum
    var index = 0
    for (var i = 1; i < floyd.length; i++) {
        sum = floyd[i].reduce((a, b) => a + b)
        if(sum < min){
            min = sum
            index = i
        }
    }
    return index+1
}

풀이

※ 플로이드 와샬 알고리즘으로 푼다.

1. 플로이드 그래프를 만든다.

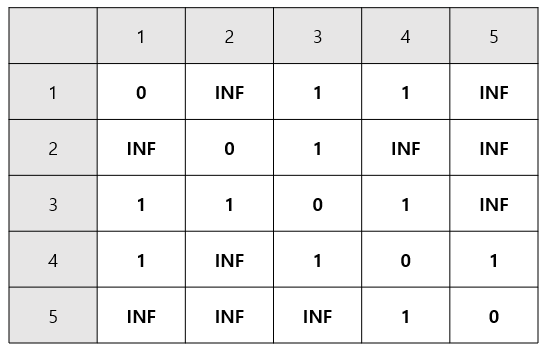
예를들어 다섯 사람의 친구관계에 대한 정보가 다음과 같이 입력된다면,

relationships = [ 
  [ 1, 3 ], 
  [ 1, 4 ], 
  [ 4, 5 ], 
  [ 4, 3 ], 
  [ 3, 2 ] 
]

이는 누군가를 거치지 않고 바로 이어진 친구관계라는 의미이다.
1~5의 관계에 대해 다음과 같은 그림으로 나타낼 수 있다.

• 자기 자신은 단계를 거치지 않으므로 0으로,
• 입력으로 들어온 친구관계는 1단계라고 할 수 있으므로, 1로 표기한다.
• 나머지는 바로 이어지지 않았으니 무한대 값을 주어

초기 플로이드 그래프를 완성한다.
※ 입력으로 들어오는 친구관계에 중복이 있을 수 있다고 하였으므로, 이미 관계값이 1이면 건너뛴다.

2. 플로이드 와샬 알고리즘으로 플로이드 그래프를 세팅한다.

플로이드 와샬 알고리즘의 베이스는
시작정점이 s, 도착정점이 d, 중간에 거치는 정점이 i라면

floyd[s][d] = min(floyd[s][d], floyd[s][i] + floyd[i][d])

가 된다는 것이다.
이를 활용하여 INF에 해당하는 값을 계산해준다.

2-1. s -> d를 갈 때, 1을 거친다면?

• 2 -> 1은 INF, 즉 친구관계가 아니므로 거칠 수 없다.
• 3 -> 1은 친구관계다.
  • 3 -> 1 -> 4 로 4까지 2 단계를 거치면 되는데..
    3 -> 4 는 1단계로 바로 거칠 수 있다. 굳이 2단계나 안거쳐도 된다.
• 4 -> 1은 친구관계다.
  • 4 -> 1 -> 3 으로 2 단계를 거치면 되지만, 위와 같이 1단계로 바로 거칠 수 있으므로 패스한다.
• 5 -> 1은 INF, 즉 친구관계가 아니므로 거칠 수 없다.

따라서, 위 계산 결과를 반영하면,

그대로다.

2-2. s -> d를 갈때, 2를 거친다면?

• 1 -> 2는 INF이므로 거칠 수 없다.
• 3 -> 2는 친구관계다.
  • 3 -> 2 -> ... 거칠 수 있을 만한 친구가 없다.
• 4, 5도 INF이므로 거칠 수 없다.

2-3. s -> d를 갈때, 3을 거친다면?

• 1 -> 3은 친구관계다.
  • 1 -> 3 -> 2로, 2까지 2 단계 거치면 된다.
  • 1 -> 3 -> 4로, 4까지 1 + 2 단계 거치면 되긴 하는데...
    1 -> 4은 1단계로 바로 거칠 수 있다. 즉, 3단계까지 안거쳐도 된다.
    따라서 1 -> 4 는 1 단계 거치는 걸로 둔다.
• 2 -> 3은 친구관계다.
  • 2 -> 3 -> 1로, 1까지 2 단계 거치면 된다.
  • 2 -> 3 -> 4로, 4까지 1 + 2 단계 거치면 된다.
• 4 -> 3은 친구관계다.
  • 4 -> 3 -> 2로, 2까지 2 + 1단계 거치면 된다.

즉, 플로이드 와샬 알고리즘을 통해 친구관계를 계산할 때
✔ 중간에 거치는 i와 친구인지
✔ i를 거치는게 더 작은지
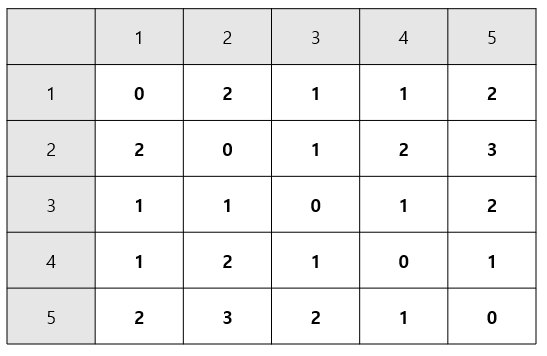
를 확인하여 친구관계를 계산한다.

이런식으로 4, 5를 거치는 것까지 플로이드 와샬 알고리즘을 돌려 플로이드 그래프를 완성하면,

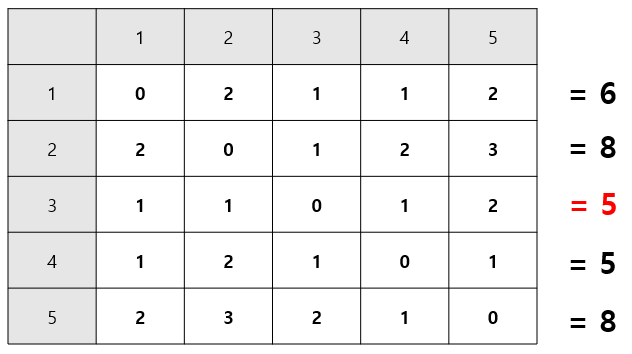
이러한 형태가 나온다.

3. 각 행별로 케빈 베이컨 수를 계산한다.

이렇게 각 행별로 케빈 베이컨 수를 구하여 최솟값을 가진 사람을 찾는다.
👉🏻 최솟값을 가진 사람이 여러명 있을 땐, 수가 더 빠른 사람을 출력한다.