몇개의 문제들을 풀어봤지만 그래프관련 문제들은 여전히 오래 생각하고 오래 푸는거 같다..
플로이드 2
관련문제 - 플로이드
문제
n(1≤n≤100)개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 m(1≤m≤100,000)개의 버스가 있다. 각 버스는 한 번 사용할 때 필요한 비용이 있다.
모든 도시의 쌍 (A, B)에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 도시의 개수 n(1≤n≤100)이 주어지고 둘째 줄에는 버스의 개수 m(1≤m≤100,000)이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다.
출력
먼저, N개의 줄을 출력해야 한다. i번째 줄에 출력하는 j번째 숫자는 도시 i에서 j로 가는데 필요한 최소 비용이다. 만약, i에서 j로 갈 수 없는 경우에는 그 자리에 0을 출력한다.
그 다음에는 NN개의 줄을 출력해야 한다. iN+j번째 줄에는 도시 i에서 도시 j로 가는 최소 비용에 포함되어 있는 도시의 개수 K를 출력한다. 그 다음, 도시 i에서 도시 j로 가는 경로를 공백으로 구분해 출력한다. 이때, 도시 i와 도시 j도 출력해야 한다. 만약, i에서 j로 갈 수 없는 경우에는 0을 출력한다.
예제 입력 1
5 14 1 2 2 1 3 3 1 4 1 1 5 10 2 4 2 3 4 1 3 5 1 4 5 3 3 5 10 3 1 8 1 4 2 5 1 7 3 4 2 5 2 4예제 출력 1
0 2 3 1 4 12 0 15 2 5 8 5 0 1 1 10 7 13 0 3 7 4 10 6 0 0 2 1 2 2 1 3 2 1 4 3 1 3 5 4 2 4 5 1 0 5 2 4 5 1 3 2 2 4 3 2 4 5 2 3 1 3 3 5 2 0 2 3 4 2 3 5 3 4 5 1 3 4 5 2 4 4 5 1 3 0 2 4 5 2 5 1 2 5 2 3 5 1 3 3 5 2 4 0출처
- 문제를 만든 사람: baekjoon
해결한 코드
var fs = require('fs');
var input = fs.readFileSync('/dev/stdin').toString().trim().split('\n');
var n = input[0] / 1
var m = input[1] / 1
var busRoutes = []
for (var i = 2; i < input.length; i++) {
busRoutes.push(input[i].split(' ').map((element) => element / 1))
}
var max = 1000001
function setEmptyGraph() {
var graph = []
for (var i = 0; i < n; i++) {
graph.push(Array(n).fill(max))
graph[i][i] = 0
}
return graph
}
function createNxtGraph() { // 경로복원을 위한 nxtGraph 만들기
var graph = []
for (var i = 0; i < n; i++) {
graph.push(Array(n).fill(null))
}
return graph
}
function setInitialFloyd() {
var floydGraph = setEmptyGraph()
var nxtGraph = createNxtGraph() // 경로복원을 위한 nxtGraph
for (var i = 0; i < busRoutes.length; i++) {
var departure = busRoutes[i][0]
var arrival = busRoutes[i][1]
var busRoute = busRoutes[i][2]
if (busRoute < floydGraph[departure - 1][arrival - 1]) {
floydGraph[departure - 1][arrival - 1] = busRoute
nxtGraph[departure - 1][arrival - 1] = arrival - 1
}
}
return [floydGraph, nxtGraph]
}
function findAnswerWithFloyd(Graphs) {
var floydGraph = Graphs[0]
var nxtGraph = Graphs[1]
for (var i = 0; i < floydGraph.length; i++) {
for (var j = 0; j < floydGraph.length; j++) {
if (j === i) continue
else {
for (var k = 0; k < n; k++) {
if (floydGraph[j][i] !== max && floydGraph[i][k] !== max) {
var floydBusRoute = floydGraph[j][i] + floydGraph[i][k]
if (floydBusRoute < floydGraph[j][k]) {
floydGraph[j][k] = floydBusRoute
nxtGraph[j][k] = nxtGraph[j][i] // 경로 기록
}
}
}
}
}
}
return [floydGraph, nxtGraph]
}
function trackPaths(nxtGraph) { // 경로 추적하기
var element = [] // 경로 저장
var result = []
for (var i = 0; i < nxtGraph.length; i++) {
for (var j = 0; j < n; j++) {
var currentVertex = nxtGraph[i][j]
if (currentVertex === null) { // i -> i (자기 자신)의 경우
element = [0]
} else if (currentVertex === j) { // 중간 정점 없이 한번에 도착
element = []
element.push(i + 1, currentVertex + 1) // 도시 저장
} else { // 중간 정점이 있는 경우
element = []
element.push(i + 1)
while (true) {
if(currentVertex === j){ // 도착점에 도달하면
element.push(currentVertex + 1)
break;
}
element.push(currentVertex + 1) // 경로 저장
currentVertex = nxtGraph[currentVertex][j] // 도착점을 향해 가기
}
}
result.push(element)
}
}
return result
}
function changeMaxtoZero(Graphs) {
var floydGraph = Graphs[0]
var nxtGraph = Graphs[1]
for (var i = 0; i < floydGraph.length; i++) {
for (var j = 0; j < n; j++) {
if (floydGraph[i][j] === max) floydGraph[i][j] = 0
}
}
return [floydGraph, nxtGraph]
}
if (n === 1) {
console.log(0)
} else {
var Graphs = setInitialFloyd()
Graphs = findAnswerWithFloyd(Graphs)
Graphs = changeMaxtoZero(Graphs)
var floydGraph = Graphs[0]
var nxtGraph = Graphs[1]
var nxtGraphResult = trackPaths(nxtGraph)
print(floydGraph, nxtGraphResult)
}
function print(floydGraph, nxtGraphResult) {
var answer = ''
var count = 0
// 최소 비용 출력하기
for (var i = 0; i < floydGraph.length; i++) {
answer += floydGraph[i].join(' ') + '\n'
}
// 그 다음으로 경로 출력하기
for (var i = 0; i < nxtGraphResult.length; i++) {
if (nxtGraphResult[i].length === 1 && nxtGraphResult[i][0] === 0) {
answer += '0' + '\n'
continue
}
count = nxtGraphResult[i].length // 도시 갯수
answer += count + " " + nxtGraphResult[i].join(' ') + '\n'
}
console.log(answer.trim())
}풀이
- 플로이드 문제에서 경로복원 부분을 추가하였다.
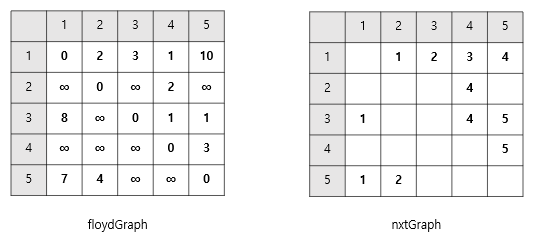
1. 경로를 기록하기 위한 배열을 만든다.
floydGraph는 플로이드 문제에서 구현한 그래프이다.
nxtGraph는 경로를 기록하기 위해 만든 배열이다.
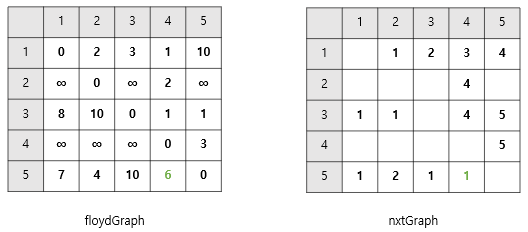
nxtGraph의 초기 상태로 i에서 j로 단번에 갈수 있는 경우에만nxtGraph[i][j] = j로 하였다.2. 플로이드 그래프의 값이 바뀔 때마다 경로를 새로 기록한다.
ex. 1을 경유해서 비용이 더 작아진 경우를 먼저 살펴보면,
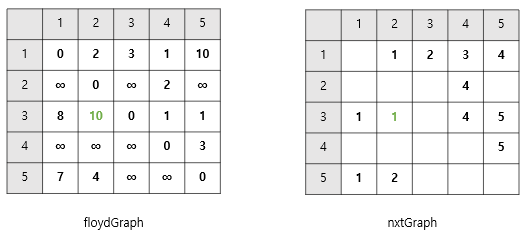
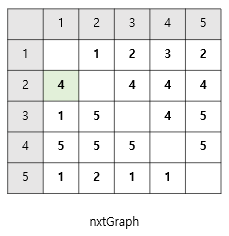
- 3 -> 2로 가는 경우, 3 -> 1 -> 2로 갈때 비용이 더 적었다.
floydGraph[3][2]의 값이floydGraph[3][1]+floydGraph[1][2]로 바뀌었으니
👉🏻nxtGraph[3][2]를nxtGraph는[3][1]의 값으로 바꿔준다.
1을 경유했음을 기록하는 것이다.
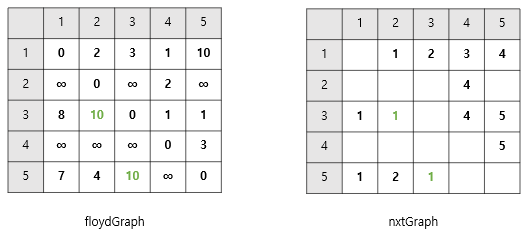
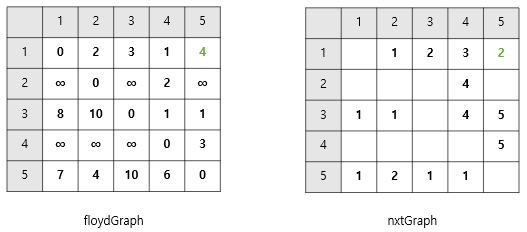
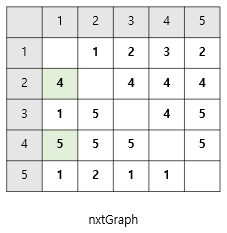
- 5 -> 3으로 가는 경우, 5 -> 1 -> 3으로 갈때 비용이 더 적었다.
floydGraph[5][3]의 값이floydGraph[5][1]+floydGraph[1][3]로 바뀌었으니
👉🏻nxtGraph[5][3]를nxtGraph는[5][1]의 값으로 바꿔준다.
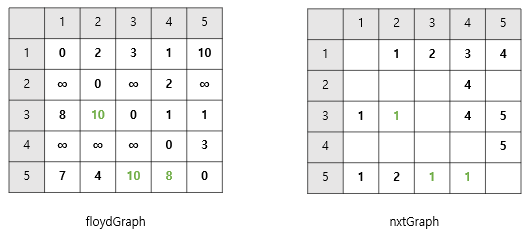
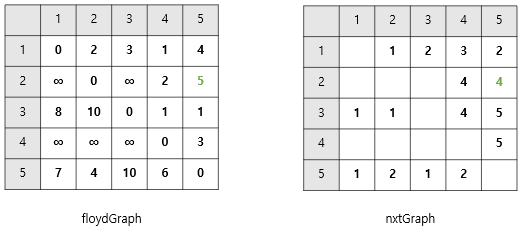
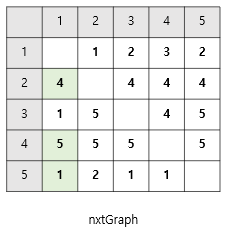
- 5 -> 4로 가는 경우, 5 -> 1 -> 4로 갈 때 비용이 더 적었다.
floydGraph[5][4]의 값이floydGraph[5][1]+floydGraph[1][4]로 바뀌었으니
👉🏻nxtGraph[5][4]를nxtGraph는[5][1]의 값으로 바꿔준다.
즉, 시작 점을 s, 도착점을 d라고 한다면,
floydGraph[s][d]의 값이floydGraph[s][1]+floydGraph[1][d]로 바뀌었을 때
👉🏻nxtGraph[s][d]를nxtGraph는[s][1]로 바꿔준다.
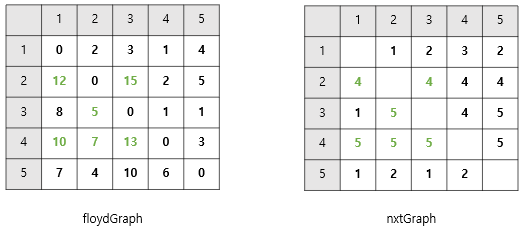
- 2를 경유할 때
- 3을 경유할 때
- 4를 경유할 때
- 5를 경유할 때
3. 경로를 탐색한다.
예를 들어 2 -> 1 의 경로를 살펴보자.
nxtGraph[2][1]는?
4 이므로, 이제nxtGraph[4][1]로 간다.
5 이므로, 이제nxtGraph[5][1]로 간다.
1이다. 도착했다.
이를 통해 2 -> 4 -> 5 -> 1 로 갔음을 알 수 있다.4. 플로이드 그래프와 탐색한 경로를 출력한다.
출력 조건에 맞게
도시 개수, 시작 도시, 중간 도시 ,도착 도시에 맞춰 출력한다.