.png)
플로이드
문제
n(1 ≤ n ≤ 100)개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 m(1 ≤ m ≤ 100,000)개의 버스가 있다. 각 버스는 한 번 사용할 때 필요한 비용이 있다.
모든 도시의 쌍 (A, B)에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 도시의 개수 n(1 ≤ n ≤ 100)이 주어지고 둘째 줄에는 버스의 개수 m(1 ≤ m ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다.
시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다.
출력
n개의 줄을 출력해야 한다. i번째 줄에 출력하는 j번째 숫자는 도시 i에서 j로 가는데 필요한 최소 비용이다. 만약, i에서 j로 갈 수 없는 경우에는 그 자리에 0을 출력한다.
예제 입력 1
5 14 1 2 2 1 3 3 1 4 1 1 5 10 2 4 2 3 4 1 3 5 1 4 5 3 3 5 10 3 1 8 1 4 2 5 1 7 3 4 2 5 2 4예제 출력 1
0 2 3 1 4 12 0 15 2 5 8 5 0 1 1 10 7 13 0 3 7 4 10 6 0출처
- 문제의 오타를 찾은 사람: algoshipda
- 문제를 만든 사람: baekjoon
- 빠진 조건을 찾은 사람: dbfldkfdbgml koosaga
- 데이터를 추가한 사람: dlwocks31 kyaryunha_cpp
알고리즘 분류
- 플로이드 와샬 알고리즘
- 그래프 이론
해결한 코드
var fs = require('fs');
var input = fs.readFileSync('/dev/stdin').toString().trim().split('\n');
var n = input[0] / 1
var m = input[1] / 1
var busRoutes = []
for (var i = 2; i < input.length; i++) {
busRoutes.push(input[i].split(' ').map((element) => element / 1))
}
var max = 10000001
function setEmptyGraph() { // 초기 그래프 만들기
var graph = []
for (var i = 0; i < n; i++) {
graph.push(Array(n).fill(max))
graph[i][i] = 0 // 자기 자신은 0
}
return graph
}
function setInitialFloyd() { // 초기 플로이드 그래프 만들기
var floydGraph = setEmptyGraph()
for (var i = 0; i < busRoutes.length; i++) {
var departure = busRoutes[i][0]
var arrival = busRoutes[i][1]
var busRoute = busRoutes[i][2]
if (busRoute < floydGraph[departure - 1][arrival - 1]) {
floydGraph[departure - 1][arrival - 1] = busRoute
}
}
return floydGraph
}
function findAnswerWithFloyd(floydGraph) { // (최단거리) 플로이드 그래프 만들기
var floydBusRoute = 0
for (var i = 0; i < floydGraph.length; i++) {
for (var j = 0; j < floydGraph.length; j++) {
if (j === i) continue
else {
for (var k = 0; k < n; k++) {
if(floydGraph[j][i] !== max && floydGraph[i][k] !== max){
floydBusRoute = floydGraph[j][i] + floydGraph[i][k]
if (floydBusRoute < floydGraph[j][k]) {
floydGraph[j][k] = floydBusRoute
}
}
}
}
}
}
return floydGraph
}
function changeMaxtoZero(floydGraph){ // 갈 수 없는 곳은 0으로 세팅
for(var i=0; i<floydGraph.length; i++){
for(var j=0; j<n; j++){
if(floydGraph[i][j] === max) floydGraph[i][j] = 0
}
}
return floydGraph
}
function print(floydGraph){ // 답 출력하기
var answer = ''
for(var i=0; i<floydGraph.length; i++){
answer += floydGraph[i].join(' ') + '\n'
}
console.log(answer.trim())
}
var floydGraph = setInitialFloyd()
floydGraph = findAnswerWithFloyd(floydGraph)
floydGraph = changeMaxtoZero(floydGraph)
print(floydGraph)풀이
※ 플로이드 와샬 알고리즘을 사용하였다.
1. 그래프 파악하기
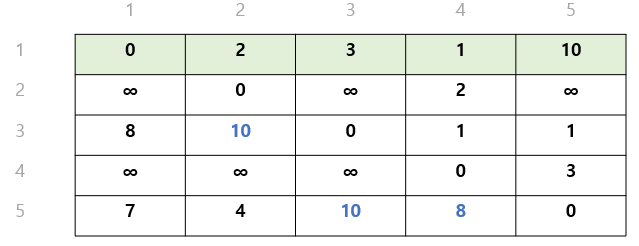
입력으로 들어온 값들을 예로 들면, 다음과 같은 그래프를 그릴 수 있다.
이를 표로 표현하면,
이렇게 표현될 수 있다.
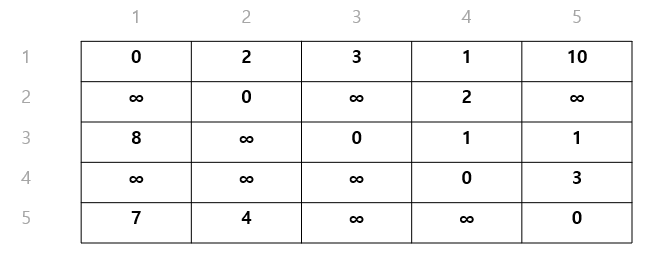
각 정점을 "단번에" 갈 수 있는 비용만 표시했다.
이를 (코드상에서) 2차원 배열 방식으로 작성하려면,[ [ 0, 2, 3, 1, 10 ], [ 1000001, 0, 1000001, 2, 1000001 ], [ 8, 1000001, 0, 1, 1 ], [ 1000001, 1000001, 1000001, 0, 3 ], [ 7, 4, 1000001, 1000001, 0 ] ]이렇게 작성하게 된다. 무한대에 해당하는 값은 계산할 수 있는 비용보다 더 큰 값으로 설정해놓는다.
2. 플로이드 워샬 알고리즘을 사용하여 그래프를 계산한다.
위와같이 초기 그래프를 완성하였다면, 이제는 최단거리를 찾기 위한 플로이드 와샬 계산을 해야 한다.
2-1. 정점으로부터 1을 거쳐 가면 비용이 얼마나 드나?
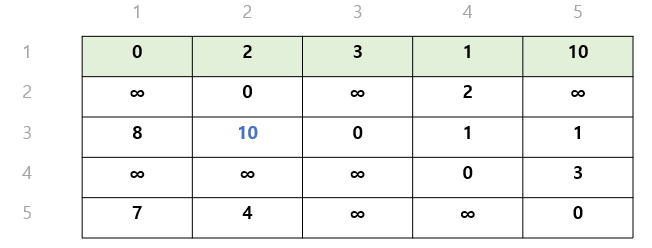
✔ 정점 2에서 3, 4, 5를 갈 때, 1을 거쳐 가면 비용이 어떻게 되나 살펴보자.
👉🏻 2 -> 1로 가는 길은 ∞ 이다. 갈 수 없으므로 3부터 시작해보자...✔ 정점 3에서 2, 4, 5를 1을 거쳐 가면 비용이 어떻게 되나?
- 현재 3->2 : ∞
3 -> 1 -> 2 : 8 + 2 = 10
10이 더 작으므로, 그래프[3][2] = 10으로 변경한다.- 현재 3 -> 4 : 1
3 -> 1 -> 4 : 8 + 1 = 9
1이 더 작으므로, 바꿀 필요 없다.- 현재 3 -> 5 : 1
3 -> 1 -> 5 : 8 + 10 = 18
1이 더 작으므로, 바꿀 필요 없다.
(참고) 1을 거쳐갈때를 계산한다는 의미로 초록 표시를 해두었다.
무한대의 값이 10으로 바뀌었다.즉, 시작 정점이
i이고, 도착 정점이j, 거쳐가는 정점이1이라면비용 = min(그래프[i][1] + 그래프[1][j], 그래프[i][j])가 되는 것이다.
✔ 위와 같이 4, 5도 1을 거쳐 갈때 각 정점들에 대한 비용을 계산한다.
- 1을 거쳐 갔을 때 비용이 더 작다면 그 값으로 바꾼다.
2-2. 모든 정점에 대하여 각 정점을 거쳐가면 비용이 얼마나 드는지 계산한다.
- 즉, 1에서 2, 3, 4, 5를 갈 때
- 2를 거치면?
- 3을 거치면?
- 4를 거치면?
- 5를 거치면?
을 모두 계산하며 최소 비용을 구해준다.
👉🏻 이를 n개의 정점 모두 실시한다.3. 그래프 점검을 한다.
- 플로이드와샬로 그래프를 모두 완성하였는데, 그래도 값이 여전히 무한대인 것이 있다면?
👉🏻 해당 정점은 갈 수 없다는 의미이므로, 값을 0으로 변경한다.4. 그래프를 문자열로 바꿔 출력한다.
그래프의 각 1차원 배열 원소들을 공백을 포함한 문자열로 바꿔 출력한다.
처음엔 0으로 바꿔주는 부분을 구현하지 않았고,
다음으론 max값을 작게해서 몇번의 실패를 맛보았다...
98%에서 실패한다면, 0을 바꿔주는 부분을 빼먹었거나 max값을 작게 하지 않았는지를 생각해보면 좋을 것 같다.
참고로 max값은 (버스) 100,000 × (도시) 100을 곱한 값보다 커야 한다.
.png)
.png)
.png)