💻Greedy Algorithm
: 그리디 알고리즘은 최적화 문제를 해결하는 알고리즘이다.
: 입력 데이터 간의 관계를 고려하지 않고 수행과정에서 '욕심내어' 최소값 또는 최대값을 가진 데이터를 선택한다. (근시안적인 선택)
: 매 수행 과정마다 최적의 값을 선택하기 때문에 최종 결과가 최적해가 아닐 수 있다.
🧐Greedy algorithm 사용 이유
✏️Submodularity
: Diminishing returns
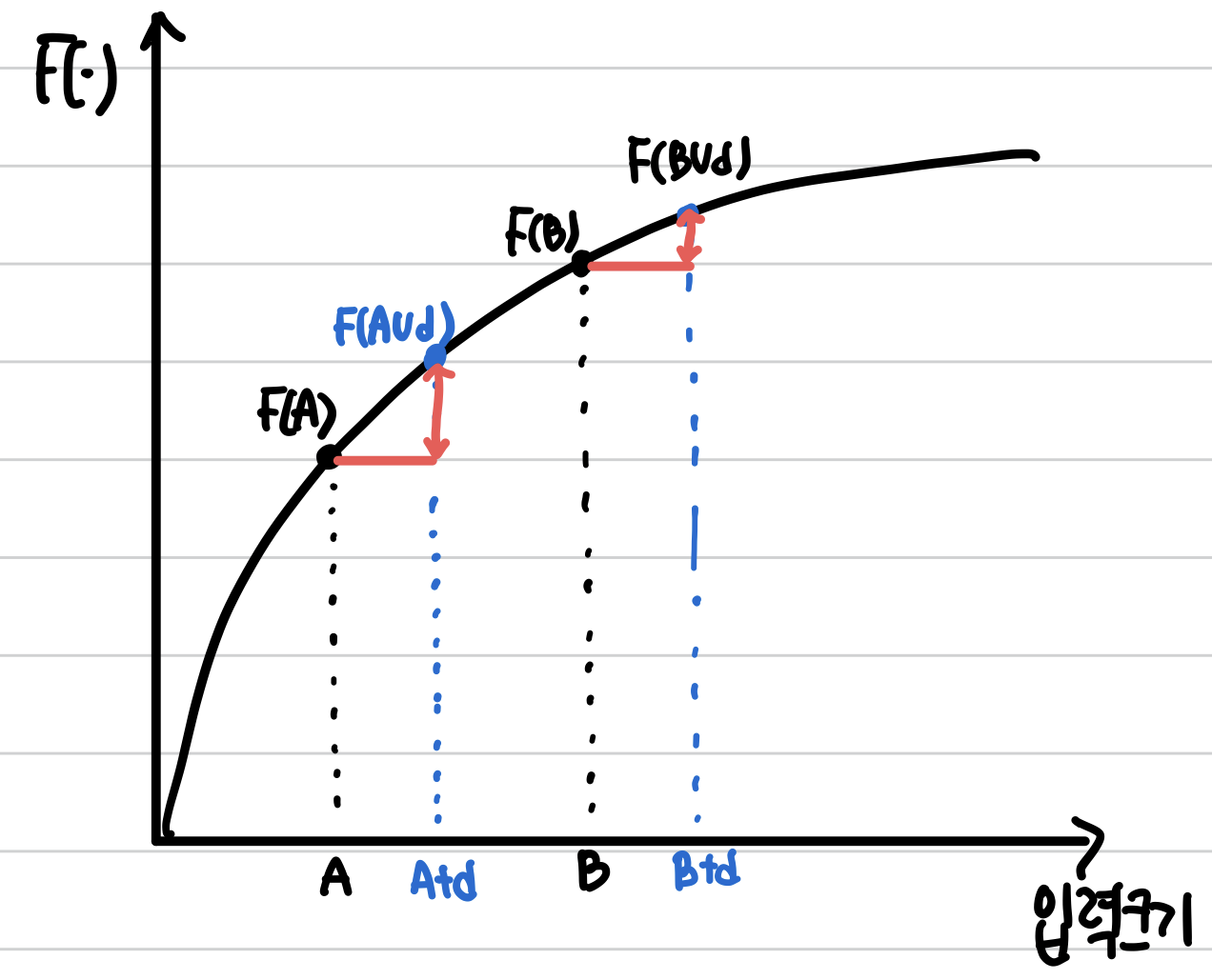
F(A + d ) - F(A) >= F(B + d)-F(B)
풀고자 하는 문제가 Submodularity라면 Greedy 사용 시 최소 성능 (1-e^(-1))을 보장한다.
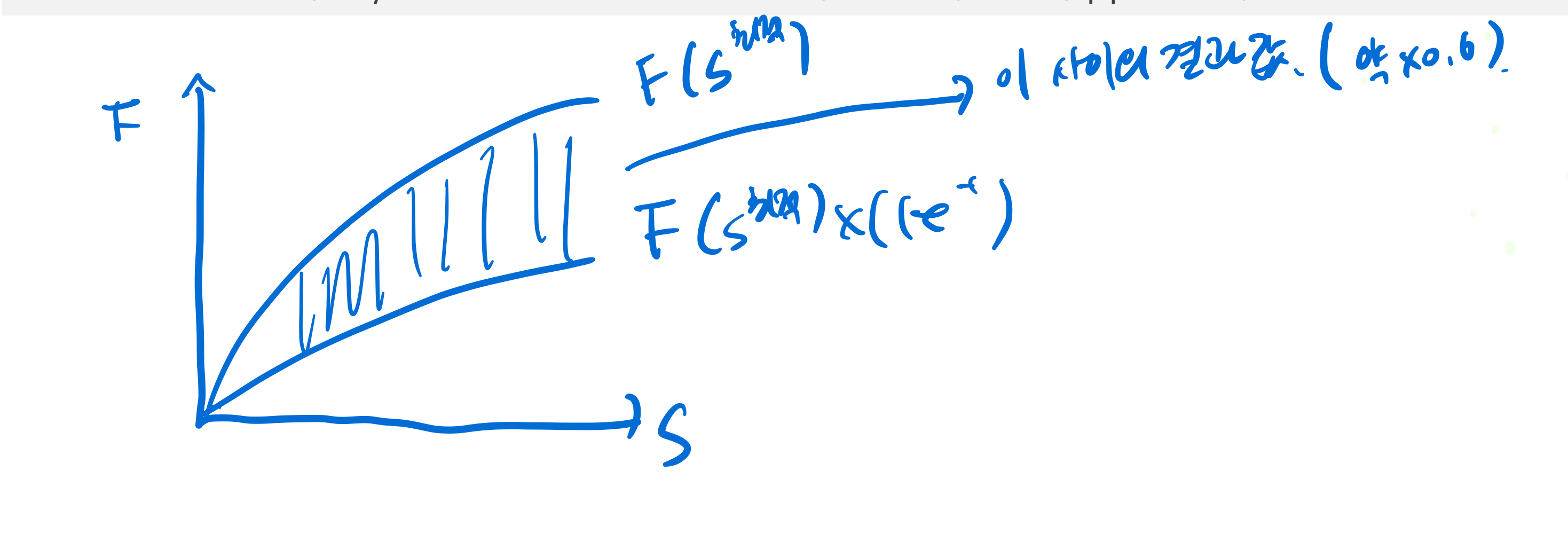
📎1. 동전 거스름돈 문제 (Coin Change)
: 남은 액수를 초과하지 않는 조건하에 '욕심내어' 가장 큰 액면의 동전을 취한다.
-> 최적해가 아닐 수 있다. (입력 데이터와 액면가에 따라 변화)
📎2. 최소 신장 트리(Minimun Spanning Tree)
: 주어진 가중치 그래프에서 사이클이 없이 모든 점들을 연결시킨 트리들 중 간선들의 가중치 합이 최소인 트리
: 그래프의 점의 수가 n일 때, 신장 트리에는 (n-1)개의 간선이 있다.
: 트리에 간선을 하나 추가시키면, 반드시 사이클이 만들어진다.
- Kruskal algorithm
: 가중치가 가장 작은 간선이 사이클을 만들지 않을 때에만 '욕심내어' 그 간선을 추가시킨다. - Prim algorithm
: 임의의 점 하나를 선택한 후, (n-1)개의 간선을 하나씩 추가시켜 트리를 만든다.
📎2-1. Kruskal algorithm
✏️수행과정
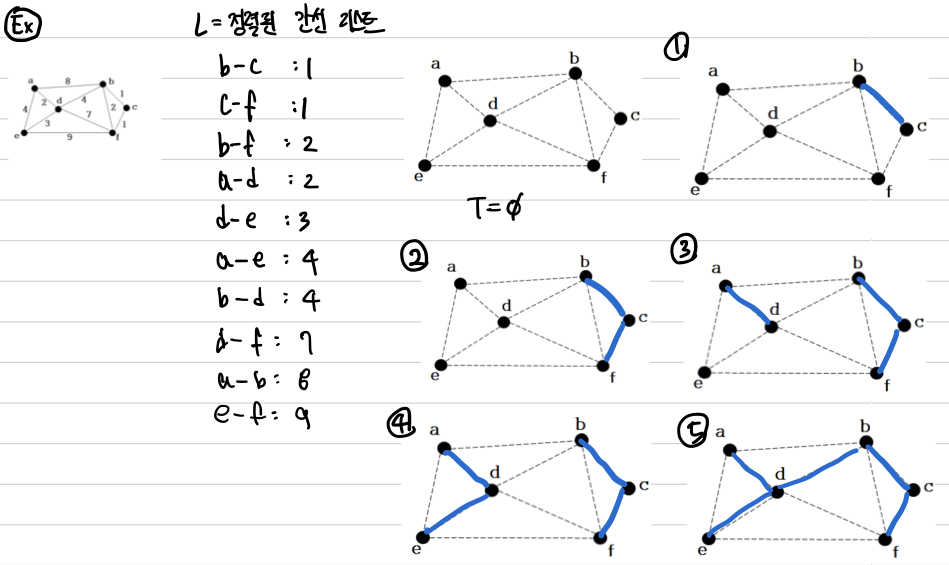
- 그래프의 간선을 오름차순으로 정렬한 후 L에 저장한다.
- L의 앞에 있는 간선 부터 선택하고 L에서 해당 간선을 제거하고, 간선을 트리에 추가시킨다. 이때, 선택한 간선이 사이클을 만들면 선택하지 않는다. 이 과정을 반복한다.
시간복잡도 : O(mlogm) (간선 정렬) + O (log * m) (사이클 검사)
= O(mlogm)
📎2-2. Prim algorithm
: 어떤 임의의 점을 선택하냐에 따라 결과가 달라질 수 있다.
✏️수행과정
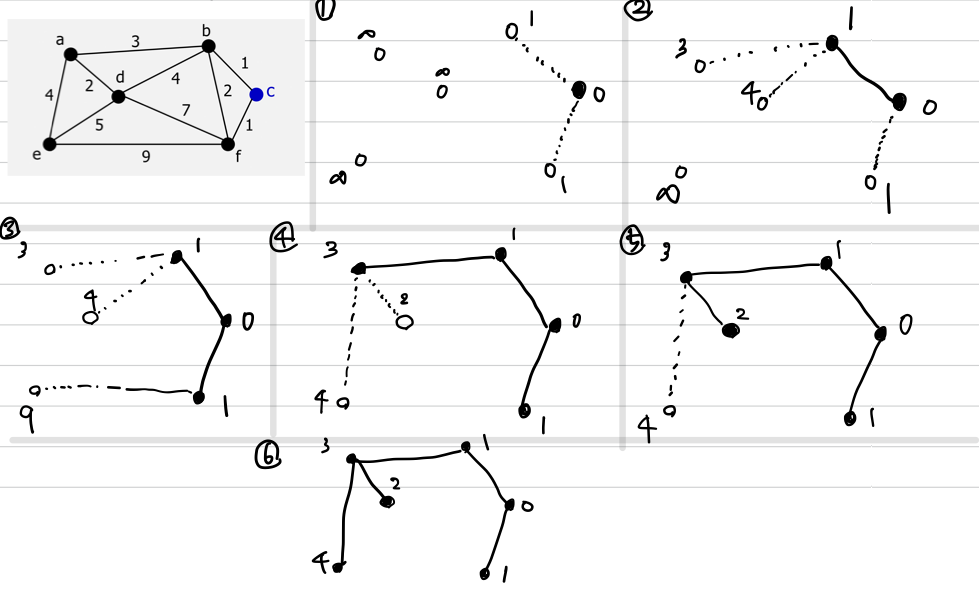
- 그래프에서 임의의 점을 선택한다. ( c 를 선택 )
- c와 연결된 점들에 대해 간선의 가중치를 저장해 놓는다. (나머지는 ∞로 초기화 - 선택하지 않기 위해서)
- 저장된 가중치 중 최소인 간선의 가중치를 선택하고 간선을 추가한다.
- 추가된 점에 대해 간선의 가중치를 업데이트 하고 위의 과정을 반복한다.
시간복잡도: O(n^2)
Binary Heap을 사용하면 시간복잡도가 감소한다.
📎3. Dijkstra algorithm
: 하나의 정점에서 다른 모든 정점으로 가는 최단경로를 알고 싶을 때 사용한다.
✏️수행과정
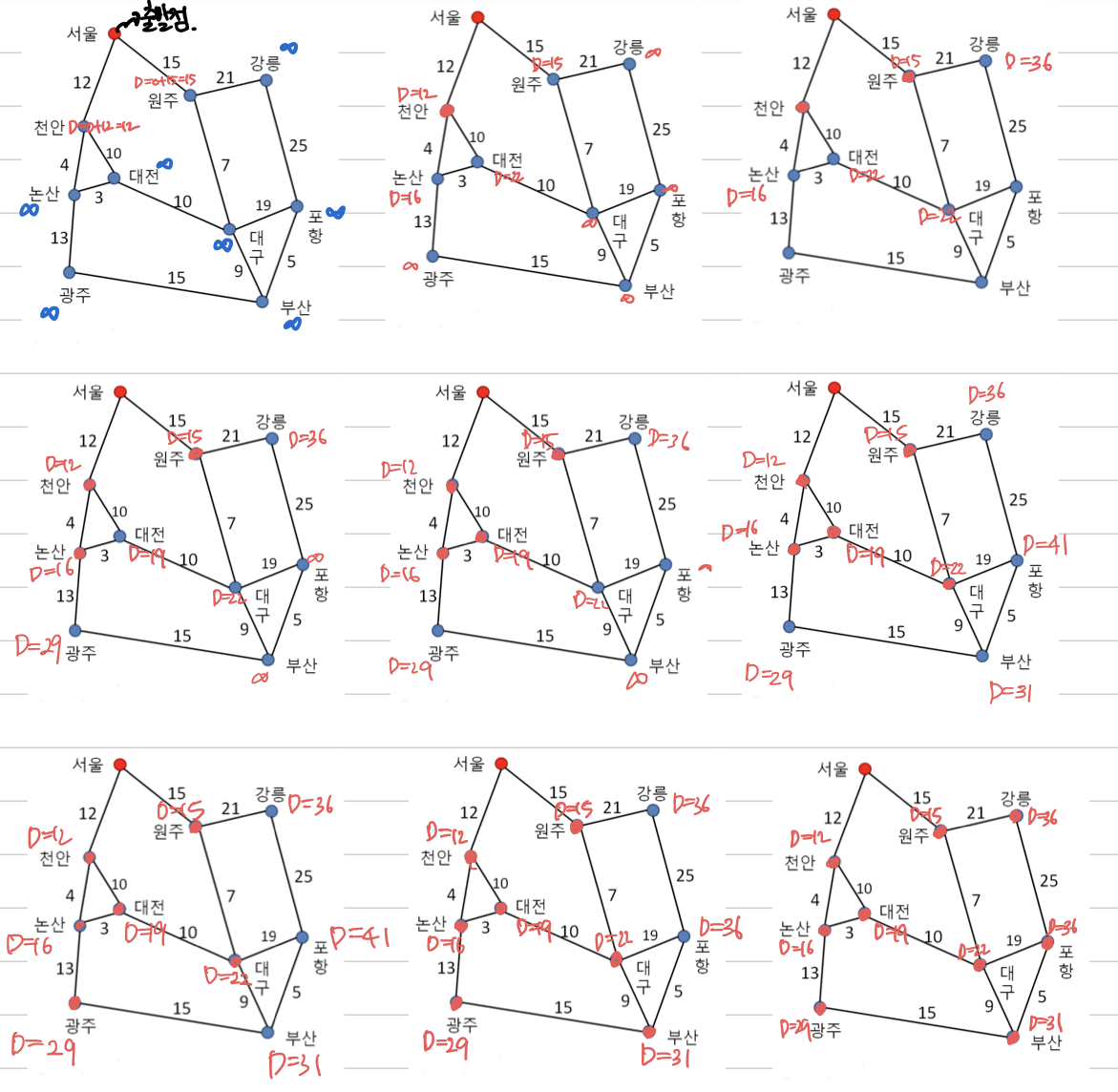
-
확정된 점은 빨간색, 확정되지 않은 점은 파란색으로 표시했다.
-
간선 완화(Edge Relaxation) : 최신으로 선택한 점을 경유해 가중치가 감소한다면 그 점의 가중치를 갱신한다.
시간복잡도: O(n^2)
Binary Heap 사용 시 O(mlogm)