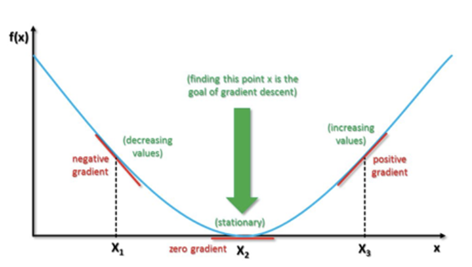
경사하강법?

경사 하강법은 1차 근삿값 발견용 최적화 알고리즘이자 최적화 이론의 한 방법입니다.
기본 개념은 함수의 기울기를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이며, 딥러닝에서 경사하강법이 자주 사용됩니다.
함수 f(x)에서 경사를 따라 여러번의 스텝을 통해 최솟값으로 다가가는 것을 경사 하강법이라고 합니다
경사는 기울기를 이용해 계산합니다.

경사하강법은 왜 쓰이는가?

인공지능은 기본적으로 예측함수와 실측데이터의 오차를 최소화하는 방식으로 학습한다.
실제 우리가 다루는 데이터의 대부분은 완벽한 선형이나 곡선이 아니므로 실제 값과 차이가 생길
수 있다.
이 오차를 최소화시킬수록 정확한 계측 모델이라고 볼 수 있다.
딥러닝 학습은 기본적으로 이 오차를 나타내는 수식인 손실함수를 최소화하는 것으로 구현된다.

게다가 실제 분석에서 맞딱드리게 되는 함수들은 닫힌 형태가 아니거나 함수의 형태가 복잡해 계산하기 어려운 경우가 많고, 실제 미분계수를 계산하는 과정을 컴퓨터로 구현하는 것에 비해 경사 하강법은 컴퓨터로 비교적 쉽게 구현할 수 있기 때문이다.

이러한 이유들로 함수의 최소값을 구하기 위해 경사하강법을 사용한다.

경사 하강법 - Epoch

Epoch(에포크) 훈련 데이터셋에 포함된 모든 데이터들이 한 번씩 모델을 통과한 횟수로, 모든 학습 데이터셋을 학습하는 횟수를 의미한다.
https://colab.research.google.com/drive/1ulk4T0ZUORsTRLVUNvtx8bX0QZedUaNw?usp=sharing
다음 코드에서 처럼 epoch를 사용할 수 있다.

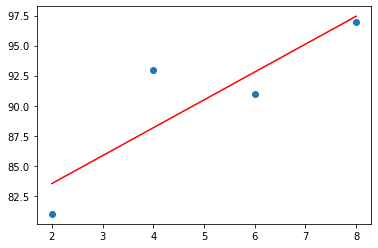
경사 하강법 - Learning Rate

경사하강법의 Learning Rate는 학습률을 뜻한다.
경사하강법에서 학습률(Learning rate)을 값을 지정해야 해야 한다.
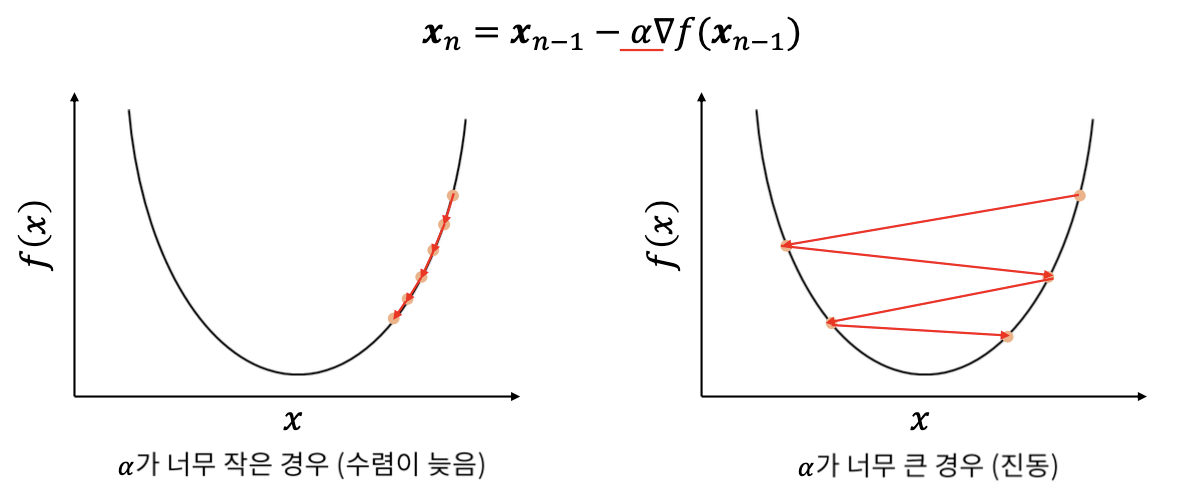
a가 학습률입니다.

학습률이 큰 경우 한 번 이동하는 거리가 커지므로 빠르게 수렴할 수 있다는 장점이 있다. 하지만, 학습률을 너무 크게 설정해버리면 최솟값을 계산하도록 수렴하지 못하고 함숫값이 계속 커지는 방향으로 최적화가 진행될 수도 있습니다.

또, 한편 학습률이 너무 작은 경우 발산하지는 않을 수 있지만 최적의 값을 구하는데 소요되는 시간이 오래 걸린다는 단점이 있습니다. 즉 경사하강법은 적절한 학습률(Learning rate)를 찾는 것이 중요합니다.

글을 마치며

경사하강법에 대해서 간단하게 알아보았다. 수학을 잘하는 편은 아니라서 처음에 와.. 이게 뭐지... 하고 집중하기도 힘들었고 이해하기도 힘들었다. 하지만 이렇게 정리하다보니 어느정도 경사하강법을 이해할 수 있었다.