1절. 군집 모델
군집분석 : 주어진 데이터의 특성을 고려해 데이터의 집단(cluster)을 정의하고 데이터 집단을 대표할 수 있는 대표점을 찾는 것
군집화(clustering) : 데이터의 여러 개의 클러스터로 구분하는 것
1.1. 군집 모델

1) 중심 기반 클러스터링
k개 클러스터의 중심을 찾고 클러스터와의 거리 제곱이 최소화되도록 가장 가까운 클러스터 중심에 개체를 할당한다.
2) 연결 기반 클러스터링
일반적으로 중심보다 군 형성이 잘 됨
계층 클러스터링이라고도 한다.
3) 밀도 기반 클러스터링
일반적으로 중심보다 군 형성이 잘 됨
나머지 데이터셋보다 밀도가 높은 영역으로 정의된다.
(DBSCAN 사용 많이함)
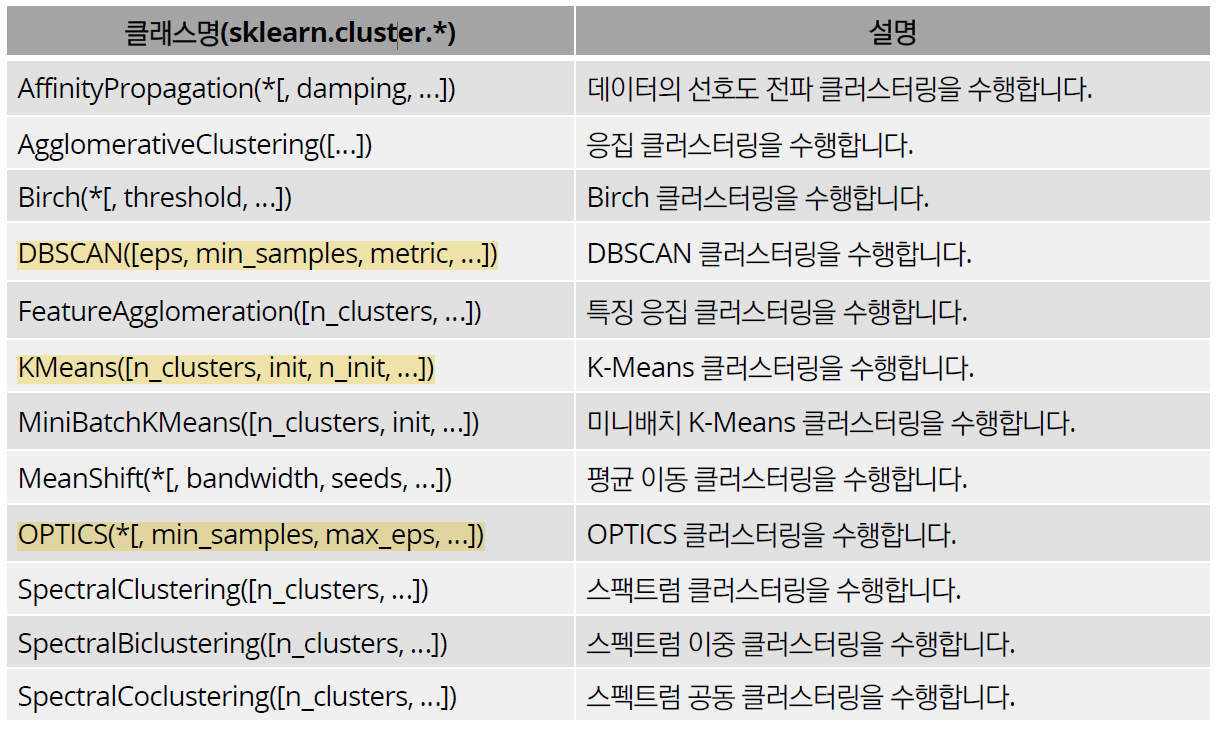
1.2. 싸이킷런의 군집 모델
2절. K-Means 클러스터링
클러스터(cluster) : 독립 변수의 특성이 유사한 데이터의 그룹
클러스터링(clustering) : 주어진 데이터를 여러 개의 클러스터로 구분하는 것
만약 클러스터의 수가 K라면 클러스터링은 모든 데이터에 대해 1~K번 클러스터 중에서 몇
번 클러스터에 속하는지 예측하는 작업
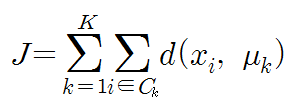
K-Means 클러스터링 : 가장 단순하고 빠른 클러스터링 알고리즘의 하나
목적함수 값이 최소화될 때까지 클러스터의 중심(centroid) 𝜇k와 각 데이터가
소속될 클러스터를 반복해서 찾는 것
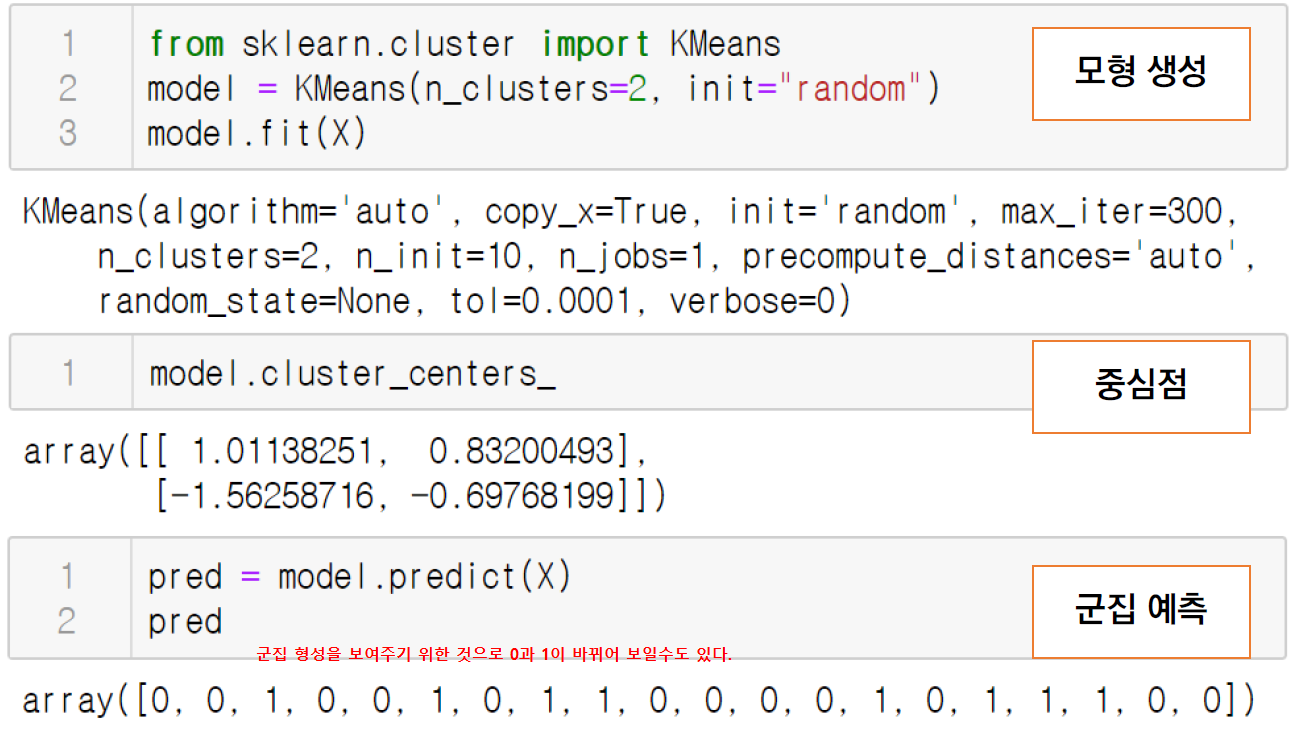
2.1. sklearn.cluster.KMeans
K-Means 클러스터링 알고리즘을 이용해서 모델을 생성하고 학습시킴

K-Means 클러스터링의 세부 알고리즘
- 임의의 중심값 μk를 고릅니다.(보통 데이터 샘플 중의 하나를 선택합니다.)
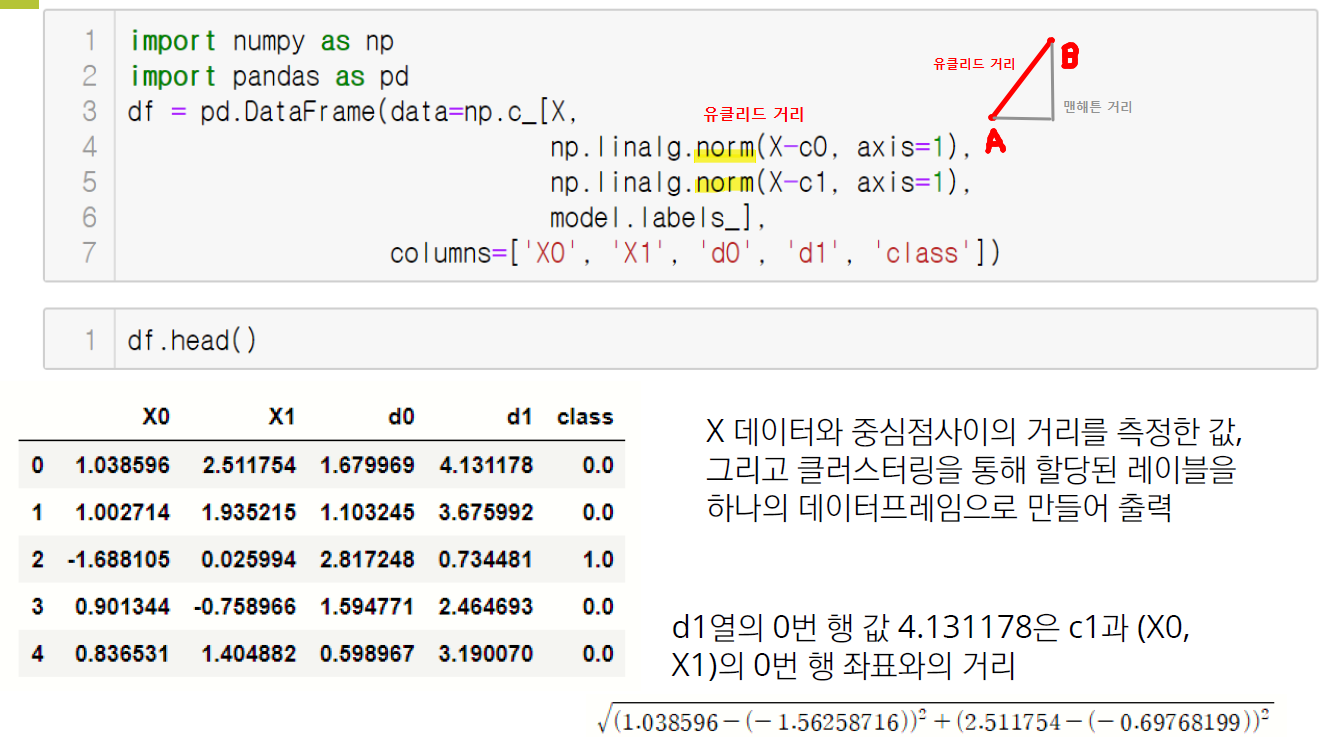
- 중심에서 각 샘플 데이터까지의 거리를 계산합니다.
- 각 데이터 샘플에서 가장 가까운 중심을 선택하여 클러스터 갱신합니다.
- 다시 만들어진 클러스터에 대해 중심을 다시 계산하고 1~4를 반복합니다.
2.2. K-Means 클러스터링
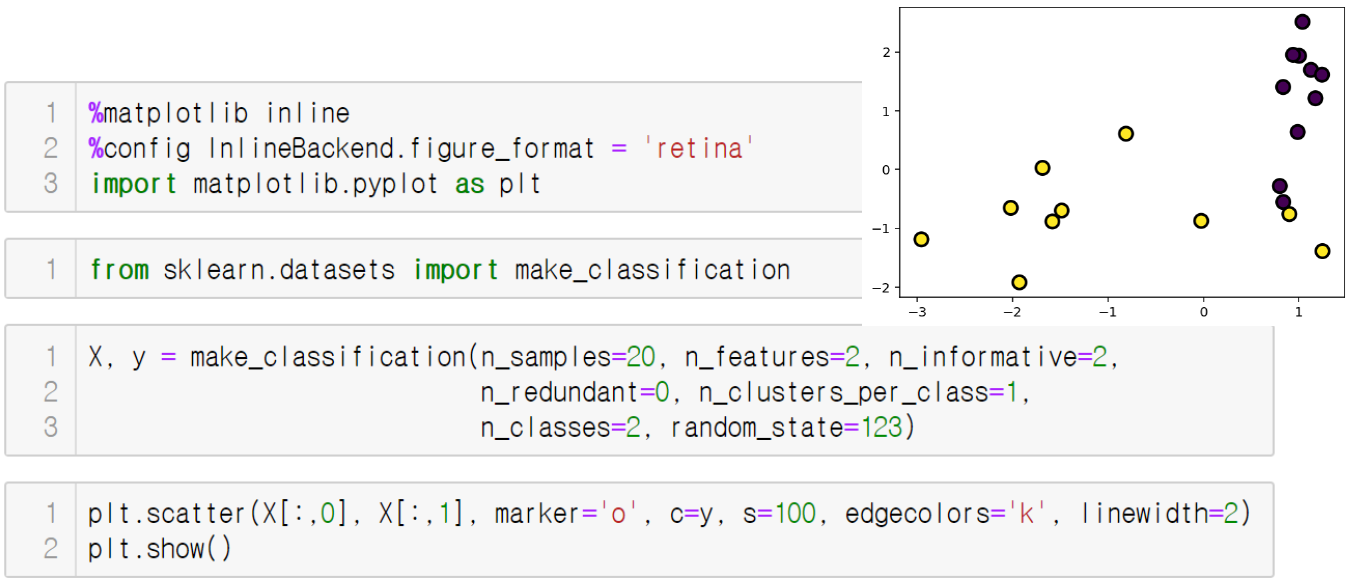
make_classification() 함수는 분류(classification)를 위한 가상 데이터셋을 만드는 함수
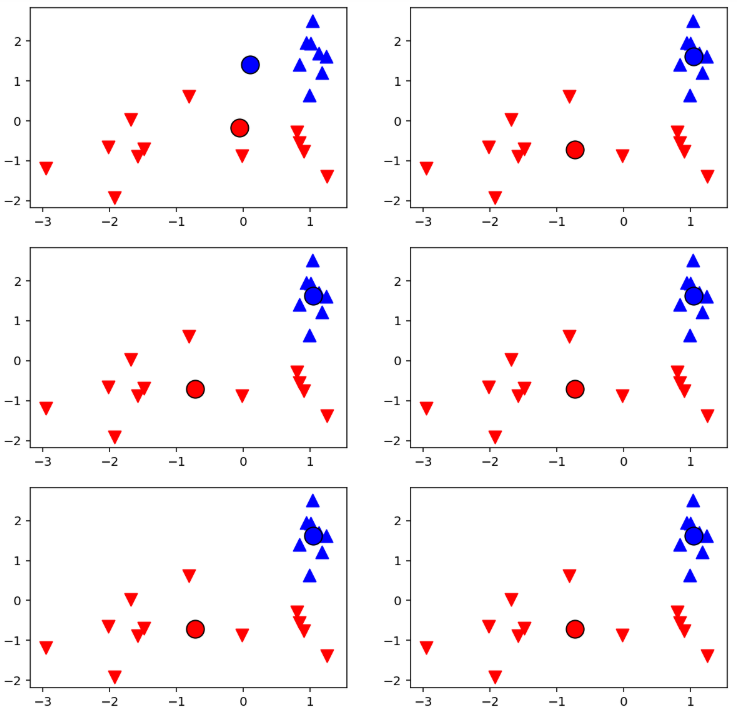
2.3. 회차별 군집 확인하기
KMeans 클래스의 max_iter 인자는 최대 학습 횟수를 지정한다.
이를 통해 학습이 진행되는 과정 동안 중심점을 찾아가는 과정을 시각화할 수 있다.
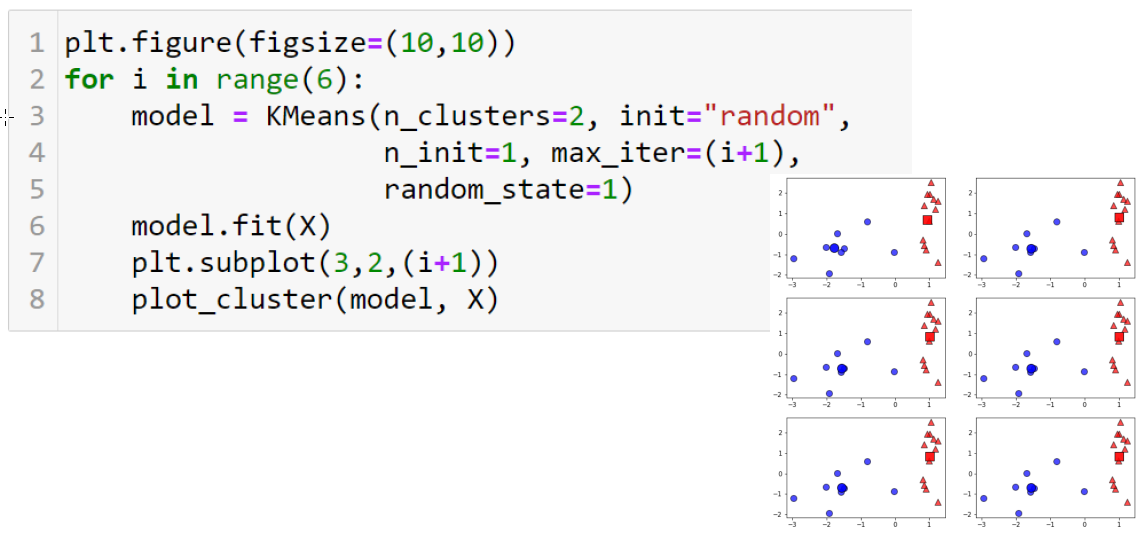
1회부터 6회까지 진행하는 모델을 만든 후 각 모델을 이용해 계산한 중심점과 클러스터링 된 결과를 시각화

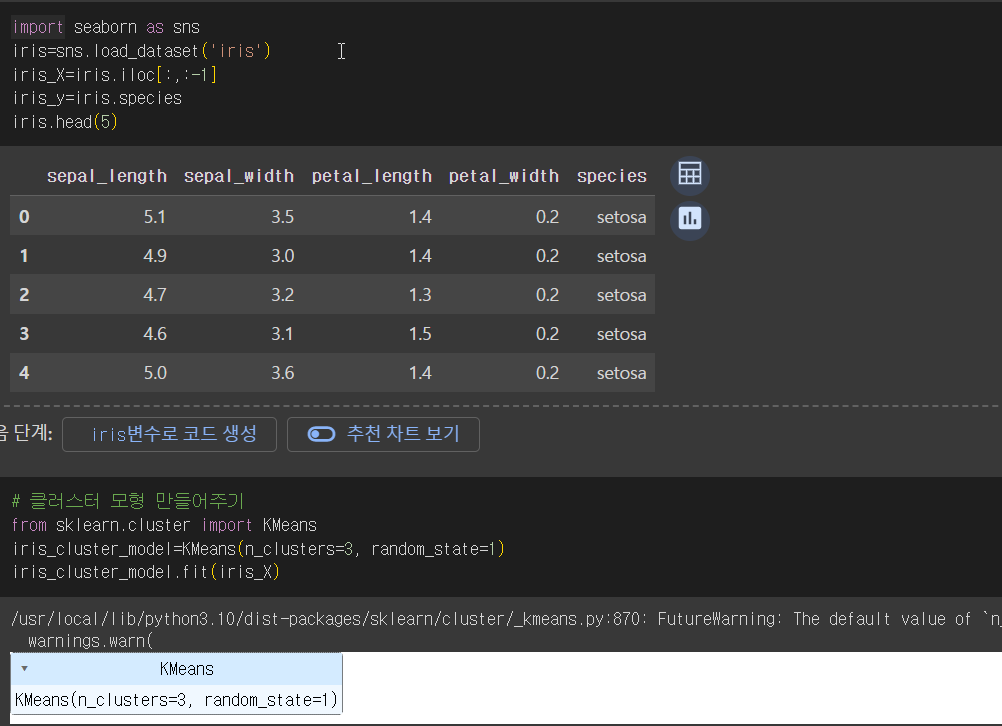
2.4. iris 데이터 군집분석
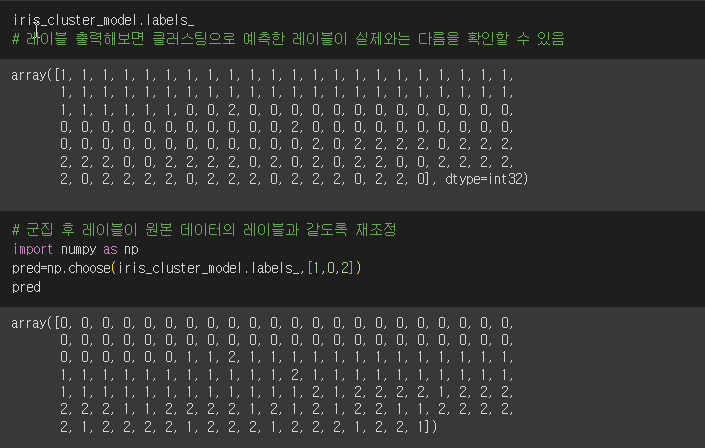
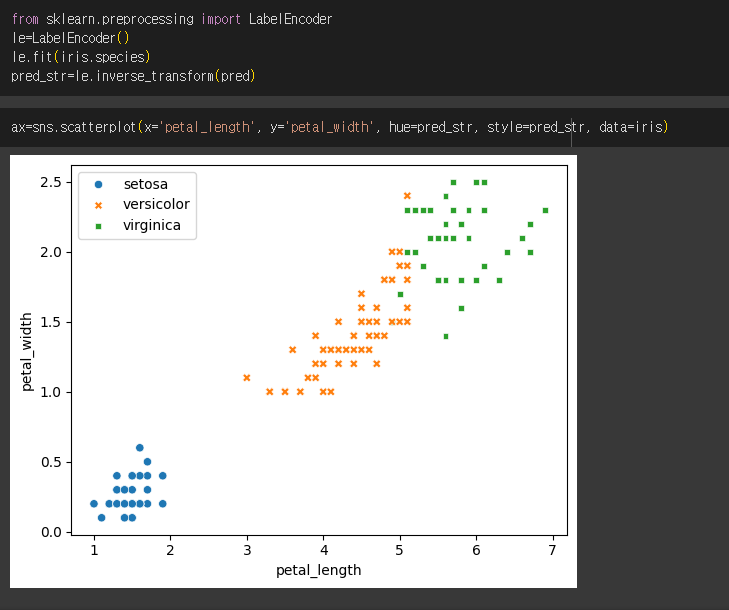
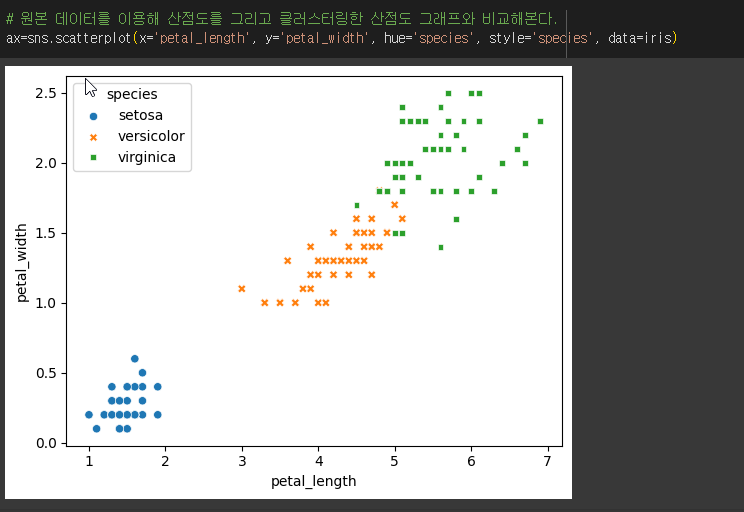
2.5. K-Means 클러스터링의 한계와 극복
k-means 클러스터링은 다음 3가지 경우에 문제가 있다.
- 크기(sizes)
- 밀도(densities)
- 비 구형(non-globular shapes)
1) 크기가 다를 경우
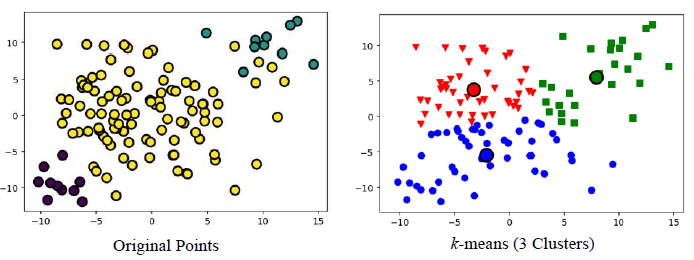
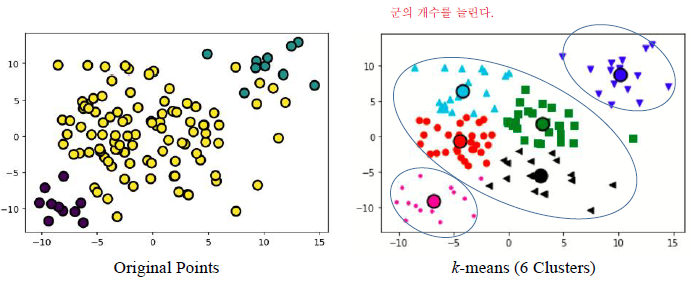
2) 밀도가 다를 경우
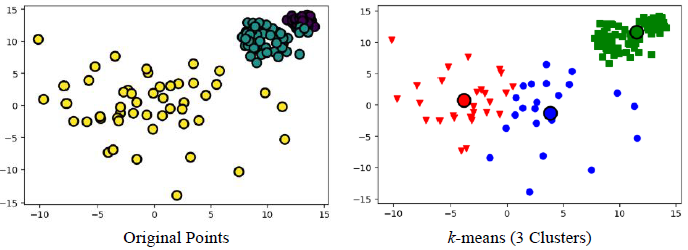
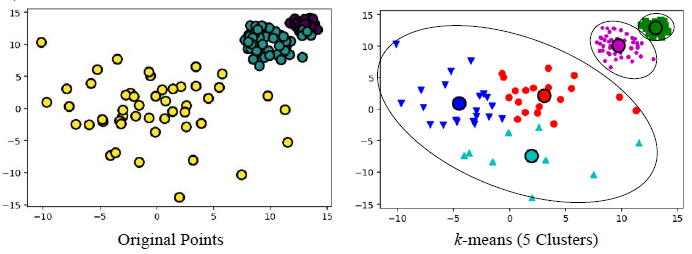
3) 비 구형인 경우
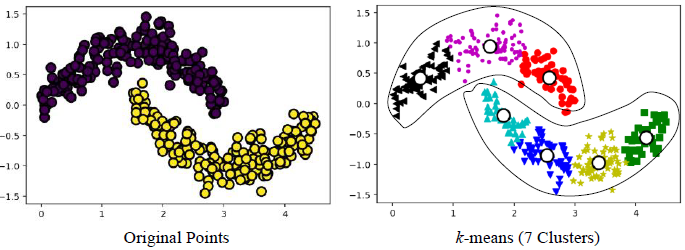
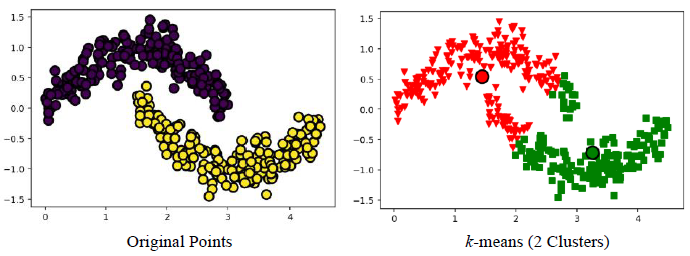
3절. Hierarchical(계층적) 클러스터링
계층적 클러스터링(hierarchical clustering)은 비슷한 군끼리 묶으면서 하나의 군이 될 때까지 군을 묶는 알고리즘이다.
군 사이의 거리를 기반으로 클러스터링을 하는 알고리즘이며, K-Means와는 다르게 군집의 수를 미리 정해주지 않아도 된다.
계층적 군집분석은 덴드로그램(dendrogram()) 함수를 이용하면 손쉽게 시각화할 수 있다.
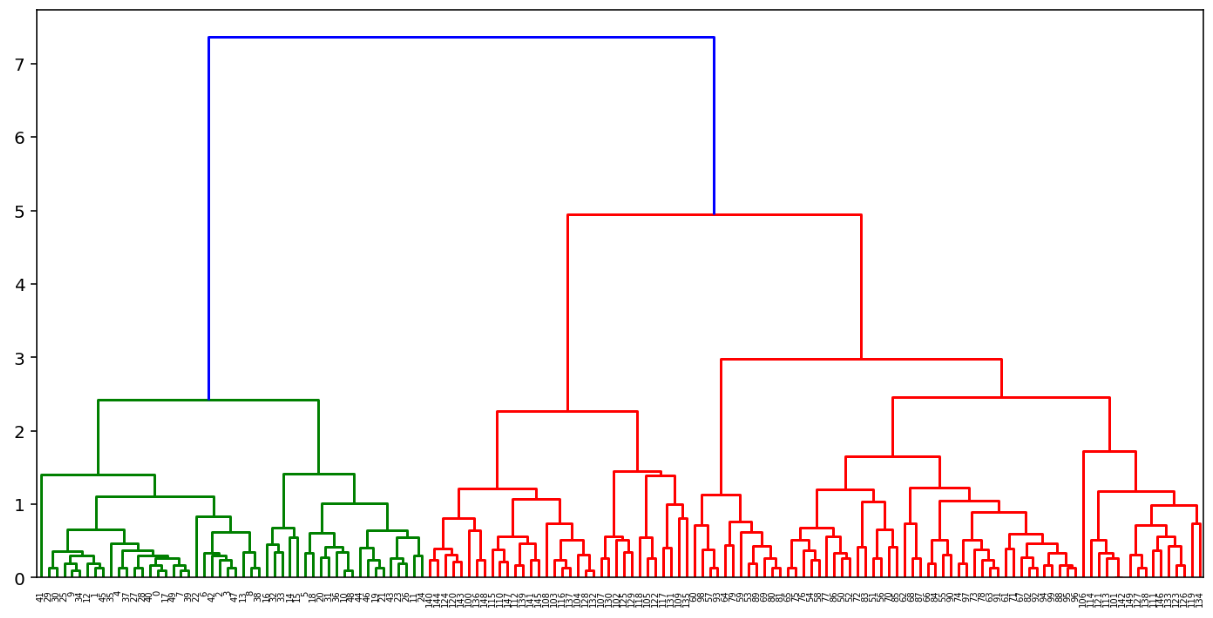
3.1. 계층적 분석 방법

3.2. 계층 분석을 통한 군집의 수 결정
계층적 군집은 최종적으로 1개의 군집으로 모든 데이터를 클러스터링한다.
실제로는 n개의 군집으로 나눠야 함
dendrogram에서 보면 위로 올라갈 수 록 클러스터는 병합
적정한 y값에서 클러스터링을 멈추면 n개의 군까지만 클러스터링이 됨
y=4(수평선이 표시된 곳)에서 클러스터링이 멈추면 총 3개의 클러스터로 군집이 됨
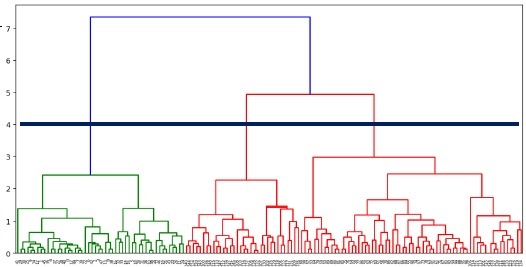
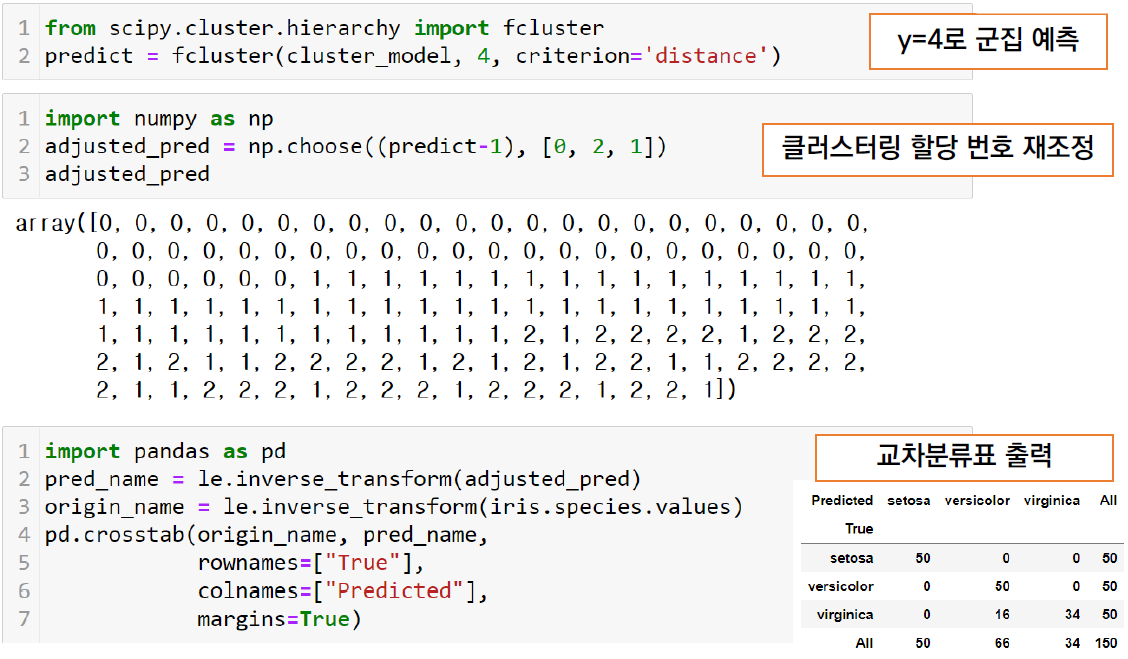
fcluster() 함수를 이용해서 y값을 지정해서 클러스터링을 멈추게 함
y값을 낮게하면 더 많은 클러스터가 만들어진다.

산점도 출력