Array and Hash

DeadWhale·2023년 2월 12일

❕ 책을 읽던 중 배열의 부분을 읽다가 궁금한점을들 정리하기 위해 작성하게 되었다.

어느 정도 개발을 활용하면서 컬렉션들은 주로 만지다 보니 해시 접근 방식을 공부해 알고 있었지만.
배열 인덱스 접근 방식이 어떤식으로 되는지 몰랐던 것같다.
이 부분에 대해 학습해 보았다.

자바의 배열은 메모리의 연속적으로 할당된 공간이다.

int[] arr = new int[5]

이러한 형태로 5칸의 배열을 할당 하게 된다.

배열은 특징은 4가지 정도 있다.

배열의 크기는 생성 시에 정해지며, 변경할 수 없다.
인덱스를 이용하여 배열의 요소에 빠르게 접근할 수 있습니다.
배열은 메모리 상에서 연속된 공간에 할당되므로, 인덱스를 이용한 접근이 빠릅니다.
다차원 배열의 경우, 각 차원마다 크기가 다를 수 있습니다.

배열에서 빠른 인덱스 접근시에는 이러한 느낌으로 접근한다.

배열이 생성되고 배열의 공간이 heap영역에 할당된다.
할당된 메모리중 시작 주소 ( 배열[0]번의 주소 )를 변수에 저장한다
- 위에서는 arr변수에 저장되게 된다.
결과적으로 5칸의 배열 공간은 heap 내부에 선언되고
그중 1번 칸의 주소는 stack에 할당되어 있는 arr변수에 저장된다.
예외적으로 배열이 지연변수로 선언되고 메소드 내에서 생성될 때는 변수와 저장된 메모리 공간이 모두 Stack 영역에 할당된다.

배열 접근 방식과 해시 접근 방식의 차이점

배열의 경우 배열을 선언하는 순간 heap 영역에 모든 공간이 할당된다.

이때 생성된 공간을 추가,삭제 될 수 없다

그렇다면 그려보자면 이런 느낌이 된다.

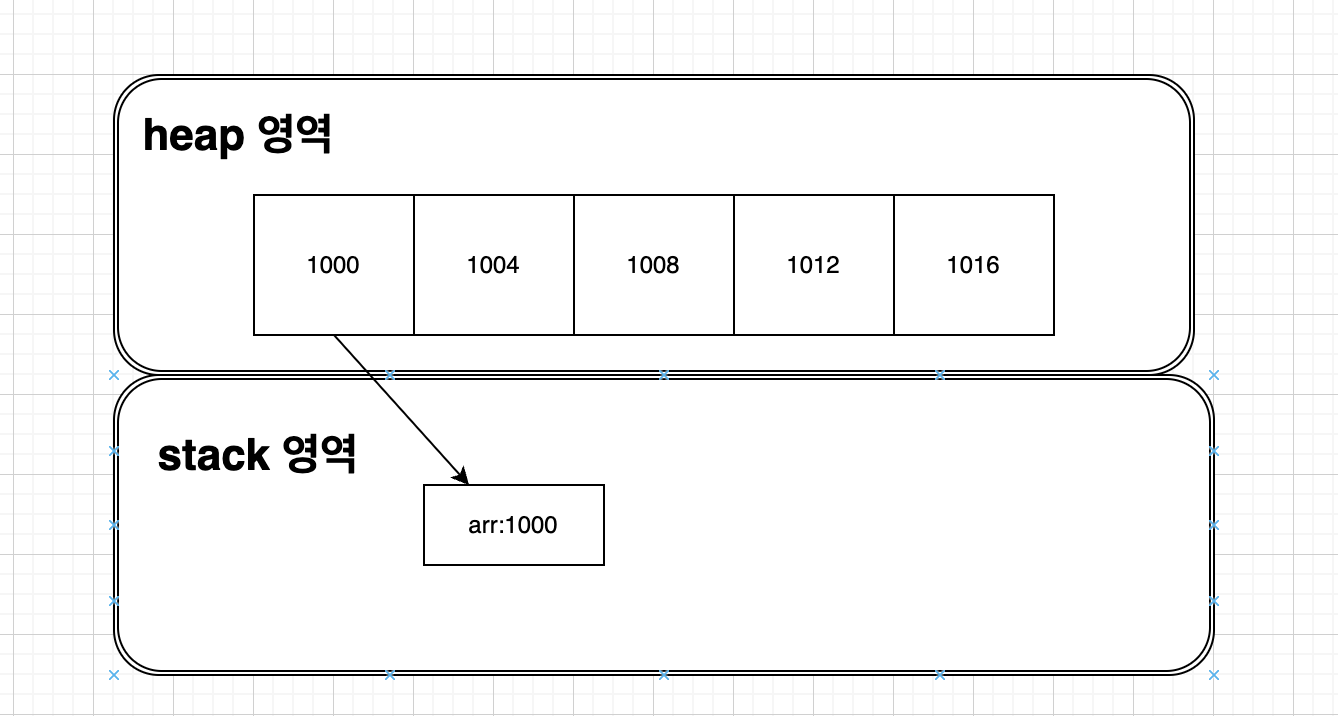
그렇다면 내가 arr[0]에 접근시 나는 stack에 가지고 있는 메모리 주소를 기반으로 연산하여
바로 찾아 갈 수 있게된다.

BaseAddress + ( index * 배열 타입의 길이)

int : 4

long :8

내가 만든 객체 : 객체 프로퍼티 크기의 합

객체 프로퍼티의 크기의 합은 객체안에 선언되어 있는 자료형의 크기와
메소드코드의 길이에 따라 정해진다.
class c{
	int a;
    String b;
    boolean c;
}
int (4 Byte) + String(4 Byte) + boolan (1 Byte) = 9Byte가 프로퍼티 합계 사이즈가 된다.
String은 참조 타입이기 때문에. 기본적으로 4byte 크기의 메모리 주소만 가지고 있는다.

0번을 찾아갈 경우
- 1000 + ( 0 * 4) ⇒ 1000
2번을 찾아갈 경우
- 1000 + ( 2 * 4 ) ⇒ 1008
5번을 찾아갈 경우
- 1000 + ( 5 * 4 )
- 1020의 메모리 위치를 찾아가게 되는데 이때는 배열의 범위를 벗어나니 에러 발생

해시테이블

해시 접근 방식은

키를 가지고 해쉬 함수를 통해 해쉬 코드를 계산한다.
해시값를 모듈러 연산을 통한 다음 나온 값을 인덱스로 사용해 해시 테이블을 찾아간다.
해당 위치로 찾아가면 값을 비교해 동일한 경우 반환한다.
Hash Colision 이 발생하는 경우에는 해결 방식이 여러가지가 있다.
- JAVA의 경우에는 chaining으로 해결하고 있다.
- 테이블에 이미 값이 있는 경우 Linked List를 활용해 확장 저장한다.

❕ 내가 가장 궁금했던 부분은 여기 였다
모듈러 연산 후 해당 인덱스에 값이 있다면 링크드 리스트 구조를 활용해 확장한다 까지는
이해가 잘 되었지만.

만약 진짜~~만약 , 모듈러 연산 후 나온 값이 계속 동일하다면 링크드리스트에 계속 추가 되게되니
링크드리스트의 노드를 탐색하는 시간이 오래 걸리게 된다면
해시테이블의 빠르다는 장점이 없는게 아닌가 였지만

더 알아본 결과 키 충돌은 매우 드물고 해시 테이블 확장을 통해 해결할 수 있다고 한다.
해시테이블 크기 변경시 발생하는 이벤트도 재밌는데 이건 나중에 해시 테이블에 대해 글을 적을때 다시 한번 자세하게 적어봐야 겟다.

❕ 모듈러 연산을 예전에 해쉬를 공부하면서 처음 알게 되었는데.
어려운 연산이 아닌 단순한 나머지 연산을 의미한다.

테이블이 크기가 10일때 , 해시 값이 12 일경우 해시값%테이블 크기(12%10)인 2번 인덱스에 k:v가 저장되게 된다.

결론

항목	해시 접근 방식	배열 인덱스 접근 방식
키의 유형	다양한 유형의 키 사용 가능	정수 타입의 인덱스만 사용 가능
검색 속도	평균적으로 O(1)	O(n)
접근 속도	O(1)~O(n)	O(1)
공간 복잡도	높은 공간 복잡도(배열이 3개 필요)	낮은 공간 복잡도
충돌 해결 방식	체인(chaining)

해시 테이블의 경우 String , int , 객체로도 키로 사용할 수 있다.
배열같은 경우 배열 접근시 인덱스를 이용 계산해야 되서 인덱스값이 정수 형태여야 한다.
배열 인덱스 검색속도가 왜 O(n) 인지 궁금했는데 내가 생각하는건 배열 인덱스 접근이고
배열에서 특정한 값을 찾게 되는 경우 배열의 길이(N) 만큼 전부 탐색하기 때문에 O(n)이 나오는 것이였다.
테이블은 구성하는데 자원이 배열과 비교해 차이가 많이 난다. 배열은 단순히 메모리 공간만 있으면 되지만 해시테이블은 구성하는데 자원이 많이 들어간다.
- 해시 값을 저장하는 배열 : 키값에 대한 해시 값을 저장하는 공간이 필요
- 키 값을 저장하는 배열 : 키 값들을 저장하는 공간이 필요
- 값을 저장하는 배열 : 키 값과 대응되는 값을 저장하는 공간이 필요
- 3개의 배열이 생기면서 해시테이블을 구성하게 된다.
- 키 값이 11개면 테이블의 크기는 11개의 공간이 필요하다.
  
  배열은 항상 O(1)으로 접근하지만 해시는 O(1) ~ O(n) 사이의 속도로 접근할 수 있다.
  
  다만 배열은 한번 생성 된 후 배열의 크기는 불면하지만( 새로운 배열에 복제확장하는 경우 제외)
  해시 테이블은 확장, 축소가 가능해 가변적이라는 차이점이 있다.

❕ 사실 글을 작성하고 나니 배열과 비교할거면 링크드 리스트가 더 적합하지 않았나
생각이 들긴한다. 하지만 왜 작성했나 생각해보니
나는 배열의 인덱스 접근과 해시 테이블이 접근 방식이 비교하고 싶어서 이런 글을 쓰게 되었으니
나중에 컬렉션에 대해 글을 작성할때에는 배열과 리스트의 비교를 다시 해봐야겟다.