
[문제 바로가기] https://www.acmicpc.net/problem/17298
📌문제 설명
크기가 N인 수열 A = A1, A2, ..., AN이 있다. 수열의 각 원소 Ai에 대해서 오큰수 NGE(i)를 구하려고 한다. Ai의 오큰수는 오른쪽에 있으면서 Ai보다 큰 수 중에서 가장 왼쪽에 있는 수를 의미한다. 그러한 수가 없는 경우에 오큰수는 -1이다.
예를 들어, A = [3, 5, 2, 7]인 경우 NGE(1) = 5, NGE(2) = 7, NGE(3) = 7, NGE(4) = -1이다. A = [9, 5, 4, 8]인 경우에는 NGE(1) = -1, NGE(2) = 8, NGE(3) = 8, NGE(4) = -1이다.
입력
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째에 수열 A의 원소 A1, A2, ..., AN (1 ≤ Ai ≤ 1,000,000)이 주어진다.출력
총 N개의 수 NGE(1), NGE(2), ..., NGE(N)을 공백으로 구분해 출력한다.
💡 문제 풀이
이중 반복문으로 코드를 짜면 매우 간단하지만 시간초과가 발생한다. 문제 유형처럼 '스택(stack)'을 사용해야 효율성을 해결할 수 있다.
보통은 스택을 이용했을 때 원소로 담아둔 것이 '(비교를 위한)값'이었는데, 이 문제는 인덱스를 넣는 것이 핵심이다.
풀이 순서는 다음과 같다.
step 1)
변수 선언
- numbers : 주어진 숫자 배열
- res : 오큰수의 결과를 담을 배열 - 찾지못하면 -1이므로 모든 원소를 -1로 초기화했다.
- stack : 스택 - 0번 인덱스부터 오큰수를 찾을 예정이므로 0을 미리 스택에 담았다.
- idx : 주어진 숫자 배열을 탐색하기 위한 인덱스 - 1번 부터 탐색할 예정이므로 1로 초기화했다.
step 2)
스택에 인덱스를 담는 것이 핵심이라고 했다.
여기서 담아야할 인덱스는 '오큰수를 찾지 못한 인덱스'다.
따라서, 오큰수 탐색을 마치는 상황은 다음과 같다.
- 스택이 비어 있을 때 - 오큰수를 모두 찾았으므로 스택은 비워져있다.
- idx가 N이 되었을 때 - 모든 숫자 배열을 탐색했을 때
두 가지 조건을 이용하여 첫 번째 while 문 종료 시점을 설정한다.
step 3)
다음으로 스택에 담겨져 있는 인덱스에 접근하여 오큰수를 찾아줘야 한다.
idx를 통해 주어진 숫자 배열(numbers)을 탐색하고 있기 때문에 idx가 가리키는 숫자와 스택에 담겨져 있는 인덱스가 가리키는 숫자를 비교한다.
주의할 점은 스택의 자료구조 특징인 LIFO 순서대로 진행해야 한다는 것이다.
스택에는 idx위치까지 오큰수를 찾지못한 인덱스들이 순차적으로 담겨져 있기 때문에 아래의 두 값을 비교한다.
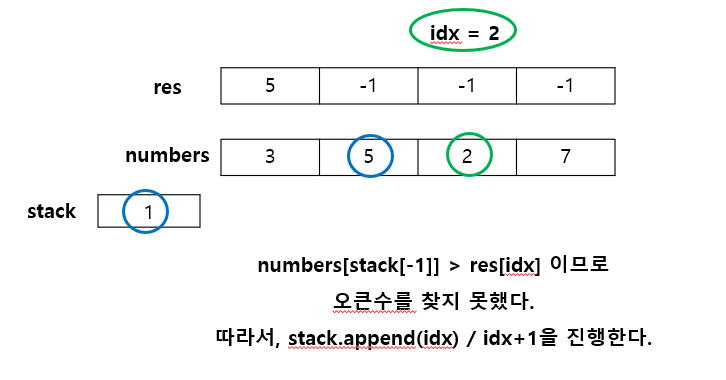
- numbers[stack[-1]] 스택의 마지막 원소에 해당하는 인덱스가 가리키는 값
- numbers[idx]
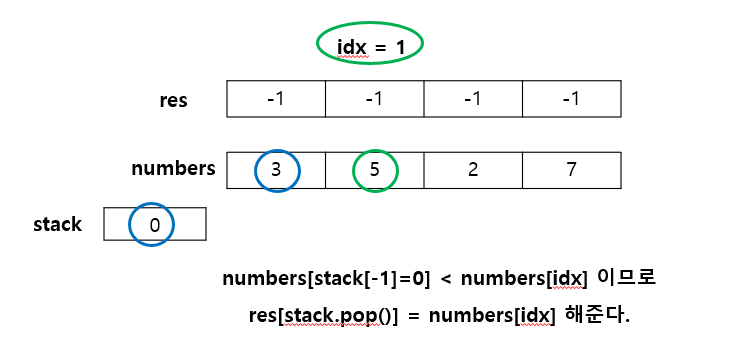
만약, idx가 가리키는 숫자가 스택의 마지막 인덱스가 가리키는 숫자보다 크다면 오큰수를 찾은 것이므로 스택에서 pop하여 res[stack.pop()]에 idx가 가리키는 숫자로 최신화한다.
step 3)은 스택에 원소가 있을 때와 numbers[stack[-1]] < numbers[idx] 일 경우 반복 진행한다.
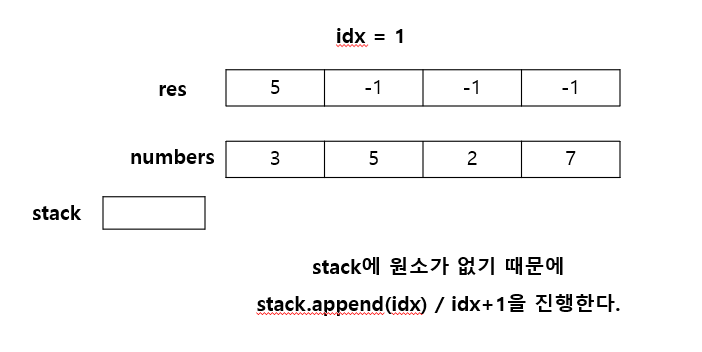
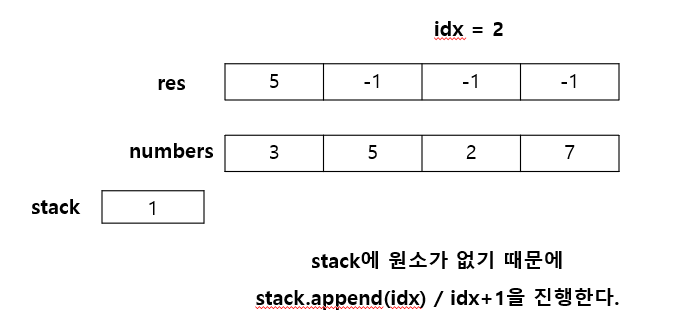
만약, idx에 위치하였을 때 오큰수가 없다면(= 스택에 원소가 없다면) 다음 idx의 오큰수를 찾기 위해 스택에 idx를 추가하고 idx값은 +1 해준다.
문제 풀이를 위해 첫 번째 예제 입력 - numbers = [3, 5, 2, 7]의 경우 진행을 하면 다음과 같다.
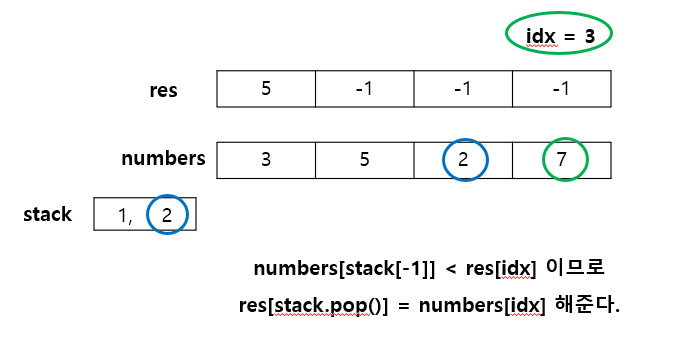
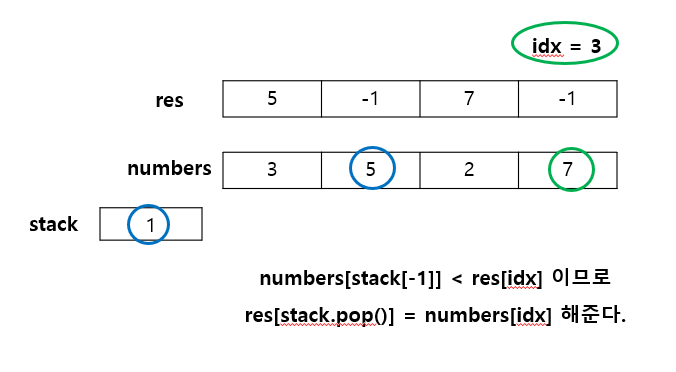
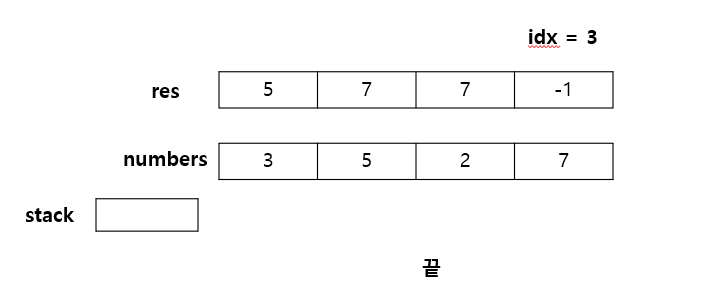
코드는 다음과 같다.
import sys
N = int(sys.stdin.readline())
numbers = list(map(int, sys.stdin.readline().split()))
res = [-1] * N
stack = [0]
idx = 1
while stack and idx < N:
while stack and numbers[stack[-1]] < numbers[idx]:
res[stack.pop()] = numbers[idx]
stack.append(idx)
idx += 1
print(' '.join(map(str, res)))'스택을 이용했을 때 이러한 문제도 풀 수 있구나...' 하고 신기해했던 문제였다.
어떻게 접근할지 이해만 하면 굉장히 쉬운문제지만 생각의 전환이 쉽지 않았다.

