[문제 바로가기] https://www.acmicpc.net/problem/17472
📌문제 설명
섬으로 이루어진 나라가 있고, 모든 섬을 다리로 연결하려고 한다. 이 나라의 지도는 N×M 크기의 이차원 격자로 나타낼 수 있고, 격자의 각 칸은 땅이거나 바다이다.
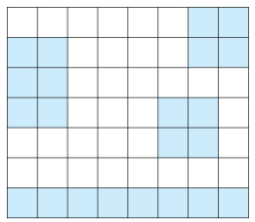
섬은 연결된 땅이 상하좌우로 붙어있는 덩어리를 말하고, 아래 그림은 네 개의 섬으로 이루어진 나라이다. 색칠되어있는 칸은 땅이다.
다리는 바다에만 건설할 수 있고, 다리의 길이는 다리가 격자에서 차지하는 칸의 수이다. 다리를 연결해서 모든 섬을 연결하려고 한다. 섬 A에서 다리를 통해 섬 B로 갈 수 있을 때, 섬 A와 B를 연결되었다고 한다. 다리의 양 끝은 섬과 인접한 바다 위에 있어야 하고, 한 다리의 방향이 중간에 바뀌면 안된다. 또, 다리의 길이는 2 이상이어야 한다.
다리의 방향이 중간에 바뀌면 안되기 때문에, 다리의 방향은 가로 또는 세로가 될 수 밖에 없다. 방향이 가로인 다리는 다리의 양 끝이 가로 방향으로 섬과 인접해야 하고, 방향이 세로인 다리는 다리의 양 끝이 세로 방향으로 섬과 인접해야 한다.
섬 A와 B를 연결하는 다리가 중간에 섬 C와 인접한 바다를 지나가는 경우에 섬 C는 A, B와 연결되어있는 것이 아니다.
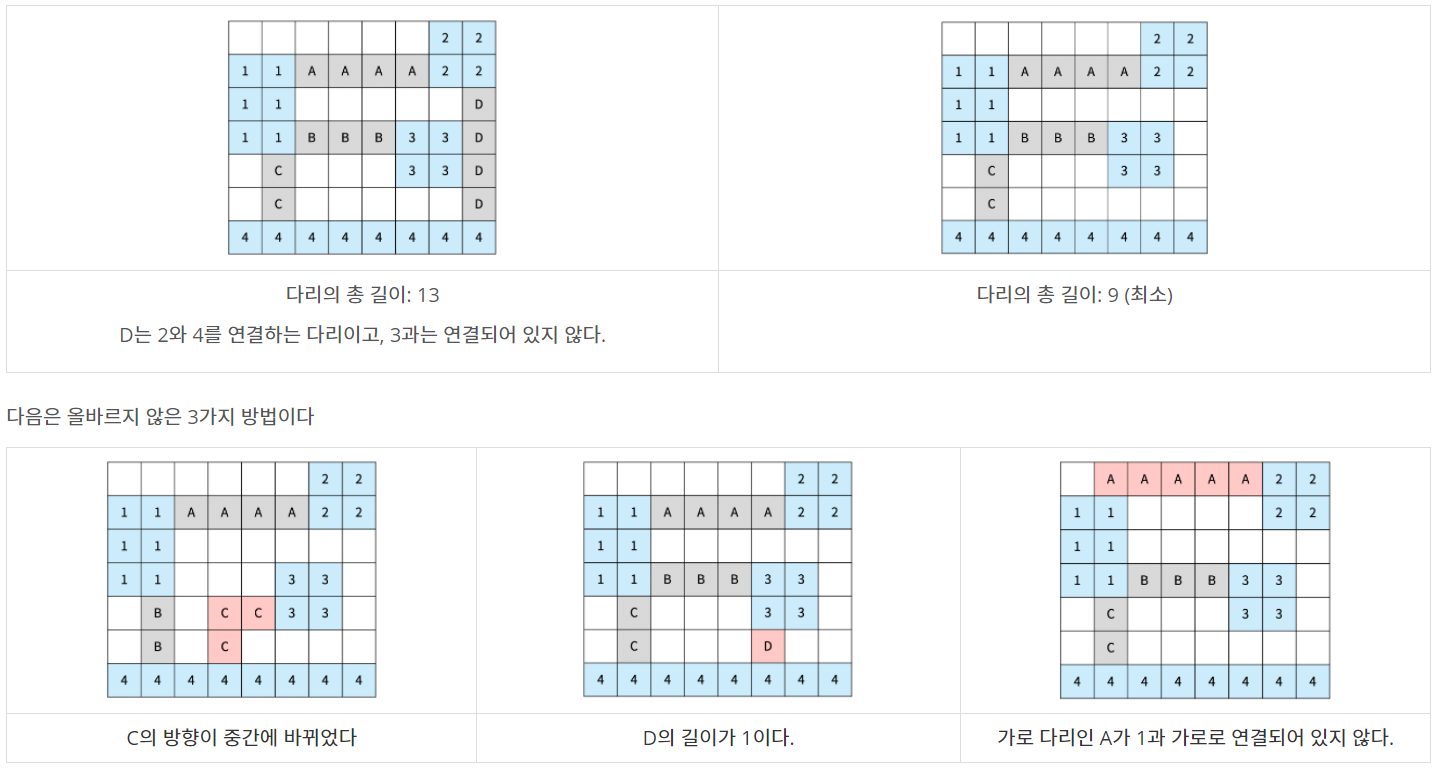
아래 그림은 섬을 모두 연결하는 올바른 2가지 방법이고, 다리는 회색으로 색칠되어 있다. 섬은 정수, 다리는 알파벳 대문자로 구분했다.
다리가 교차하는 경우가 있을 수도 있다. 교차하는 다리의 길이를 계산할 때는 각 칸이 각 다리의 길이에 모두 포함되어야 한다. 아래는 다리가 교차하는 경우와 기타 다른 경우에 대한 2가지 예시이다.
나라의 정보가 주어졌을 때, 모든 섬을 연결하는 다리 길이의 최솟값을 구해보자.
입력
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.출력
모든 섬을 연결하는 다리 길이의 최솟값을 출력한다. 모든 섬을 연결하는 것이 불가능하면 -1을 출력한다.제한
- 1 ≤ N, M ≤ 10
- 3 ≤ N×M ≤ 100
- 2 ≤ 섬의 개수 ≤ 6
💡 문제 풀이
크루스칼(Kruskal) 알고리즘을 활용하여 해결한 문제
step 1)
섬들간의 연결관계를 파악하기 위해서는 섬마다 고유번호가 필요했다.
어떤 섬인지 모르면 누락된 섬이 무엇인지 파악하기 힘들기 때문!
따라서, BFS를 이용하여 탐색하면서 섬마다 고유번호를 부여하였다.
- country : 입력 받는 2차원 배열(나라)
- cnt : 섬에게 부여하는 고유번호
- used : BFS 사용시 탐색한 좌표를 담는 배열
- queue : BFS에 사용할 큐(queue)
step 2)
섬들간 연결할 다리를 놓기 위해서는 조건이 있다.
- 조건 1 : 섬 사이에 2개 이상의 거리가 있어야 한다.
- 조건 2 : 직선만 가능하다
cf) 'ㄱ' 형태, 대각선, 교차로 인한 이동은 X
위의 조건을 만족하는(= 생성 가능한) 다리의 후보를 찾고자 했다.
입력받은 2차원 배열(country)에 대해 행, 열(1차원 배열 단위) 모두 탐색한다. → 직선의 경우만 확인(by 조건 2)
시간 절약을 위해 배열의 합이 0이면(= 즉, 섬의 일부분이 존재하지 않으면) 탐색하지 않는다.
- check 함수 : 생성가능한 다리를 찾기 위한 함수
- start : 다리를 놓기 위한 시작지점(섬) 번호
- cnt : 섬 사이의 거리를 측정하기위한 변수 (by 조건 1)
- flag : 시작지점을 설정했는지 여부를 파악하기 위한 Boolean 값
1차원 배열을 탐색하면서 조건 1을 만족하는 후보를 찾는다.
이 때, 생성 가능하다면 (시작지점, 도착지점, 거리)의 형태로 edge 배열에 담는다.
- edge : 생성 가능한 다리 후보들을 담는 배열
step 3)
모든 섬을 연결할 때 최소 거리를 구하는 것이 목표다.
→ 크루스칼(Kruskal) 알고리즘을 사용!
따라서, edge 배열을 '거리'(2번째 인덱스) 기준으로 오름차순 정렬을 한다.
이후, 순서대로 연결하여 모든 다리가 연결되어있다면 거리의 총합을 담은 answer 변수를 출력한다.
만약 모든 섬이 연결되어 있지 않다면 '-1'을 출력한다.
코드는 다음과 같다.
import sys
from collections import deque
# 생성 가능한 다리 찾기
def check(li):
start, cnt = 0, 0
flag = False
for idx in range(len(li)):
if li[idx] and not flag:
flag = True
start = li[idx]
elif not li[idx] and flag:
cnt += 1
elif li[idx] and flag and start != li[idx]:
if start and cnt >= 2:
if (start, li[idx], cnt) not in edge:
edge.append((start, li[idx], cnt))
cnt = 0
start = li[idx]
elif start == li[idx]:
cnt = 0
N, M = map(int, input().split())
country = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
cnt = 1 # 섬 고유번호
used = [] # BFS 사용시 방문여부 판단
queue = deque([]) # BFS에서 사용하는 큐(queue)
edge = [] # 생성가능한 다리 후보를 담는 배열
# BFS를 이용하여 섬 고유번호 붙이기
direction = [(-1, 0), (1, 0), (0, -1), (0, 1)]
for i in range(N):
for j in range(M):
if country[i][j] and (i, j) not in used:
queue.append((i, j))
used.append((i, j))
while queue:
r, c = queue.popleft()
country[r][c] = cnt
for idx in range(4):
nr = r + direction[idx][0]
nc = c + direction[idx][1]
if 0 <= nr < N and 0 <= nc < M:
if country[nr][nc] and (nr, nc) not in used:
queue.append((nr, nc))
used.append((nr, nc))
cnt += 1
# 행 탐색
for row in country:
if sum(row):
check(row)
# 열 탐색
for col in list(zip(*country)):
if sum(col):
check(col)
# 크루스칼(Kruskal) 알고리즘 부분
edge = sorted(edge, key=lambda x:[x[2]])
parents = [i for i in range(cnt)]
rank = [1 for i in range(cnt)]
# 부모를 찾는 함수
def find(v):
if v != parents[v]:
parents[v] = find(parents[v])
return parents[v]
answer = 0
# 합치는 함수(grouping)
def union(v1,v2,w):
global answer
root1,root2 = find(v1),find(v2)
if root1 != root2:
answer += w
if rank[root1] < rank[root2]:
rank[root2] += rank[root1]
parents[root1] = root2
else:
rank[root1] += rank[root2]
parents[root2] = root1
for e in edge:
union(e[0],e[1],e[2])
if max(rank) != cnt-1:
print(-1)
else:
print(answer)
크루스칼(Kruskal) 알고리즘 구현이 기억나지 않아서 100% 해내지 못한게 아쉬웠다.
크루스칼 알고리즘보다 간단하게 반복문으로 설계한 코드는 '백준 질문'과 '블로그'에 올라온 반례를 모두 통과하였는데 제출에서 '틀렸습니다.'가 나왔다...
많은 시간을 투자해도 해결하지 못해 질문을 올렸는데... 차근차근 알아봐야겠다 😥 (feat. 배운 알고리즘은 복습하자;;)
[반례] https://2jinishappy.tistory.com/65 (감사합니다!)