[Algorithm] Programmers : 다음 큰 숫자 by Python

[문제 바로가기] https://programmers.co.kr/learn/courses/30/lessons/12911

📌문제 설명

자연수 n이 주어졌을 때, n의 다음 큰 숫자는 다음과 같이 정의 합니다.

조건 1. n의 다음 큰 숫자는 n보다 큰 자연수 입니다.
조건 2. n의 다음 큰 숫자와 n은 2진수로 변환했을 때 1의 갯수가 같습니다.
조건 3. n의 다음 큰 숫자는 조건 1, 2를 만족하는 수 중 가장 작은 수 입니다.
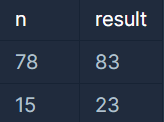
예를 들어서 78(1001110)의 다음 큰 숫자는 83(1010011)입니다.

자연수 n이 매개변수로 주어질 때, n의 다음 큰 숫자를 return 하는 solution 함수를 완성해주세요.

제한 사항
n은 1,000,000 이하의 자연수 입니다.

입출력 예 설명 )
입출력 예#1
문제 예시와 같습니다.

입출력 예#2
15(1111)의 다음 큰 숫자는 23(10111)입니다.

💡 문제 풀이

문제를 풀었지만 너무 지극정성(?)한 하드코딩이다.

다음 큰 수를 찾기위해 이진수에서 나올 수 있는 경우의 수를 따져보았다.
총 3가지의 경우가 존재한다고 생각했다.

1. '1'의 개수와 이진수 길이가 같을 경우
   ex) 15 = 1111(2)
   답은 무조건 +1을 한 값이 된다. 11110(2)

2. 이진수의 마지막 비트가 0이 아닌경우
   ex) 51 = 110011(2)
   '0'이 가장 마지막으로 등장하는 비트 자리와 이후 처음으로 '1'이 등장하는 비트 자리를 바꾼다.(4번째 '0'과 5번째 '1' 자리교환!)
   110011(2) → 110101(2)

3. 이진수의 마지막 비트가 0인 경우
   ex 1) 26 = 11010(2)
   뒤에서부터 이진수를 탐색했을 때 '1'을 경계로 처음으로 '0'이 나타나는 자리에 '1'을 배치한 뒤 해당자리 이후에 모든 '1'을 끝에 배치하면 된다.
   11010(2) → 11100(2)

   ex 2) 78 = 1001110(2)
   1001110(2) → 1010011(2)
   3번째 '0'이 '1'을 경계로 처음으로 '0'이 나타나는 자리이므로 '1'로 배치 그리고 이후 존재하는 2개의 '1'은 끝자리에 배치
   
   

   ※ 만약 12 = 1100(2)처럼 반복문이 끝나도 원하는 '0'의 위치를 찾을 수 없는 경우
   이진수 길이가 1자리 늘어난 상태에서 가장 앞자리를 '1' 그리고 남은 '1'을 모두 뒤에 배치하면 된다.
   1100(2) → 10001(2)

def solution(n):
    binary = bin(n)[2:]
    cnt = binary.count('1')
    if len(binary) == cnt:
        return int('0b' + '10'+'1'*(cnt-1),2)
    else:
        if binary[-1] == '1':
            for i in range(len(binary)-1, 0, -1):
                if binary[i] == '0':
                    return int('0b' + binary[:i] + '10' + binary[i+2:], 2)
        else:
            flag = False
            chk = 0
            for i in range(len(binary)-1, 0, -1):
                if binary[i] == '0':
                    flag = True
                if binary[i] == '1' and flag and chk == 0:
                    chk = 1
                    flag = False
                if binary[i] == '0' and chk == 1:
                    idx = i
                    count_1 = binary[idx+2:].count('1')
                    count_0 = len(binary[idx+2:]) - count_1
                    return int('0b' + binary[:idx] + '10' + '0' * count_0 + '1' * count_1, 2)

            else:
                count_1 = binary.count('1')
                count_0 = binary.count('0')
                return int('0b' + '10' + '0'* (count_0) + '1' * (count_1-1), 2)

다른 사람의 풀이

자연수 n의 '1'의 개수를 변수에 저장(cnt)하고 n+1 부터 1,000,000까지 1씩 증가시키면서 이진수로 변환했을 때 '1'의 개수가 cnt와 같으면 return

def solution(n):
    cnt = bin(n).count('1')
    for i in range(n+1, 1000001):
        if bin(i).count('1') == cnt:
            return i

1,000,000이 제법 큰수라고 생각해서 1씩 증가시키면 시간초과가 날 것 같았는데... 간단하게 풀 수 있었던 문제였다