[문제 바로가기] https://programmers.co.kr/learn/courses/30/lessons/60059
📌문제 설명
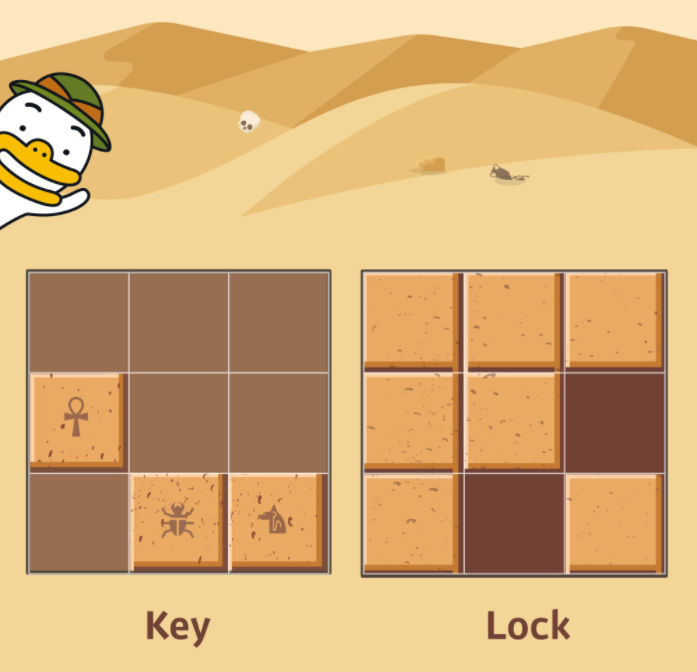
고고학자인 튜브는 고대 유적지에서 보물과 유적이 가득할 것으로 추정되는 비밀의 문을 발견하였습니다. 그런데 문을 열려고 살펴보니 특이한 형태의 자물쇠로 잠겨 있었고 문 앞에는 특이한 형태의 열쇠와 함께 자물쇠를 푸는 방법에 대해 다음과 같이 설명해 주는 종이가 발견되었습니다.
잠겨있는 자물쇠는 격자 한 칸의 크기가 1 x 1인 N x N 크기의 정사각 격자 형태이고 특이한 모양의 열쇠는 M x M 크기인 정사각 격자 형태로 되어 있습니다.
자물쇠에는 홈이 파여 있고 열쇠 또한 홈과 돌기 부분이 있습니다. 열쇠는 회전과 이동이 가능하며 열쇠의 돌기 부분을 자물쇠의 홈 부분에 딱 맞게 채우면 자물쇠가 열리게 되는 구조입니다. 자물쇠 영역을 벗어난 부분에 있는 열쇠의 홈과 돌기는 자물쇠를 여는 데 영향을 주지 않지만, 자물쇠 영역 내에서는 열쇠의 돌기 부분과 자물쇠의 홈 부분이 정확히 일치해야 하며 열쇠의 돌기와 자물쇠의 돌기가 만나서는 안됩니다. 또한 자물쇠의 모든 홈을 채워 비어있는 곳이 없어야 자물쇠를 열 수 있습니다.
열쇠를 나타내는 2차원 배열 key와 자물쇠를 나타내는 2차원 배열 lock이 매개변수로 주어질 때, 열쇠로 자물쇠를 열수 있으면 true를, 열 수 없으면 false를 return 하도록 solution 함수를 완성해주세요.
제한사항
- key는 M x M(3 ≤ M ≤ 20, M은 자연수)크기 2차원 배열입니다.
- lock은 N x N(3 ≤ N ≤ 20, N은 자연수)크기 2차원 배열입니다.
- M은 항상 N 이하입니다.
- key와 lock의 원소는 0 또는 1로 이루어져 있습니다.
- 0은 홈 부분, 1은 돌기 부분을 나타냅니다.
입출력 예
입출력 예에 대한 설명
key를 시계 방향으로 90도 회전하고, 오른쪽으로 한 칸, 아래로 한 칸 이동하면 lock의 홈 부분을 정확히 모두 채울 수 있습니다.
💡 문제 풀이
기본적인 문제해결능력과 2차원 배열을 원하는 자유자재로 변환하여 사용할 수 있는지 묻는 문제
문제에서는 Key를 회전하거나 이동하여 Lock을 푸는 형태이지만 반대로 접근하였다.
왜냐하면 Key는 이동할 경우 사라지는 칸에 대한 고려를 하면서 Lock의 홈 부분(숫자 0)에 일치하는 모양을 찾아야하지만
Lock에서 홈 부분을 포함하는 최소 크기의 사각형을 구하면 Key 2차원 배열에 이동, 회전을 통해서 홈과 돌기가 일치하는 모양이 있는지 찾기만 하면 된다.(배열 밖으로 나가는 이동에 대한 고려가 필요없어진다.)
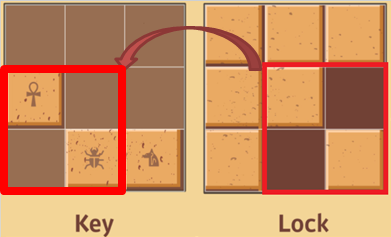
Lock에서 홈 부분을 포함하는 최소 크기의 사각형은 우측 빨간색 사각형이다.
우측의 사각형을 회전, 이동하여 Key와 일치하는 모형을 찾으면(좌측 빨간색 사각형) True를 return하고 그렇지 않으면 False를 return한다.
step 1)
먼저 Lock에서 홈 부분을 포함하는 최소 크기의 사각형을 구하고자 했다.
사각형을 구하기 위해서는 꼭짓점 4개의 좌표(인덱스)를 알아야 한다.
- sr(start row) : 홈 부분이 처음 나온 행 좌표
- sc(start col) : 홈 부분이 처음 나온 열 좌표
- er(end row) : 홈 부분이 마지막으로 나온 행 좌표
- ec(end col) : 홈 부분이 마지막으로 나온 열 좌표
Lock 배열을 탐색하면서 위 4개의 값을 얻는다.
이 때, Lock에서 홈이 없는(=열쇠가 필요없는 경우) 2차원 배열이 주어질수도 있으므로
다음과 같은 조건문을 생성하였다.
if not er + ec: return False즉, 홈 부분이 마지막으로 나온 행, 열 인덱스를 모두 더해도 0인경우는 숫자 0이 없다는 뜻이므로 False를 바로 return 하였다.
step 2)
Lock 으로부터 원하는 2차원 배열을 추출했다.(sr, sc, er, ec 이용)
- want : 홈 부분을 가지는 최소 크기의 사각형(2차원 배열)
- rotate : want를 90도로 회전한 2차원 배열
이후 원본 포함 4번의 회전을 진행하면서 want 배열이 Key 배열을 이동하면서 홈과 돌기가 일치하는 모양이 있는지 파악한다.
step 3)
'이동'에 관한 코딩은 함수를 이용하여 분리시켰다.
- move 함수 : want를 key에 이동시키면서 일치하는 모양이 있는지 찾는 함수
먼저 이동이 가능한 범위를 구한다.
행 : len(key) - len(want)
열 : len(key) - len(want[0])
그리고 이중 반복문을 이용하여 탐색한다.
이 때, 홈과 돌기 부분이 같은 인덱스에서 일치하는지 파악하기 위해서는 want의 복사본과 key의 일부분을 복사한 2차원 배열이 필요하다.
- temp : want를 복사한 배열
- compare : 홈, 돌기 부분이 일치하는지 파악하기 위해 key에서 추출한 배열
- flag : temp와 compare 일치여부를 Boolean으로 표시
temp와 compare은 같은 크기(형태)의 배열이므로 각 위치(행, 열)에서 더한 값이 모두 1이면 True를 return하고 그렇지 않으면 flag를 False 상태로 유지한다.
코드는 아래와 같다.
def move(want, key):
row = len(key) - len(want)
col = len(key) - len(want[0])
for i in range(row+1):
for j in range(col+1):
flag = True
temp = want[::]
compare = [key[r][j:len(want[0])+j] for r in range(i, len(want)+i)]
for x in range(len(temp)):
for y in range(len(temp[0])):
if temp[x][y] + compare[x][y] != 1:
flag = False
break
if flag:
return True
else:
return False
def solution(key, lock):
sr = sc = len(lock)-1
er = ec = 0
for i in range(len(lock)):
if lock[i].count(0):
sr = min(sr, i)
er = max(er, i)
for j in range(len(lock)):
if not lock[i][j]:
sc = min(sc, j)
ec = max(ec, j)
if not er + ec:
return False
want = [lock[r][sc:ec + 1] for r in range(sr, er + 1)]
rotate = want[::]
for i in range(4):
if move(rotate, key):
return True
else:
rotate = []
for j in range(len(want[0])):
rotate.append([want[i][j] for i in range(-1, -len(want) - 1, -1)])
want = rotate[::]
else:
return False다른 사람의 풀이를 보면서 새롭게 배운 내용이 있다. 바로 90도 회전이다.
대각선 대칭은 zip(*iterable) 을 활용한 기억이났지만
90도 회전은 어떻게해야할지 막막해서 반복문으로 해결하였다.
하지만, 90도 회전 역시 zip함수를 이용해서 간단하게 작성할 수 있다.
list(zip(*want[::-1]))또한, 코드를 리뷰하면서 불필요한 변수 선언을 발견하였다.
어짜피, 원본 배열을 회전하는 것인데 굳이 복사를 왜했는지... 모르겠다...
이런 저런 불필요한 코드를 개선했을 때 최종 코드는 아래와 같다.
def move(want, key):
row = len(key) - len(want)
col = len(key) - len(want[0])
for i in range(row+1):
for j in range(col+1):
flag = True
temp = want[::]
compare = [key[r][j:len(want[0])+j] for r in range(i, len(want)+i)]
for x in range(len(temp)):
for y in range(len(temp[0])):
if temp[x][y] + compare[x][y] != 1:
flag = False
break
if flag:
return True
else:
return False
def solution(key, lock):
sr = sc = len(lock)-1
er = ec = 0
for i in range(len(lock)):
if lock[i].count(0):
sr = min(sr, i)
er = max(er, i)
for j in range(len(lock)):
if not lock[i][j]:
sc = min(sc, j)
ec = max(ec, j)
if not er + ec:
return True
want = [lock[r][sc:ec + 1] for r in range(sr, er + 1)]
for i in range(4):
if move(want, key):
return True
else:
want = list(zip(*want[::-1]))
else:
return False문제를 풀고 난 후...
2차원 배열문제를 풀면서 가장 힘들어하는 부분이 좌표(인덱스)다.
아무래도 항상 봐왔던 것이 x, y좌표를 가진 평면이다 보니 아직도 헷갈린다..
또한 문제를 풀면 굉장히 간단한 코드가 존재할 것만 같아서 고민하는데 많은 시간을 쏟지만 실제로 그렇지 않은 경우가 많다...
실제로 나의 코드만하더라도 다른 사람의 풀이보다 평균적으로 짧았다.
보다 많은 문제를 풀어보면서 시간분배와 문제해결에 대한 빠른 판단력을 키워야겠다 😀