[문제 바로가기] https://programmers.co.kr/learn/courses/30/lessons/42890
📌문제 설명
프렌즈대학교 컴퓨터공학과 조교인 제이지는 네오 학과장님의 지시로, 학생들의 인적사항을 정리하는 업무를 담당하게 되었다.
그의 학부 시절 프로그래밍 경험을 되살려, 모든 인적사항을 데이터베이스에 넣기로 하였고, 이를 위해 정리를 하던 중에 후보키(Candidate Key)에 대한 고민이 필요하게 되었다.
후보키에 대한 내용이 잘 기억나지 않던 제이지는, 정확한 내용을 파악하기 위해 데이터베이스 관련 서적을 확인하여 아래와 같은 내용을 확인하였다.
관계 데이터베이스에서 릴레이션(Relation)의 튜플(Tuple)을 유일하게 식별할 수 있는 속성(Attribute) 또는 속성의 집합 중, 다음 두 성질을 만족하는 것을 후보 키(Candidate Key)라고 한다.
유일성(uniqueness) : 릴레이션에 있는 모든 튜플에 대해 유일하게 식별되어야 한다.
최소성(minimality) : 유일성을 가진 키를 구성하는 속성(Attribute) 중 하나라도 제외하는 경우 유일성이 깨지는 것을 의미한다. 즉, 릴레이션의 모든 튜플을 유일하게 식별하는 데 꼭 필요한 속성들로만 구성되어야 한다.
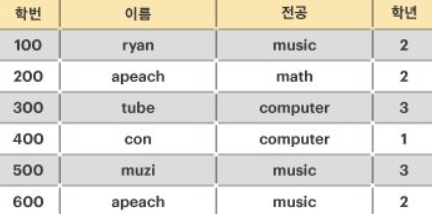
제이지를 위해, 아래와 같은 학생들의 인적사항이 주어졌을 때, 후보 키의 최대 개수를 구하라.
위의 예를 설명하면, 학생의 인적사항 릴레이션에서 모든 학생은 각자 유일한 학번을 가지고 있다. 따라서 학번은 릴레이션의 후보 키가 될 수 있다.
그다음 이름에 대해서는 같은 이름(apeach)을 사용하는 학생이 있기 때문에, 이름은 후보 키가 될 수 없다. 그러나, 만약 [이름, 전공]을 함께 사용한다면 릴레이션의 모든 튜플을 유일하게 식별 가능하므로 후보 키가 될 수 있게 된다.
물론 [이름, 전공, 학년]을 함께 사용해도 릴레이션의 모든 튜플을 유일하게 식별할 수 있지만, 최소성을 만족하지 못하기 때문에 후보 키가 될 수 없다.
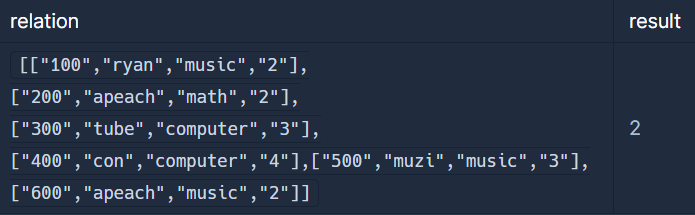
따라서, 위의 학생 인적사항의 후보키는 학번, [이름, 전공] 두 개가 된다.릴레이션을 나타내는 문자열 배열 relation이 매개변수로 주어질 때, 이 릴레이션에서 후보 키의 개수를 return 하도록 solution 함수를 완성하라.
제한사항 )
relation은 2차원 문자열 배열이다.
relation의 컬럼(column)의 길이는 1 이상 8 이하이며, 각각의 컬럼은 릴레이션의 속성을 나타낸다.
relation의 로우(row)의 길이는 1 이상 20 이하이며, 각각의 로우는 릴레이션의 튜플을 나타낸다.
relation의 모든 문자열의 길이는 1 이상 8 이하이며, 알파벳 소문자와 숫자로만 이루어져 있다.
relation의 모든 튜플은 유일하게 식별 가능하다.(즉, 중복되는 튜플은 없다.)입출력 예 )
💡 문제 풀이
쉽게 풀지 못했던 문제(시간이 오래걸렸다)...
이번문제를 풀면서 최소성(minimality)과 파이썬의 zip함수에 대해서 확실히 알 수 있었다...😂
step1)
현재 relation의 리스트는 우리가 원하는 '열'이 아닌 '행'으로 이루어져 있기 때문에 zip(*list))을 이용하여 행과 열의 위치를 바꾸었습니다.
- reverse : relation의 행과 열을 바꾼 결과
step2)
먼저 하나의 속성(열)이 후보키가 되는 것을 확인하고자 했습니다.
reverse를 탐색하면서 하나의 속성(열)이 후보키가 되는지 확인여부는 set을 이용하였습니다.
if len(set(col) == len(col) → 중복값을 제외한 길이와 원본길이가 같을 때
위의 조건을 만족하면 후보키가 됩니다.(answer+1)
else:
만약 위의 조건을 만족하지 않으면 2개 이상의 조합으로 되는지 확인하기 위해 candidate리스트에 따로 담았습니다.
- candidate : 단독으로 후보키가 되지 않는 속성(열)을 담는 리스트
step3)
- find함수 : candidate내의 속성(열) 중 후보키가 있는지 찾는 함수
이후 combination을 이용하여 candidate내의 속성(열)들이 후보키가 될 수 있는지 조합 여부를 확인합니다.
이 때 combination의 r범위는 2부터 len(candidate)까지입니다.
조합의 결과로 나온 속성(열)들을 대상으로 step2 처럼 유일성을 만족하는 후보키가 될 수 있는지 파악합니다. - zip(), set(), len()을 이용하여 확인!
step4)
유일성을 만족했다면 이제는 최소성을 만족시켜야 합니다.
이전에 나온 속성(열)들의 조합이 이후에 추가되어 나타날 수 있으므로
최소성 조건을 위해 keys 리스트를 생성했습니다.
- keys : 유일성과 최소성 모두 만족하는 후보키를 담는 리스트
최소성을 만족시키기 위해서는 유일성을 만족시키는 조합(li)이 keys에 담겨 있는 원소들을 부분집합으로 가지면 안됩니다.
따라서, issubset 함수를 이용하여 부분집합 여부를 확인!
if 유일성을 만족시켰지만 최소성을 만족시키지 못하면 break
else: 유일성과 최소성을 모두 만족시켰다면 keys에 set(li)를 담았습니다.
반복문을 마쳤다면 len(keys) 값을 return
풀이1) 11번 테스트 실패...
from itertools import combinations
def find(candidate):
keys = []
for k in range(2, len(candidate)+1):
for li in combinations(candidate, k):
res = list(zip(*(i for i in li)))
if len(set(res)) != len(res):
continue
for key in keys:
if set(key).issubset(li):
break
else:
keys.append(set(li))
return len(keys)
def solution(relation):
answer = 0
reverse = list(zip(*relation))
candidate = []
for col in reverse:
if len(set(col)) == len(col):
answer += 1
else:
candidate.append(col)
answer += find(candidate)
return answer풀이1로 제출하였는데 11번 테스트가 실패...
아무리 생각해봐도 잘못된 부분이 없다고 생각했는데 질문하기에서 올라온 예제들을 찬찬히 살펴보면서 반례를 찾았습니다.
반례는 다음과 같습니다.
| 1 | 2 | 3 |
| a | b | a |
| c | d | c |
| a | f | a |
| b | f | b |
※첫 행은 속성(열) 번호입니다!!!
위와 같은 relation이 주어진다고 하였을 때
단일 속성으로 후보키가 될 수 있는 것은 없습니다. (유일성 만족X)
하지만 (1, 2), (2, 3)의 조합은 후보키가 될 수 있습니다.
그러나, 풀이1 처럼 단순히 조합의 결과를 통해서 최소성을 판단한다면?
(1, 2)와 (2, 3)은 같은 값이라 판단하게 됩니다.
따라서, 유일성에는 문제가 되지 않으나 최소성을 판단할 때는 조합의 결과가 아니라 인덱스를 이용해서 판단해야 했습니다😂
풀이2) 성공
- idx : candidate의 인덱스 번호를 담은 리스트
풀이1과 다른점은 리스트를 사용했다는 것 말고는 없습니다!
from itertools import combinations
def find(candidate):
keys = []
idx = [i for i in range(len(candidate))]
for k in range(2, len(candidate)+1):
for li in combinations(idx, k):
res = list(zip(*(candidate[i] for i in li)))
if len(set(res)) != len(res):
continue
for key in keys:
if set(key).issubset(li):
break
else:
keys.append(set(li))
return len(keys)
def solution(relation):
answer = 0
reverse = list(zip(*relation))
candidate = []
for col in reverse:
if len(set(col)) == len(col):
answer += 1
else:
candidate.append(col)
answer += find(candidate)
return answer우여곡절 끝에 통과..!!😉