17070번 파이프 옮기기 1

https://www.acmicpc.net/problem/17070

---

아이디어

DP는 아이디어 생각하는 게 어려운 것 같다. 하지만 점화식과 초기값만 잘 생각하면 잘 풀린다.

점화식

graph[i][j][0]: 벽 유무
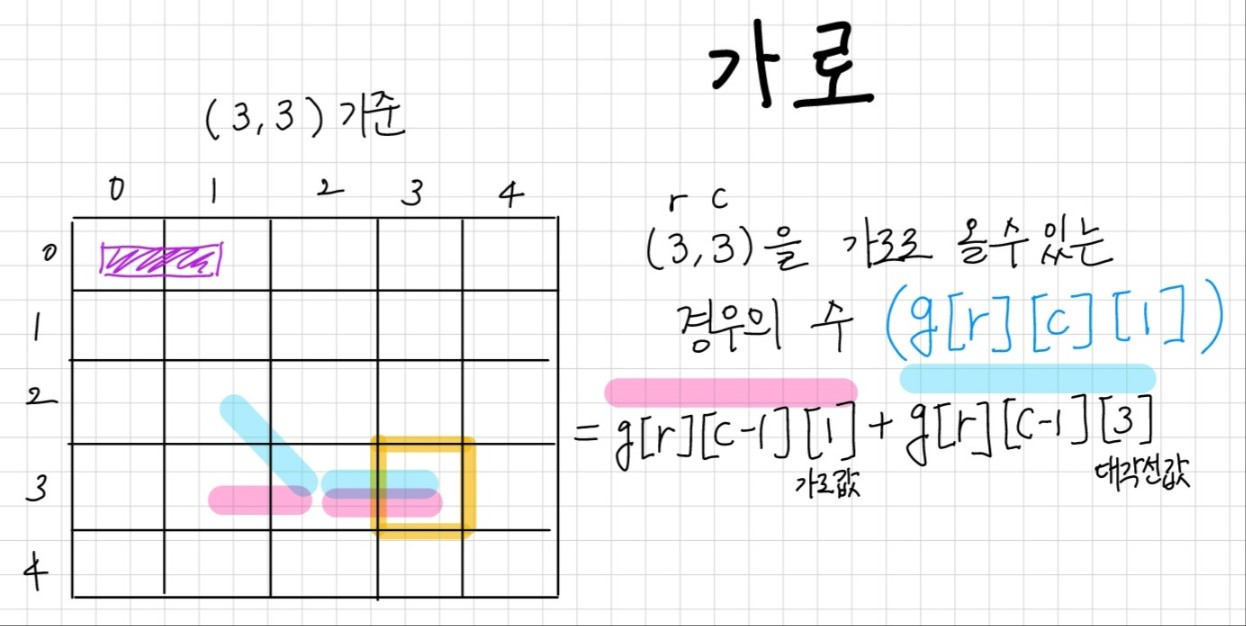
graph[i][j][1]: 끝 방향을 가로 방향으로 파이프를 놓을 수 있는 경우의 수
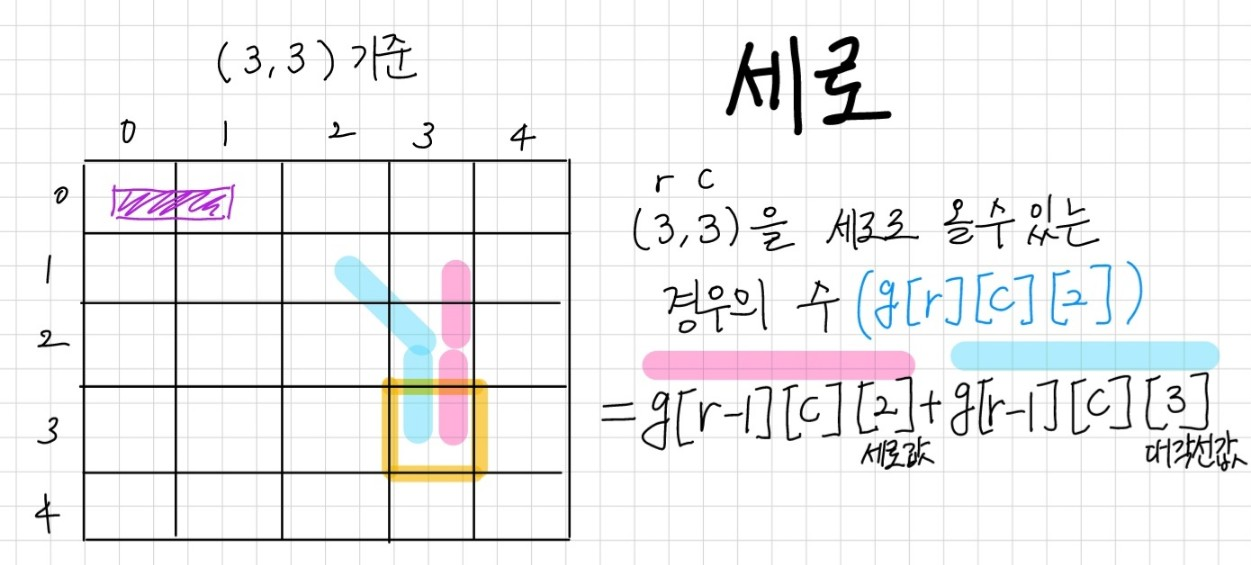
graph[i][j][2]: 끝 방향을 세로 방향으로 파이프를 놓을 수 있는 경우의 수
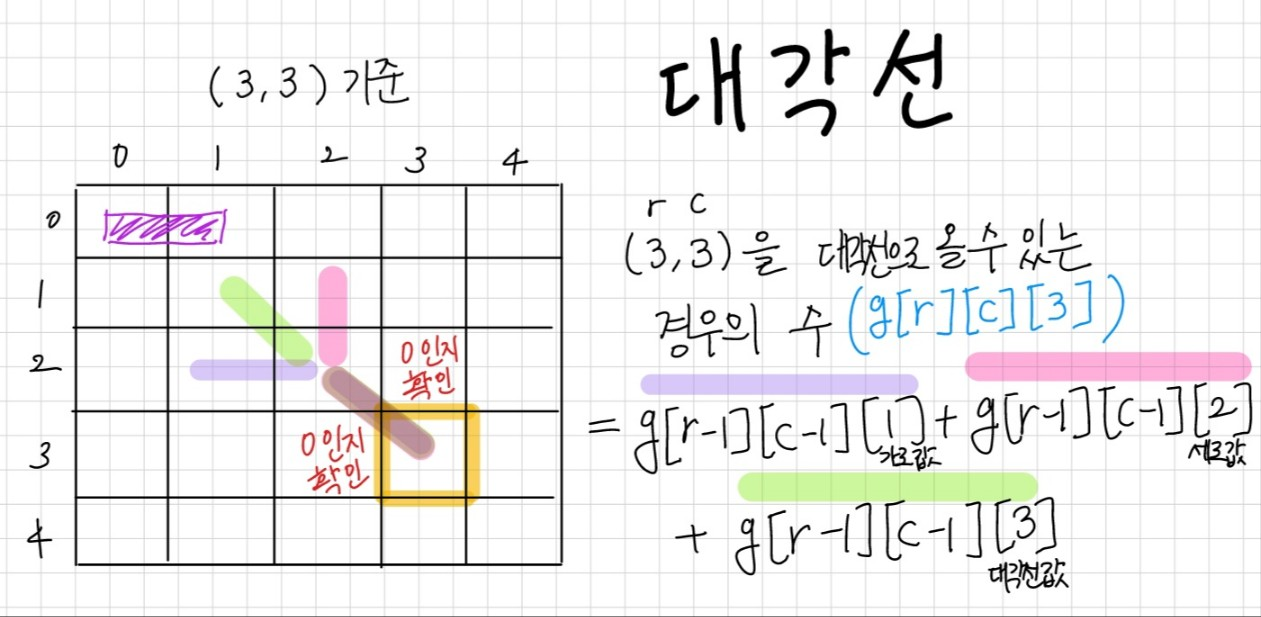
graph[i][j][3]: 끝 방향을 대각선 방향으로 파이프를 놓을 수 있는 경우의 수

그림을 열심히 그려보았다

정리하자면 점화식은 다음과 같다.

graph[r][c][1] = graph[r][c-1][1] + graph[r][c-1][3]
graph[r][c][2] = graph[r-1[c][2] + graph[r-1[c][3]
graph[r][c][3] = graph[r-1][c-1][1] + graph[r-1][c-1][2] + graph[r-1][c-1][3]

초기값

0행과 0열만 생각하면 된다.

0행

우선 0행을 생각해보면 처음 (0,0), (0,1)에 파이프를 놓으므로 벽이 없는 한 계속 가로로 움직일 수 있다.

for i in range(1, n):
    graph[0][i][1] = 1 # 가로값 추가

1부터 한 이유는 끝 방향을 기준으로 하기 때문에 파이프의 시작인 (0,0)에 가로값을 넣을 필요가 전혀 없다.

하지만 가로로 움직이다가 만약 벽을 만나면 그 이후는 0행에서 가로로 못 움직인다. 그래서 조건을 하나 추가해준다.

# 초기값
for i in range(1, n):
    if graph[0][i][0] != 0: break # 벽이 나온 이후에는 가로로 둘 수 X
    graph[0][i][1] = 1 # 가로값 추가

0열

처음 시작을 가로로 하기 때문에 0열은 아예 파이프의 끝이 올 수가 없다.

---

코드

import sys
input = sys.stdin.readline

n = int(input())
graph = [list(map(int, input().split())) for _ in range(n)]
for i in range(n):
    for j in range(n):
        graph[i][j] = [graph[i][j], 0, 0, 0] # [벽유무, 가로, 세로, 대각선]
# 초기값
for i in range(1, n):
    if graph[0][i][0] != 0: break # 벽이 나온 이후에는 가로로 둘 수 X
    graph[0][i][1] = 1 # 가로값 추가

for i in range(1, n):
    for j in range(1, n):
        if i == 0 or j == 0: continue
        if graph[i][j][0] != 0: continue
        # 가로
        graph[i][j][1] = graph[i][j-1][1] + graph[i][j-1][3]
        # 세로
        graph[i][j][2] = graph[i-1][j][2] + graph[i - 1][j][3]
        # 대각선
        if graph[i-1][j][0] == 0 and graph[i][j-1][0] == 0:
            graph[i][j][3] = graph[i-1][j-1][1] + graph[i-1][j-1][2] + graph[i - 1][j - 1][3]

print(sum(graph[n-1][n-1][1:])) # (n,n)의 가로+세로+대각선 경우의 수