Question
개미전사는 부족한 식량을 충당하고자 메뚜기 마을의 식량창고를 몰래 공격하려고 한다. 메뚜기 마을에는 여러 개의 식량창고가 있는데 식량창고는 일직선으로 이어져 있다. 각 식량창고에는 정해진 수의 식량을 저장하고 있ㄷ으며 개미 전사는 식량창고를 선택적으로 약탈하여 식량을 빼앗을 예정이다. 이때 메뚜기 정찰병들은 일직선상에 존재하는 식량창고 중에서 서로 인접한 식량창고가 공격받으면 바로 알아챌 수 있다. 따라서 개미 전사가 정찰병에게 들키지 않고 식량창고를 약탈하기 위해서는 최소한 한 칸 이상 떨어진 식량창고를 약탈해야 한다. 예를 들어 식량창고 4개가 다음과 같이 존재한다고 가정하자.
{1, 3, 1, 5}
이때 개미 전사는 두 번째 식량창고와 네 번째 식량창고를 선택했을 때 최댓값인 총 8개의 식량을 빼앗을 수 있다. 개미 전사는 식량창고가 이렇게 일직선상일 때 최대한 많은 식량을 얻기를 원한다.
개미 전사를 위해 식량창고 N개에 대한 정보가 주어졌을 때 얻을 수 있는 식량의 최댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 식량창고의 개수 N이 주어진다. (3<=N<=100)
둘째 줄에 공백으로 구분되어 각 식량창고에 저장된 식량의 개수 K가 주어진다. (0<=K<=1,000)
출력
첫째 줄에 개미 전사가 얻을 수 있는 식량의 최댓값을 출력하시오.
Solution
a[i]를 i번째 식량 창고까지 얻을 수 있는 식량의 최대값, 즉 i번째 식량 창고까지의 최적의 해로 정의한다. 위의 예시의 경우, dp table은 아래와 같이 구성되어 있다.
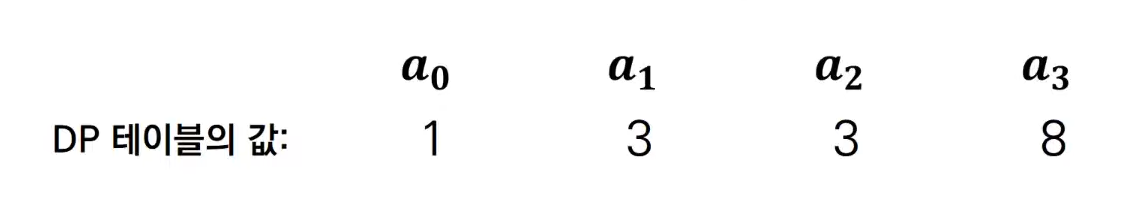
그렇다면 우리는 결국 어떤 위치 i에서 (i-1)번째 창고를 털기로 결정한 경우와 (i-2)번째 창고를 털기로 결정한 경우만을 생각하며 dp 테이블에 값을 넣어가면 된다. 이전의 위치(i-1, i-2, i-3...)에서는 이미 최적의 해를 구한 상태이다.
(i-1)번째 창고를 턴다면 i번째에서 창고를 털 수 없으므로 i번째의 dp table 값은 a[i-1]이 될 것이고,
(i-2)번째 창고를 턴다면 i번째 창고를 털 수 있으므로 i번째의 dp table 값은 a[i-2] + i번째 위치의 식량 갯수가 된다.
Code
n = int(input())
arr = list(map(int,input().split()))
d=[0]*100
d[0]=arr[0]
d[1]=max(arr[0],arr[1])
# 다이나믹 프로그래밍 (Botton-Up)
for i in range(2,n):
d[i]=max(d[i-1],d[i-2]+arr[i])
print(d[n-1])