목차
- 버블 정렬
- 선택 정렬
- 삽입 정렬
1. 버블 정렬
개념 요약
- 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘.
- 인접한 2개의 레코드를 비교하여 큰 경우 오른쪽으로 이동한다.(오름차순)
- 길이가 10이라고 가정할 떄 처음부터 10번 쨰까지 비교, 처음부터 9번째.. 마지막으로 처음부터 2번쨰를 비교한다. (오름차순)
- 오름차순의 경우 접근할 수 있는 가장 오른쪽에 가장 큰 값을 지정한다.
가장 오른쪽 접근 가능한 인덱스가 1씩 감소한다. (n → n - 1, n - 2 ….) - 내림차순의 경우 접근할 수 있는 가장 왼쪽에 가장 큰 값을 지정한다.
가장 왼쪽 접근 가능한 인덱스가 1씩 증가한다. (0 → 1 → 2 …)
구현
void swap(int* array, int left, int right)
{
// 배열의 left index와 right index의 값을 교환하는 함수
int temp = array[right];
array[right] = array[left];
array[left] = temp;
}
void bubbleSort(int* array, int size, bool ascending)
{
// 버블 정렬 구현.
int end = size - 1;
if (ascending == true)
{
while(end)
{
// 가장 큰 값을 오른쪽으로 이동시킨다.
for (int i = 0; i < end; ++i)
{
if (array[i] > array[i + 1])
{
swap(array, i, i + 1);
}
}
--end;
}
}
else
{
while(end)
{
// 가장 작은 값을 왼쪽으로 이동시킨다.
for (int i = end; i > 0; --i)
{
if (array[i - 1] < array[i])
{
swap(array, i - 1, i);
}
}
--end;
}
}
}
- 오름차순의 경우
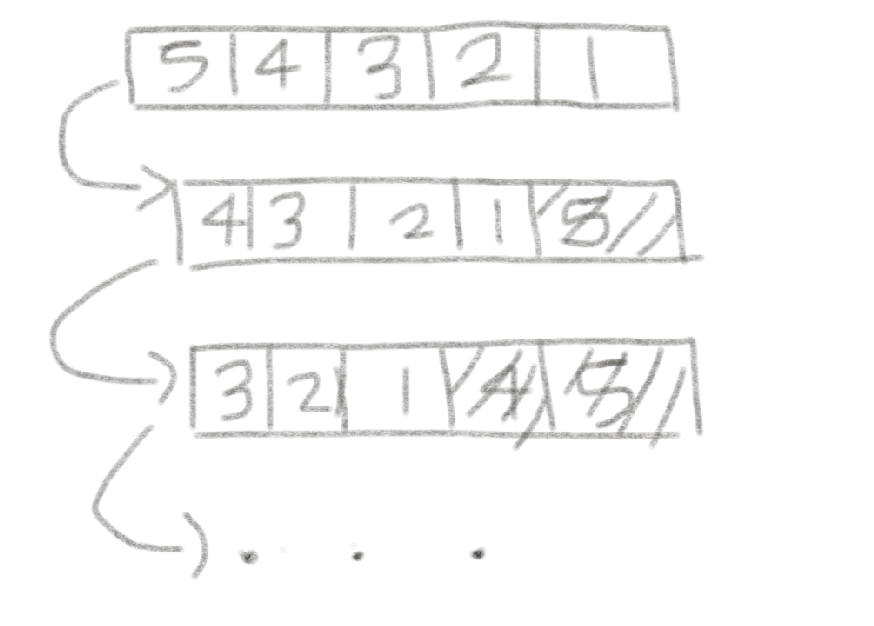
- 내림차순의 경우
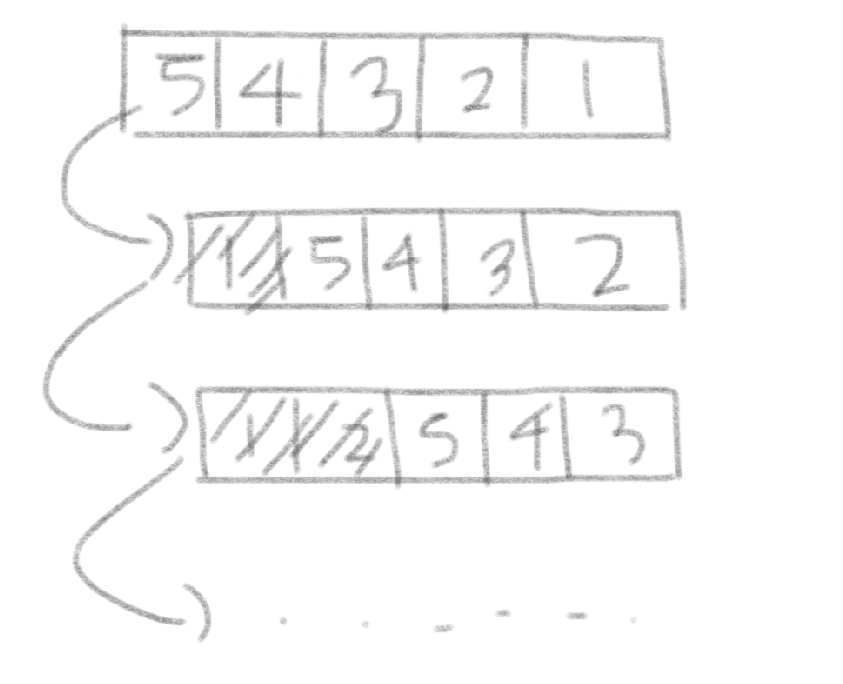
2. 선택 정렬
개념 요약
-
오름차순
- 주어진 리스트 중에 최소 값을 찾는다.
- 그 값을 맨 앞에 위치한 값과 교체한다.
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
-
내림차순
- 주어진 리스트 중에 최대 값을 찾는다.
- 그 값을 맨 앞에 위치한 값과 교체한다.
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
구현
void swap(int* array, int left, int right)
{
int temp = array[right];
array[right] = array[left];
array[left] = temp;
}
void selectionSort(int* array, int size, bool ascending)
{
int end = size - 1;
int start = 0;
if (size < 2)
{
return;
}
if (ascending == true)
{
while(start < end)
{
int swapIndex = -1;
int minValue = array[start];
for (int i = start + 1; i < size; ++i)
{
if (minValue > array[i])
{
minValue = array[i];
swapIndex = i;
}
}
if (swapIndex != -1)
{
swap(array, start, swapIndex);
}
++start;
}
}
else
{
while(start < end)
{
int swapIndex = -1;
int maxValue = array[start];
for (int i = start + 1; i < size; ++i)
{
if (maxValue < array[i])
{
maxValue = array[i];
swapIndex = i;
}
}
if (swapIndex != -1)
{
swap(array, start, swapIndex);
}
++start;
}
}
}- 선택정렬 요약 (오름차순)
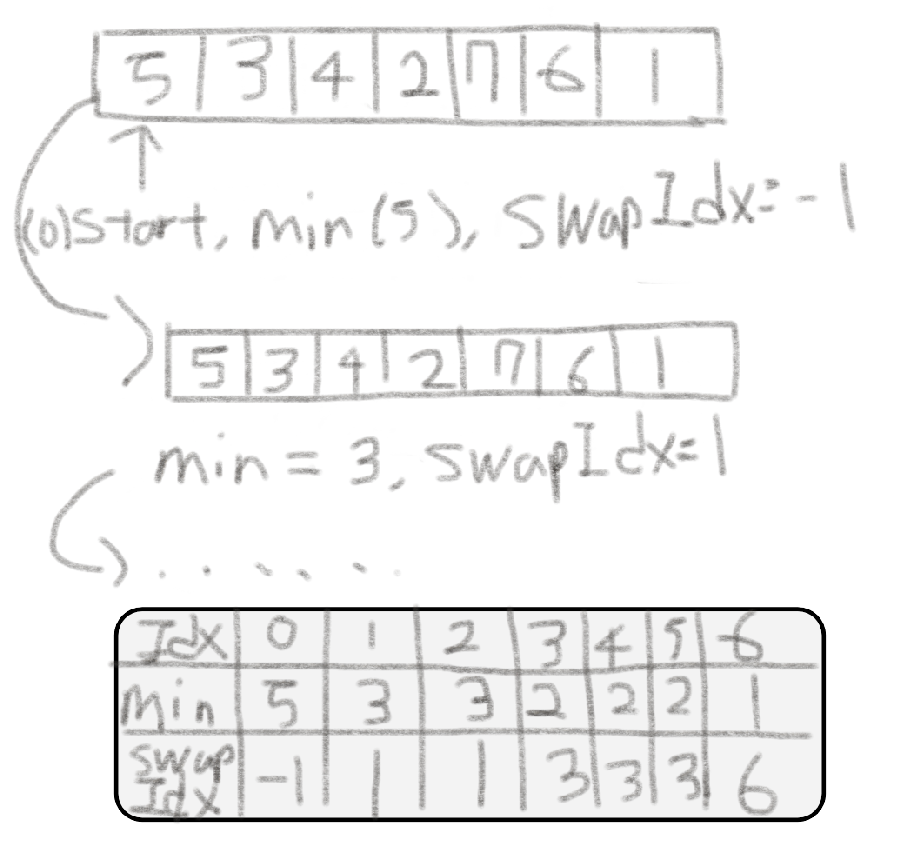
swapIdx가 -1이 아닌 경우에만 현재 start Index에 존재하는 값과 swapIdx에 존재하는 값을 서로 바꿔준다.
이를 반복하면 왼쪽부터 가장 작은 값이 채워진다.
3. 삽입 정렬
삽입 정렬 알고리즘 요약
- 손안의 카드를 정렬하는 방법과 유사하다.
- 새로운 카드를 기존의 정렬된 카드 사이의 올바른 자리를 찾아 삽입한다.
- 새로 삽입될 카드의 수만큼 반복하게 되면 전체 카드가 정렬된다.
- 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교 하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘
- 매 순서마다 해당 원소를 삽입할 수 있는 위치를 찾아 해당 위치에 넣는다.
삽입 정렬(insertion sort) 알고리즘의 구체적인 개념
- 삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬하는 알고리즘이다.
- 즉, 두 번째 자료는 첫 번째 자료, 세 번째 자료는 두 번째와 첫 번째 자료, 네 번째 자료는 세 번째, 두 번째, 첫 번째 자료와 비교한 후 자료가 삽입될 위치를 찾는다. 자료가 삽입될 위치를 찾았다면 그 위치에 자료를 삽입하기 위해 자료를 한 칸씩 뒤로 이동시킨다.
- 처음 Key 값은 두 번째 자료부터 시작한다.
구현
void insertionSort(int* array, int size, bool ascending)
{
// 1. 배열 사이즈가 1이하이면 정렬할 필요가 없음.
if (size < 2)
{
return;
}
int i, j, key;
if (ascending)
{
// 오름차순.
//
// 2. 배열의 두번째부터 선택
for (i = 1; i < size; ++i)
{
key = array[i];
for (j = i - 1; j >= 0 && array[j] > key; --j)
{
array[j + 1] = array[j];
}
array[j + 1] = key;
}
}
else
{
// 내림차순
for (i = 1; i < size; ++i)
{
key = array[i];
for (j = i - 1; j >= 0 && array[j] < key; --j)
{
array[j + 1] = array[j];
}
array[j + 1] = key;
}
}
}
- 삽입 정렬 요약 (오름차순)
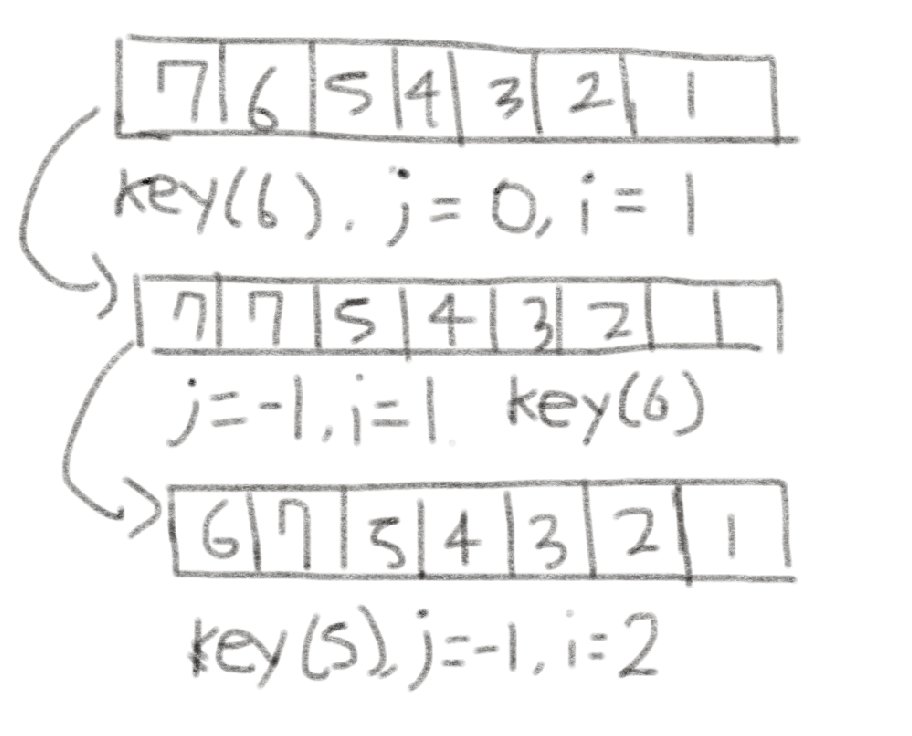
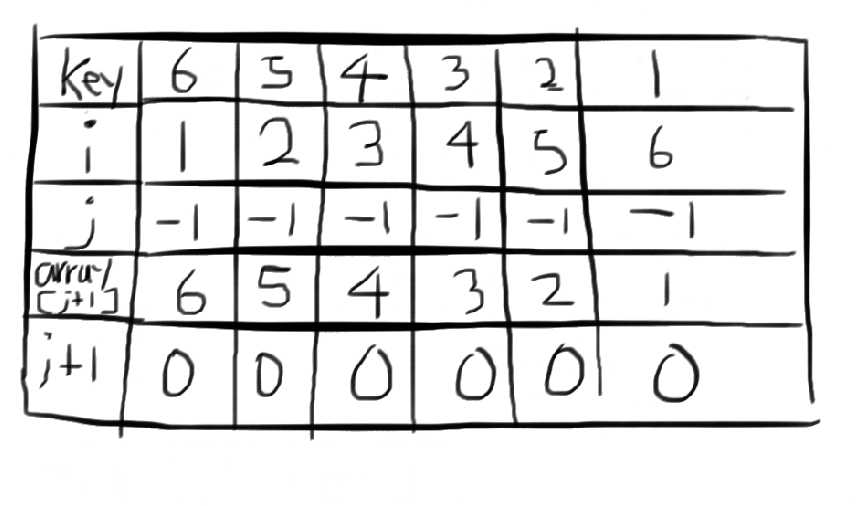
[ 7, 6, 5, 4, 3, 2, 1 ] 형태의 배열의 경우
key값이 i의 시작 index인 1에서 해당하는 값인 6부터 시작되고 6은 앞의 0번 인덱스까지 비교했을 때 6보다 작은 값이 나오지 않았으므로, 6과 7이 교환됩니다.
이러한 과정이 반복되어 예시로 key값이 4이고 i가 3인 경우에는 배열의 형태가 [5, 6, 7, 4, 3, 2, 1] 의 형태일 것인데, key는 4, i는 3이고 앞의 index 0, 1, 2가 가지고 있는 값은 4보다 작으므로,
array[3] = array[2] | array[2] = array[1]
| array[1] = array[0] 을 수행하면
[5, 5, 6, 7, 3, 2, 1]의 배열 형태가 되며, 배열의 끝까지 순회했으므로 j의 값은 -1이 됩니다.
key에 저장된 값을 array[j + 1] 에 제공하면 마지막으로 형태는 [4, 5, 6, 7, 3, 2, 1]의 형태가 됩니다.
이러한 과정을 반복하여 선택정렬이 수행됩니다.

정렬 정리해보면 뭔가 기본이 튼튼해지는 느낌이 들더라구용
잘읽었습니다!