파이프 옮기기 1

알고리즘 구분 : 다이나믹 프로그래밍

문제

유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의 번호이고, 행과 열의 번호는 1부터 시작한다. 각각의 칸은 빈 칸이거나 벽이다.

오늘은 집 수리를 위해서 파이프 하나를 옮기려고 한다. 파이프는 아래와 같은 형태이고, 2개의 연속된 칸을 차지하는 크기이다.

파이프는 회전시킬 수 있으며, 아래와 같이 3가지 방향이 가능하다.

파이프는 매우 무겁기 때문에, 유현이는 파이프를 밀어서 이동시키려고 한다. 벽에는 새로운 벽지를 발랐기 때문에, 파이프가 벽을 긁으면 안 된다. 즉, 파이프는 항상 빈 칸만 차지해야 한다.

파이프를 밀 수 있는 방향은 총 3가지가 있으며, →, ↘, ↓ 방향이다. 파이프는 밀면서 회전시킬 수 있다. 회전은 45도만 회전시킬 수 있으며, 미는 방향은 오른쪽, 아래, 또는 오른쪽 아래 대각선 방향이어야 한다.

파이프가 가로로 놓여진 경우에 가능한 이동 방법은 총 2가지, 세로로 놓여진 경우에는 2가지, 대각선 방향으로 놓여진 경우에는 3가지가 있다.

아래 그림은 파이프가 놓여진 방향에 따라서 이동할 수 있는 방법을 모두 나타낸 것이고, 꼭 빈 칸이어야 하는 곳은 색으로 표시되어져 있다.

가로

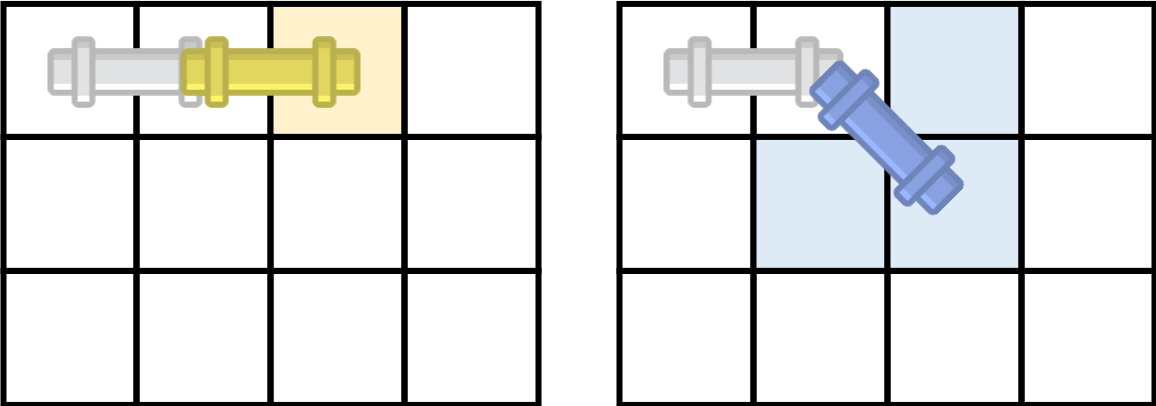
세로

대각선

가장 처음에 파이프는 (1, 1)와 (1, 2)를 차지하고 있고, 방향은 가로이다. 파이프의 한쪽 끝을 (N, N)로 이동시키는 방법의 개수를 구해보자.

입력
첫째 줄에 집의 크기 N(3 ≤ N ≤ 16)이 주어진다. 둘째 줄부터 N개의 줄에는 집의 상태가 주어진다. 빈 칸은 0, 벽은 1로 주어진다. (1, 1)과 (1, 2)는 항상 빈 칸이다.

출력
첫째 줄에 파이프의 한쪽 끝을 (N, N)으로 이동시키는 방법의 수를 출력한다. 이동시킬 수 없는 경우에는 0을 출력한다. 방법의 수는 항상 1,000,000보다 작거나 같다.

예제 입력 1
3
0 0 0
0 0 0
0 0 0
예제 출력 1
1
예제 입력 2
4
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
예제 출력 2
3
예제 입력 3
5
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
예제 출력 3
0
예제 입력 4
6
0 0 0 0 0 0
0 1 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
예제 출력 4
13

문제 풀이

파이프를 옮기는 과정에서 이전까지 옮겼던 방법의 수를 앞으로 옮길 때 포함해서 값을 더하여 가기에, 다이나믹 프로그래밍으로 구하는 문제라고 판단하였다. dp배열을 구현하는 과정에서, 방향성의 구분이 필요하기에 3차원배열(dp[17][17][3])으로 구현하였으며, 0은 가로 방향으로 놓여져 있는 경우, 1는 세로, 2는 대각선으로 구분하였다. 이렇게 구분한 뒤에, 문제에서 주어진 조건인, (1,1)과 (1,2)는 비어있다라는 조건과, 벽이 있을 경우 움직일 수 없다라는 조건들을 세세하게 덧붙여서 구현하면 되는 문제다.

소스 코드

#include <bits/stdc++.h>

using namespace std;

#define endl "\n"

int n;
int graph[17][17];
int dp[17][17][3]; // 가로 = 0, 세로 = 1, 대각선 = 2
void move(int x, int y, int dir); // 각 위치 및 방향별 움직이는 함수
void solve();

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    
    cin >> n;
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            cin >> graph[i][j];
        }
    }

    if(graph[n - 1][n - 1] == 1 || graph[0][0] == 1 || graph[0][1] == 1) {
        cout << 0 << endl;
    }
    else {
        memset(dp, 0, sizeof(dp)); // dp 배열 초기화
        dp[0][1][0] = 1;
        solve();
    }
    
    return 0;
}

void move(int x, int y, int dir) {
    if(dir == 0) {
        // 파이프 방향이 가로인 경우
        if(0 <= x && x < n && 0 <= y + 1 && y + 1 < n) {
            if(graph[x][y + 1] != 1) {
                dp[x][y + 1][0] += dp[x][y][dir];
            }
        }

        if(0 <= x + 1 && x + 1 < n && 0 <= y + 1 && y + 1 < n) {
            if(graph[x +1][y + 1] != 1 && graph[x + 1][y] != 1 && graph[x][y + 1] != 1) {
                dp[x + 1][y + 1][2] += dp[x][y][dir];
            }
        }
    
    }
    else if(dir == 1) {
        // 파이프 방향이 세로인 경우
        if(0 <= x + 1 && x + 1 < n && 0 <= y && y < n) {
            dp[x + 1][y][1] += dp[x][y][dir];
        }

        if(0 <= x + 1 && x + 1 < n && 0 <= y + 1 && y + 1 < n) {
            if(graph[x +1][y + 1] != 1 && graph[x + 1][y] != 1 && graph[x][y + 1] != 1) {
                dp[x + 1][y + 1][2] += dp[x][y][dir];
            }
        }
    }
    else if(dir == 2) {
        // 파이프 방향이 대각선인 경우
        if(0 <= x && x < n && 0 <= y + 1 && y < n) {
            if(graph[x][y + 1] != 1) {
                dp[x][y + 1][0] += dp[x][y][dir];
            }
        }

        if(0 <= x + 1 && x + 1 < n && 0 <= y + 1 && y < n) {
            if(graph[x +1][y + 1] != 1 && graph[x + 1][y] != 1 && graph[x][y + 1] != 1) {
                dp[x + 1][y + 1][2] += dp[x][y][dir];
            }
        }

        if(0 <= x + 1 && x + 1 < n && 0 <= y && y < n) {
            if(graph[x +1][y] != 1) {
                dp[x + 1][y][1] += dp[x][y][dir];
            }
        }
    }

}

void solve() {
    int result = 0;

    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            if(i == 0 && j == 0) {
                continue;
            }
            
            for(int k = 0; k < 3; k++) {
                if(graph[i][j] != 1) {
                    move(i, j, k);
                }
            }
        }
    }

    result = dp[n - 1][n - 1][0] + dp[n - 1][n - 1][1] + dp[n - 1][n - 1][2];

    cout << result << endl;
}

• 문제 출처 : https://www.acmicpc.net/problem/17070
• 해당 풀이는 백준에서 "맞았습니다"" 판정을 받았습니다.