도넛과 막대 그래프
문제 출처: https://school.programmers.co.kr/learn/courses/30/lessons/258711?language=cpp
문제 풀이 과정
예제 풀이 1
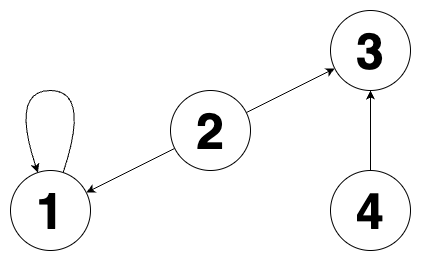
예제는 이미지로 구조화되어 있기에, 직관적으로 파악할 수 있다. 2번이 생성 노드임을 알 수 있다.
예제 풀이 2
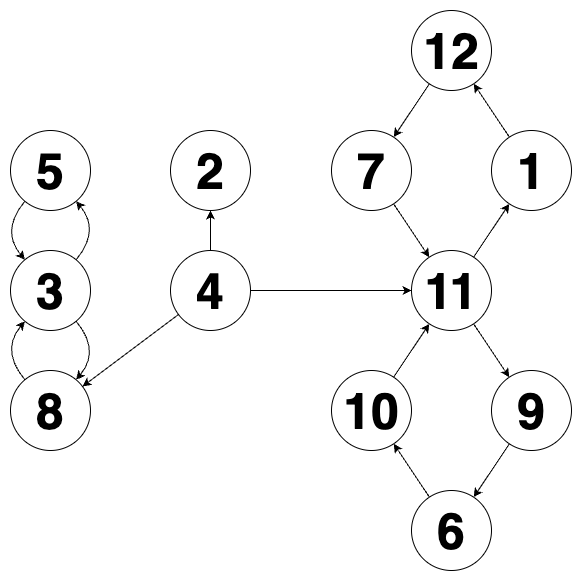
예제는 이미지로 구조화되어 있기에, 직관적으로 파악할 수 있다. 4번이 생성 노드임을 알 수 있다.
접근 과정
예제 2개에서 공통적으로 찾을 수 있는 특징으로는 생성 노드가 목적지가 되는 경우가 없다는 것이다. 문제의 내용에서도 관련된 내용을 찾을 수 있다. 문제에서 보면, 그래프들과 무관한 정점을 하나 생성한 뒤, 각 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 임의의 정점 하나로 향하는 간선들을 연결했습니다.라고 되어있다. 즉, 생성한 노드가 간선의 출발 노드가 된다는 것이다.
그렇기에, 각 노드가 목적지가 되는 횟수를 배열로 가지고 있으면서, 이것이 0일 대 생성한 노드가 될 수 있는 첫 번째 조건으로 활용하면 된다.
두 번째 생성 노드 조건은 문제를 잘 읽어보면 찾을 수 있다. 문제 제한사항을 살펴보면, 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 수의 합은 2이상입니다.라는 문장이 있다. 이 문장이, 두 번째 생성 노드와 관련된 조건이다. 즉, 생성 노드가 출발 노드인 간선이 2개 이상 존재한다는 것이다.
두 번째 조건이 중요한 이유는 막대 모양 그래프를 통해 확인할 수 있다.
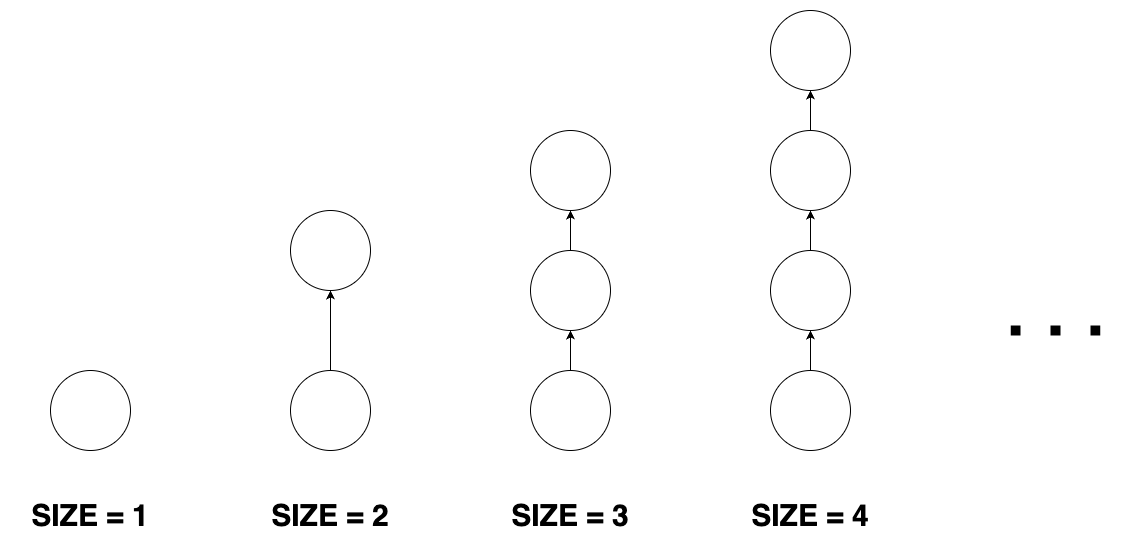
막대모양 그래프의 SIZE=1인 모양 그래프를 보면, 출발지가 되는 경우와 목적지가 되는 경우가 모두 0이다. SIZE>=2인 그래프들 또한 목적지가 되는 경우가 0이면서 출발지가 되는 경우가 1인 노드가 존재한다.
두 번째 조건이 없다면, 막대모양 그래프의 일부인지 생성한 노드인지를 판단할 수 없는 것이다.
이렇게 생성한 노드를 찾은 이후에는, 생성한 노드로부터 연결된 각 노드들이 어떠한 모양 그래프의 포함되는지를 판단하면 된다.
도넛 모양 그래프의 특징을 정리하면 다음과 같다.
- 각 노드가 출발지가 되는 경우, 목적지가 되는 경우가 무조건 1번이다.
막대 모양 그래프의 특징을 정리하면 다음과 같다.
- 막대 모양 그래프의 노드 중 하나는 출발지 노드로는 1번, 목적지 노드로는 0번이 된다. (생성한 노드와 연결되는 경우를 제외하면)
8자 모양 그래프의 특징을 정리하면 다음과 같다.
- 8자의 중심이 되는 노드는 출발지 노드로 2번, 목적지 노드로 2번이 되어야 한다. (생성한 노드와 연결되는 경우를 제외하면)
위 세 가지 특징 중에서, 판단하기 제일 어려운 것이 도넛 모양 그래프라고 생각했다. 순환되는 도넛 모양 전체를 한 바퀴 돌아야만 판단이 가능하기 때문이다.
그렇기에, 생성한 노드와 간선으로 연결된 노드에서 모양 그래프를 판단할 때, 기본적으로 도넛 모양으로 가정한 이후, 막대 모양이나 8자 모양에 해당하는 특징을 가진 노드가 있다면, 해당 모양을 의미하도록 변경하는 방식을 취했다.
최종 로직
- 주어진 input을 노드별 목적지를 가지도록 변경하여 저장
- 생성한 노드를 찾기
- 생성한 노드와 연결된 노드 순회 진행
- 도넛 모양을 기본 설정으로 잡은 뒤, 막대 모양과 8자 모양의 특징에 해당하는 노드가 등장할 경우, 모양 변경
- 연결된 모든 간선 순회했다면, 최종 모양으로 answer 배열 업데이트
- 3~5의 과정을 모든 연결된 노드에서 진행
정답 코드
#include <bits/stdc++.h>
using namespace std;
vector<int> solution(vector<vector<int>> edges) {
vector<int> answer(4); // 순서: 생성한 정점의 번호, 도넛 모양 그래프의 수, 막대 모양 그래프의 수, 8자 모양 그래프의 수
vector<int> graph[1000001];
int dest_cnt[1000001]; // 노드가 목적지가 된 횟수 계산
set<pair<int, int>> visited;
// 방문 배열 초기화
memset(dest_cnt, 0, sizeof(dest_cnt));
int max_idx = 0;
for(auto edge: edges) {
graph[edge[0]].push_back(edge[1]);
dest_cnt[edge[1]]++;
// 최대 index 확인 위한 업데이트
max_idx = max(max_idx, edge[0]);
max_idx = max(max_idx, edge[1]);
}
// 생성 노드 찾기
for(int i = 1; i < max_idx + 1; i++) {
if(dest_cnt[i] == false && graph[i].size() >= 2) {
answer[0] = i;
break;
}
}
// 생성 노드 기준으로 그래프 모양 찾기
for(auto node: graph[answer[0]]) {
visited.insert({answer[0], node}); // 방문 처리 (앞으로 미사용)
dest_cnt[node]--; // 목적지 횟수 감소
int node_type = 1; // 1: 도넛 모양, 2: 막대 모양, 3: 8자 모양
queue<int> q;
q.push(node);
while(!q.empty()) {
int now = q.front();
q.pop();
// 막대 모양
if(dest_cnt[now] <= 1 && graph[now].size() == 0) {
node_type = 2;
break;
}
// 도넛 모양
if(dest_cnt[now] == 2 && graph[now].size() == 2) {
node_type = 3;
break;
}
for(auto next: graph[now]) {
if(visited.find({now, next}) == visited.end()) {
visited.insert({now, next});
q.push(next);
break;
}
}
}
answer[node_type]++;
}
return answer;
}느낀 점
Lv2이지만, 개인적으로는 정말 어렵게 느껴졌던 문제였다. 2시간을 넘게 고민하면서, 해설을 일부 참고하기도 했다.
문제에서 특징을 찾아내고, 정리하는 과정에서 부족함을 많이 느꼈다.

