Recursion : 회귀

이전의 결과를 활용하여 현재의 결과를 도출하는 알고리즘

A suitable method for circular definition

Recursion Structure

1. recursive call을 만드는 파트

ex) return n * factorial(n-1);

2. recursive call을 멈추는 파트

ex) if (n <= 1) return 1;

If there is no part that stops the recursive call, it is called continuously until a system error occurs

Recursion Principle

Devide-and-conquer

• Divide the problem into a set of sub-problems
• sub-problems의 수는 1 이상이어야 함

Recursion vs Iteration

대부분의 recursion은 iteration으로 표현(실행) 가능

Recursion

• pros : good choice for recursive problems (easy to implement)
• cons : overhead of function calls → usually slower execution time

Iteration

• pros : fast execution time
• cons : programming can be often very difficult for recursive problems

이러한 장단점들로 인하여 문제에 따라 무엇이 더 나은 방법인지 나뉨

ex 1) Factorial computation

• time complexity : recursion = iteration
• memory and call overhead : recursion > iteration
• total complexity : recursion > iteration

→ iteration is better choice

ex 2) Power computation

• time complexity : recursion < iteration
• memory and call overhead : recursion > iteration
• total complexity : recursion < iteration

→ recursion is better choice

ex 3) Fibonacci computation

• time complexity : recursion > iteration
• memory and call overhead : recursion > iteration
• total complexity : recursion > iteration

→ iteration is better choice

Examples of Recursion

1. Factorial

Iterative implementation

Recursive implementation

unsmart way

Time complexity of implementation(with n inputs)

Time complexity of recursion

2. Power Computation

Iterative implementation

Recursive implementation

1. pseudo code
   

• when n is even, power(x,n) = power(x², n/2)
• when n is odd, power(x,n) = power(x², (n-1)/2)

2. C code
   

Time complexity 비교

T(n) = xT(yn) + c
→ sub problem의 개수가 x배, size of subproblem이 y배가 됨
※ x == y인 경우, time complexity에는 변화가 없음

power computation에서는 recursive 사용하여 sub problem의 개수는 유지한 상태에서 size를 1/2로 줄임!

참고

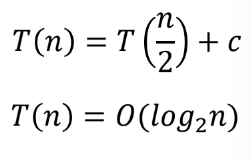
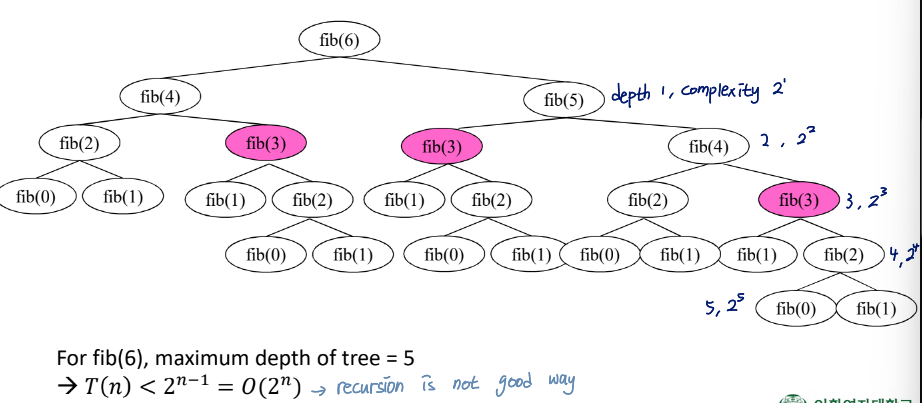
3. Fibonacci Series

Iterative implementation

Time complexity of implementation(with n inputs)

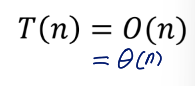
Recursive implementation

size 변화 없이 문제의 개수만 늘어서 비효율적임

Time complexity of recursion

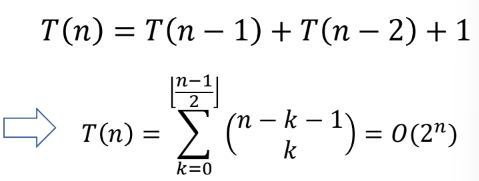
대학원에서 더 자세히 알 수 있다고 함

Why is the recursion is inefficient for Fibonacci Series?

cuase the same terms are computed in dupliate

4. Hanoi Tower

Procedure

1. move n-1 discs from A to B
2. move n-th disc from A to C
3. move n-1 discs from B to C

Pseudo code

Code

Time complextity

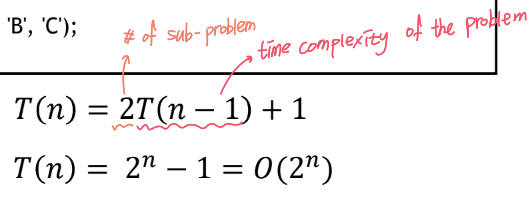
5. Binary Search

순서대로 나열된 숫자들의 집합 중 특정한 수의 인덱스를 찾고자 함

• input : a set of ordered numbers {a1,...,an}
• goal : query b
• output : an index k where ak = b_

Iterative implementation

Time complexity of implementation(with n inputs)

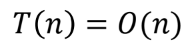
Recursive implementation

Time complexity of recursion

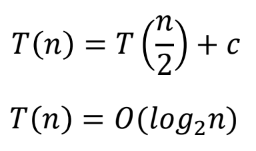
problem size는 절반으로 줄고 problem의 개수는 유지함

Recursion Types

1. Tail recursion

can be easily implemented using iteration
Ex) return n * factorial(n-1);

2. Head recursion

difficult to implement using iteration
Ex) return factorial(n-1) * n;

3. Multi-recursion

difficult to implement using iteration
Ex)

if-else를 통해 각각에서 recursion을 사용하는 것은 multi-recursion이 아님!!!!