문제 출처: 코드잇

---

❗1차 실패

구상 1시간 47분

---

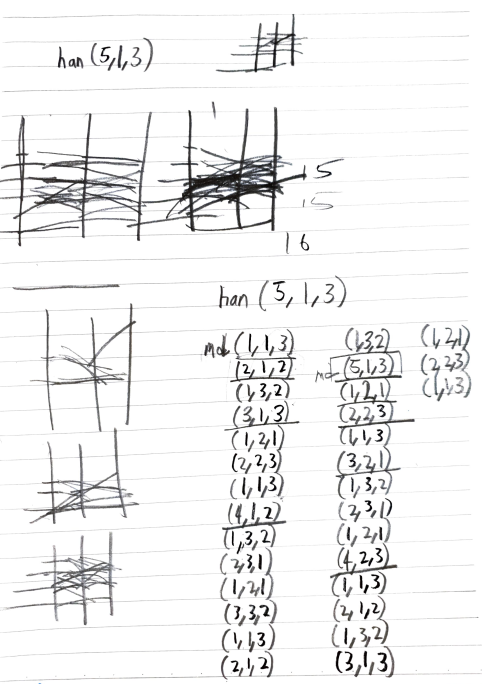
2차 성공(힌트참고)

깨달음을 주는 힌트 30분

출처: 코드잇

1. 가장 큰 원판을 제외하고 나머지 원판들을 start_peg에서 other_peg로 이동
2. 가장 큰 원판을 start_peg에서 end_peg로 이동
3. 나머지 원판들을 other_peg에서 end_peg로 이동

구상 15분

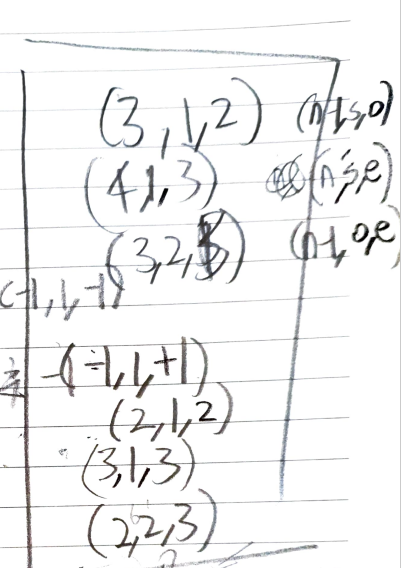
구현 15분

def move_disk(disk_num, start_peg, end_peg):
    print("%d번 원판을 %d번 기둥에서 %d번 기둥으로 이동" % (disk_num, start_peg, end_peg))

def hanoi(num_disks, start_peg, end_peg):
    # 코드를 입력하세요.
    # base case
    if num_disks == 0:
        return
    
    other_peg = 6 - (start_peg + end_peg) # 남은 기둥 위치 구하기
    # recursive case
    hanoi(num_disks-1,start_peg, other_peg) # 제일큰 원판 목표지점 이동전 other_peg에 순차적으로 쌓아두는 함수 
    move_disk(num_disks, start_peg, end_peg) # 제일큰 목표지점으로 이동
    hanoi(num_disks-1,other_peg, end_peg)# 제일큰 원판 목표지점 이동후 순차적으로 쌓아둔 원판들 제일큰 원판 위로 다시 이동

# 테스트 코드 (포함하여 제출해주세요)
hanoi(3, 1, 3)

다음 재귀함수 구상시 팁이 될 것 같은 생각?

• 진부할 수도 있지만 같은 함수를 호출 하는 것이니 사이즈가 더 작게 되는 똑같은 형식을 다시 활용 한다고 생각을 이미지화 하고 풀어 볼것
  

느낀점

하노이의 탑풀이는 마치 피타고라스의 정의에 대한 원리를 해설 없이 이해하는 과정과 같은 느낌이 들었다. 문제해결 능력을 기르려면 가능한 힌트나 답안을 참고 하지 않는 것이 여러가지 각도 및 깊이 파고들어 생각 할 수 있는 능력이 길러 지기 때문에 장기적으로 좋을 것 같으면서도 확신은 서지 않는다.