문제

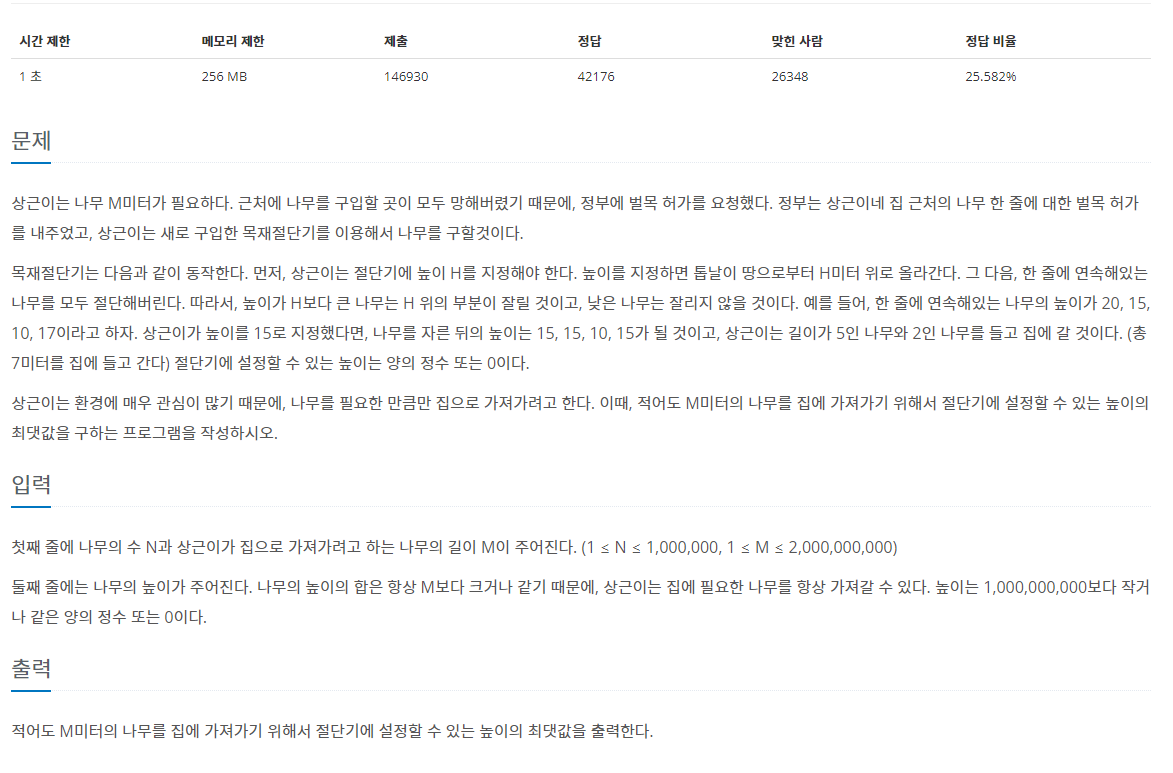
입력

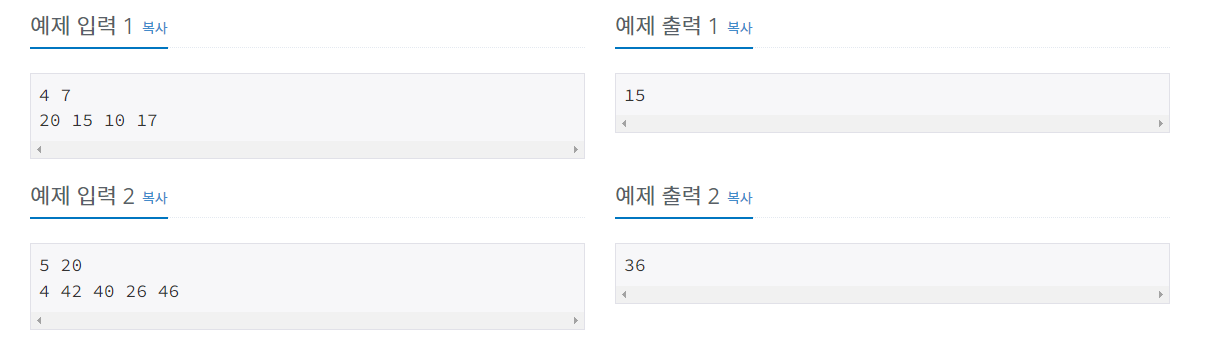
풀이

첫 시도

public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();//나무 수
        int M = sc.nextInt();// 나무 가져가고싶은 길이
        int[] trees = new int[N];```

        int result=0;
        for(int i=0; i<N; i++){
            trees[i] = sc.nextInt();
            if(result<trees[i]){
                result=trees[i];
            }
        }
        while(true){
            int count=0;//가져갈려는 길이
            for(int i=0; i<N; i++){
                if(trees[i]/result>=1){
                    count += trees[i]%result;
                }
            }
            if(count==M) {
                break;
            }
            result--;
        }
        System.out.println(result);
    }

1. 처음엔 나무들을 배열로 나열하면서 result 변수에 가장 큰 수를 받는다.
2. while문에 count에 나무 1씩 가져가는 형식으로 해서 만약 M(나무 가져가고 싶은 길이)과 일치한다면, while문을 멈추는 형식으로 했다.
3. 그리고 if문은 result보다 작은 나무는 자를 필요없기때문에 나눴을때 1 이상이면, 잘라도 되는 나무로 보는형식으로 했다.

출력 값은 같으나, 시간 초과가 되면서 틀렸다. 다른 방식을 써야했다.

두번째 시도

이 문제를 주신 스터디장님이 이진 탐색을 참고해봐라. 해서 찾아보았다.

참고 : https://yoongrammer.tistory.com/75

이걸 보고

public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();//나무 수
        int M = sc.nextInt();// 나무 가져가고싶은 길이
        int[] trees = new int[N];```

        int result=0;
        for(int i=0; i<N; i++){
            trees[i] = sc.nextInt();
            if(result<trees[i]){
                result=trees[i];
            }
        }
        int[] temp = int[result];
        
        for(int i=0 ; i<result; i++{
        temp[i] = i;
        }
        int low =0;
        int high = result-1;
        

처음엔 temp배열을 하나하나 할당을 해 이 배열로 이진 탐색을 해 찾을려고 했다.
근데 문제점은
1. 너무 시간이 오래 걸린다.
-> for문을 또 여러개 쓰고, 찾는데 너무 오래걸린다.
2. 이진 탐색 조건이 너무 애매하다
-> 나무 자른걸 다 합쳐서 M변수와 비교해가면서 low,high를 줄여나가야 하는데 굳이 temp 배열에 0~result까지 배열 숫자를 넣고 할 필요가 없다. 그리고 비교를 할때 너무 많은 연산이 들어간다.

그래서 다 지웠다.

세번째 시도

여기선 너무 감이 안와 검색을 해보았습니다.

참고 : https://st-lab.tistory.com/270

여기선 아주 간단하게 해결했습니다.

import java.util.*;

public class ex_2805 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();//나무 수
        int M = sc.nextInt();// 나무 가져가고싶은 길이
        int[] trees = new int[N];
        int high = 0;
        int low=0;
        for (int i = 0; i < N; i++) {
            trees[i] = sc.nextInt();
            if (high < trees[i]) {
                high = trees[i];
            }
        }
        //2진 탐색
        while(low<high){
            int mid = low +(high-low)/2;
            long sum =0;
            //나무 자를것들 다 더하기
            for(int i=0;i<trees.length;i++){
                //음수는 자르는 위치보다 작은 나무이기 때문에 패스한다.
                if(trees[i]-mid>0){
                    sum+=(trees[i]-mid);
                }
            }
            //자른 나무 합이 M보다 작은건 자르는 위치가 높은거기때문에 높이를 낮춰야 하기때문에 high를 낮춘다.
            if (sum < M) {
                high=mid;
            }
            //자른 나무 합이 M보다 작은건 자르는 위치가 낮은거기 때문에 덜 잘라야한다. 그래서 높이를 올리기 위해 low를 올린다.
            else{
                low = mid+1;
            }
        }
        System.out.println(low-1);
    }
}

1. 배열에 나무들 나열한건 같으나 mid,high,mid를 배열에서만 쓴다고 생각했었는데,
   그냥 int형으로 써도 된다는걸 알았습니다.
2. sum을 통해 나무 자른것들 다 더해서 M과 비교해 low,high의 숫자를 변경해온다.
3. 마지막 low는 high보다 높으면 탐색이 실패한 경우 이다.-> 탐색 종료시점
4. low-1을 해서 출력하는 이유는 탐색 종료 시점에서 탐색값을 초과해서 처음 만나는 값이 되기 때문에,
   -1을 한다. -> upperBound방식

   참고 :UpperBound 방식을 사용하여 하면, 원하는 탐색값의 +1이 되기 때문에 실제로 만족하는 값은 Upper Bound를 통해 반환 된 값의 -1을 한 값이 만족하는 값이 된다.

배운점

이진 탐색 형식 문제를 풀다보면 이 방식을 찾은 사람은 정말 천재인거 같습니다.
이진 탐색은 꼭 배열형식으로 안해도 인덱스값으로 mid,max,min 형식을 할수 있다.
이진 탐색 구현한 코드를 이해했습니다.