Stack
입,출력을 한 방향으로만 할수있는 자료구조이다.
- LIFO(Last In First Out)을 따름.
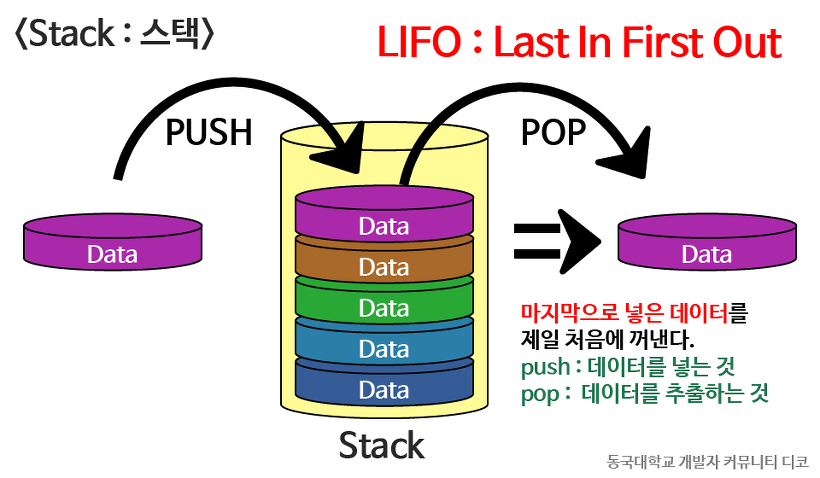
출처 : https://blog.geusan.com/29
Stack 연산
- push() : 스택에 데이터 추가한다.
- pop() : 가장 나중에 추가된 데이터를 스택에서 삭제하고 삭제한 데이터를 리턴한다.
- size() : 스택에 추가된 데이터의 크기를 리턴한다.
- peek() : 가장 최근에 추가된 데이터를 리턴한다.
- show() : 현재 스택에 들어있는 모든 데이터를 String타입으로 변환하여 리턴한다.
- clear() : 현재 스택에 들어있는 모든 데이터들을 삭제한다.
- empty() : Stack이 비어 있으면 true, 아니면 false를 반환한다.
Stack 사용
스택은 연결리스트로 구현할 수 있다.
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(2);
stack.push(3);
System.out.println(stack.peek()); // stack의 가장 상단의 값 출력
stack.pop(); // stack에 값 제거
stack.clear(); // stack의 전체 값 제거 (초기화)Stack 사용 예
- 재귀 알고리즘 : 재귀 행위들을 직관적으로 가능하게 해준다.
- 웹 브라우저 방문기록(뒤로,앞으로가기)
- 실행 취소 (ctrl + z)
Queue
먼저 들어온 데이터가 먼저 빠지는 구조이다.->FIFO(First-In-First-Out)
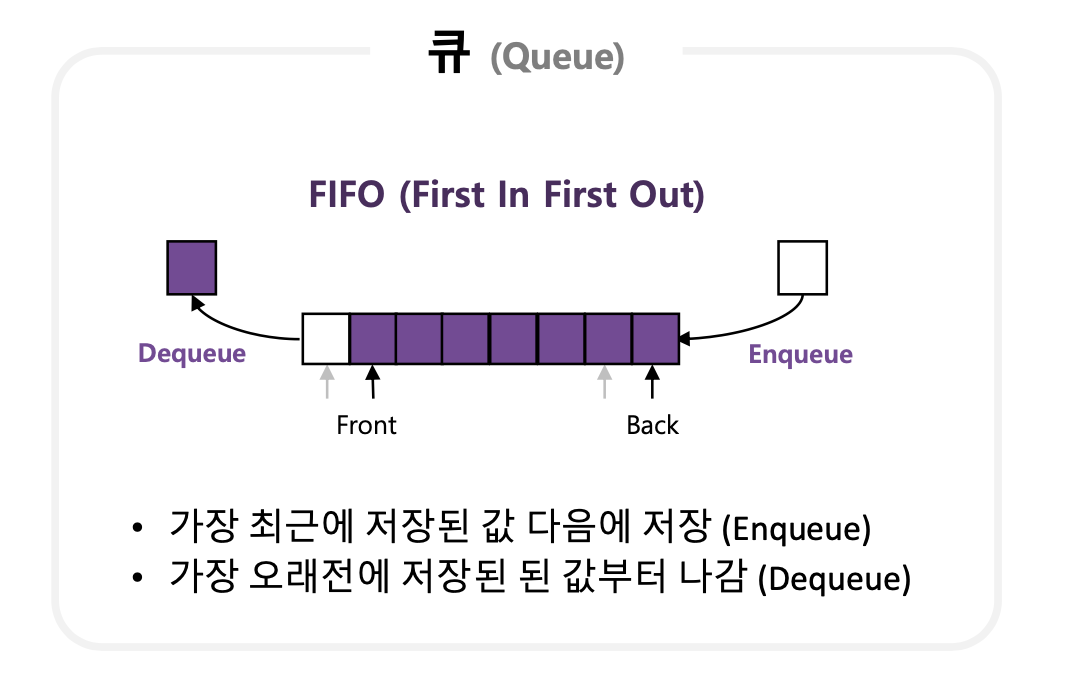
출처 : https://velog.io/@awesomeo184/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%81%90Queue
Queue 연산
- add() : 큐에 데이터를 추가한다.
- poll() : 가장 먼저 추가된 데이터를 큐에서 삭제하고, 삭제한 데이터를 리턴한다.
- size() : 큐에 추가된 데이터 크기를 리턴한다.
- peek() : 큐에 가장 먼저 추가된 데이터를 리턴한다.
- show() : 큐에 들어있는 모든 데이터를 String 타입으로 변환해서 리턴한다.
- clear() : 큐에 들어있는 모든 데이터를 삭제한다.
Queue 사용
Queue 클래스는 인터페이스이기 때문에 객체 생성할땐 LinkedList 클래스를 사용해야한다.
Queue<Integer> queue = new LinkedList<>();
queue.add(1); // 1 넣음
queue.add(2); //2 넣음
queue.size(); //2
queue.poll(); // 2 꺼내짐Tree
- 비선형 자료구조이다.
-> 노드들의 계층적 관계를 표현한다.
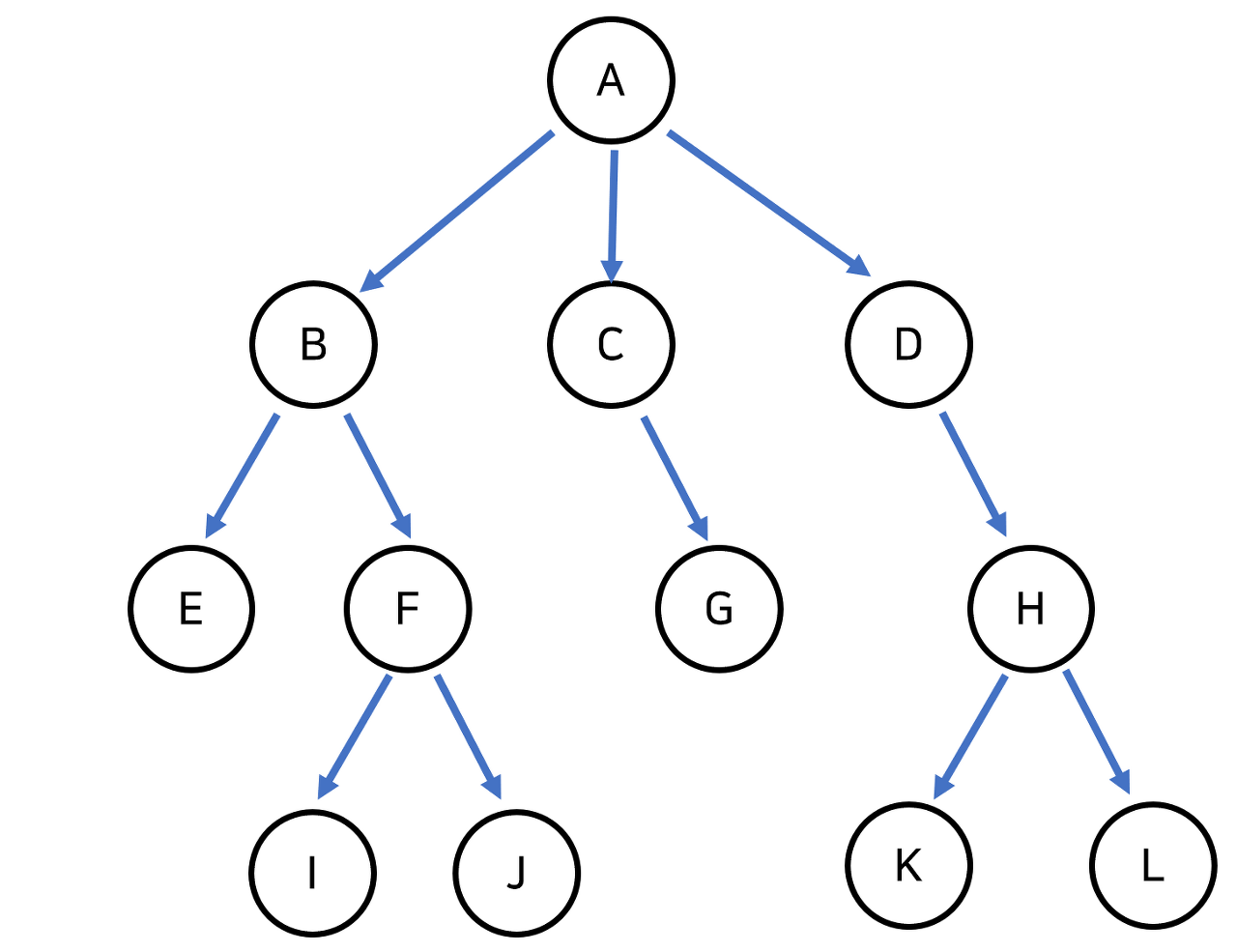
출처 : https://currygamedev.tistory.com/19
Tree 구조와 용어
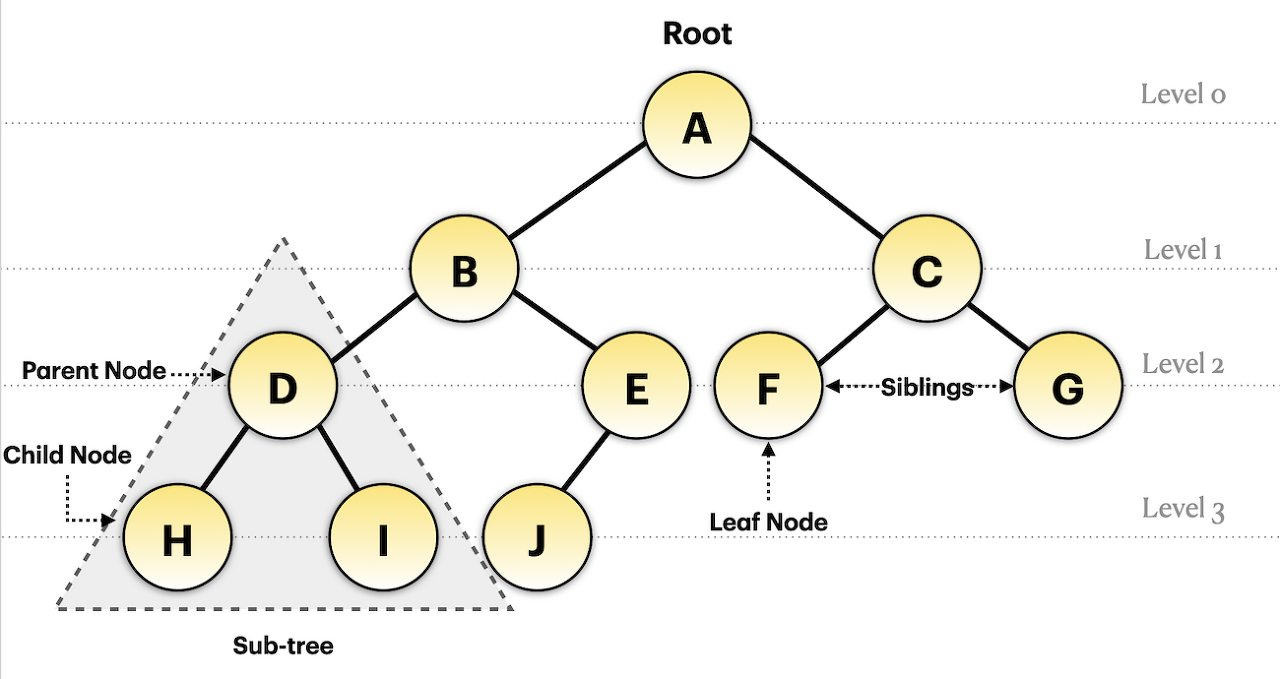
출처 :https://yunamom.tistory.com/249
- node
트리를 구성하는 기본요소.
노드엔 데이터와 하위 노드에 대한 참조를 가지고 있다. - Root node(뿌리) : 최상위 루트. 이 노드는 하나만 가진다.
- Leaf node(잎) : 자식이 없는 맨 마지막 노드
- Sibling node(형제) : 같은 부모를 가지는 노드
- Parent node(부모) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
- Child node(자식) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
- Subtree :A 루트 기준으로 B로 가면 왼쪽 서브 트리, C로 가면 오른쪽 서브트리라고한다.
- Edge(선) : 노드와 노드를 이어주는 선
- Height(높이) : 루트 노드에서 가장 깊숙히 있는 리프 노드 까지 높이
- depth(깊이) : 루트노드에서 특정 노드까지 가는데 사용하는 간선의 수.
- level(레벨) : 같은 깊이를 가지고 있는 노드를 묶어서 레벨이라 한다.
Graph(그래프)
- 요소들이 서로 복잡하게 연결되어 있는 관계를 표현하는 자료구조이다.
- 정점,간선들의 집합이다.
그래프 용어
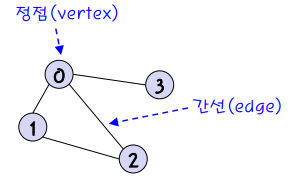
출처 : https://suyeon96.tistory.com/32
- 정점(vertex) : 노드라고도 부르고, 데이터가 저장되는 그래프의 기본 원소이다.
- 간선(edge) : 정점 간의 관계를 나타낸다.
- 인접 : 두 정점을 연결하는 간선이 있을때 이 두 정점은 인접하다 한다.
- 인접 정점 : 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점
- 진입차수(in-degree),진출차수(out-degree) : 한 정점에 들어가고 나가는 간선이 몇개인지 나타내는 것
- 자기 루프(self loop) : 간선이 자기자신으로 진입하는 경우

- 사이클 : 시작 정점과 종료 정점이 같은 단순 경로를 뜻한다.
그래프 종류
간선의 종류에 따라 구분된다.
무방향 그래프,방향 그래프
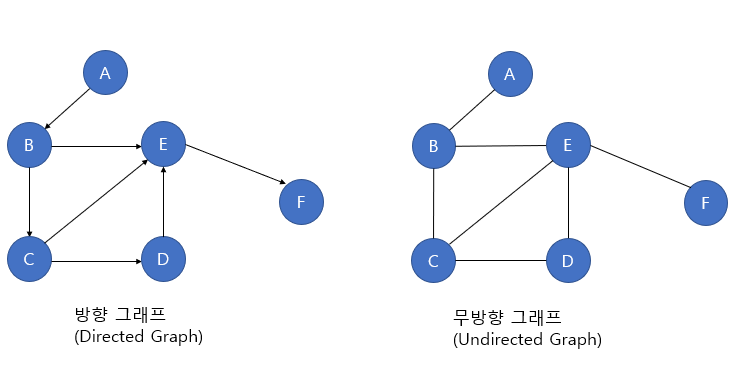
출처 : https://code-lab1.tistory.com/13
무방향 그래프 : 두 정점을 연결하는 간선에 방향이 없고 양 방향이다.
방향 그래프 : 간선의 방향으로만 이동할수 있다.
가중치 그래프
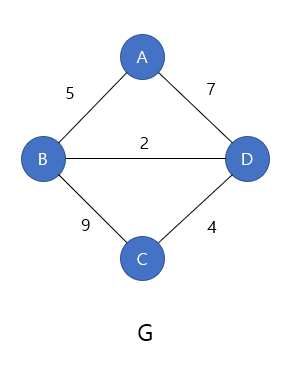
출처 : https://code-lab1.tistory.com/13
간선에 가중치,비용(cost)가 부여 되어 있는 그래프이다.
->예를 들어 서울에서 부산까지 몇km 나타낼때
그래서 네트워크라고 부르기도한다.
완전 그래프
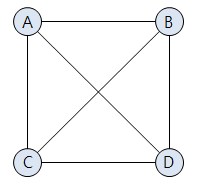
출처 : https://suyeon96.tistory.com/32
모든 정점 간에 간선이 존재하는 그래프
그래서 정점의 수가 n이라면, 전체 간선의 수는 n(n-1)/2가 된다.
위 그래프는 n=4이기에 간선의 수는 (43)/2=6. 6개다
그래프의 표현 방식
구현하는 방법엔 Array와 Linked List로 구현하는 방법이 있다.
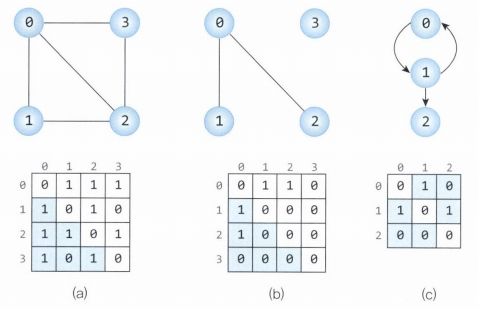
인접 행렬을 이용한 그래프 구현
출처 : https://suyeon96.tistory.com/32
그래프의 정점을 2차원 배열로 만든것이다.
정점의 개수를 n으로 하면 n*n 행렬로 각 원소들은 정점간의 간선을 나타낸다.
간선이 존재하는 두 정점 인덱스에는 1로 없는 칸은 0으로 채우고 만약 가중치가 다른 그래프라면 해당 가중치를 넣어준다
장점으로는
- 모든 정점들의 간선 정보가 있어서, 두 정점을 연결하는 간선을 조회할때
O(1)시간 복잡도로 가능하다. - 구현이 간단하다.
단점은 - n*n 2차원 배열이기때문에 메모리가 많이 필요하다
- 모든 간선 정보를 대입하는데 시간이 걸린다.
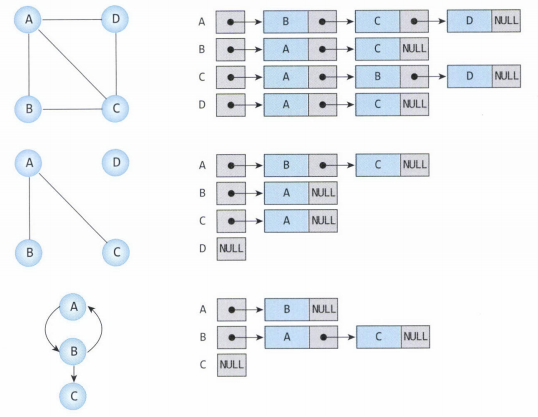
인접 리스트를 이용한 그래프 구현
출처 :https://suyeon96.tistory.com/32
각 정점에 인접한 정점들을 연결리스트로 표현하는 방법이다.
메모리를 효율적으로 사용하고 싶을때 사용한다.
장점
- 인접 행렬 보다 메모리 사용엔 효율적이다.
- 모든 간선을 알아내기 위해 각 정점의 헤더 노드부터 모든 인접 리스트를 탐색해야 하므로
O(n+e)의 시간이 소요된다.
단점
- 두 정점을 연결하는 간선을 조회하거나 정점의 차수를 알기위해선 정점의 차수만큼 시간이 필요하다 ->
O(degree(v))
구현이 어렵다.
참고
https://currygamedev.tistory.com/19
https://suyeon96.tistory.com/32
