Euler Tour Technique

Euler Tour Technique에 대해 간단히 설명하고 넘어가려고 한다.

아래와 같은 트리가 있다고 하자

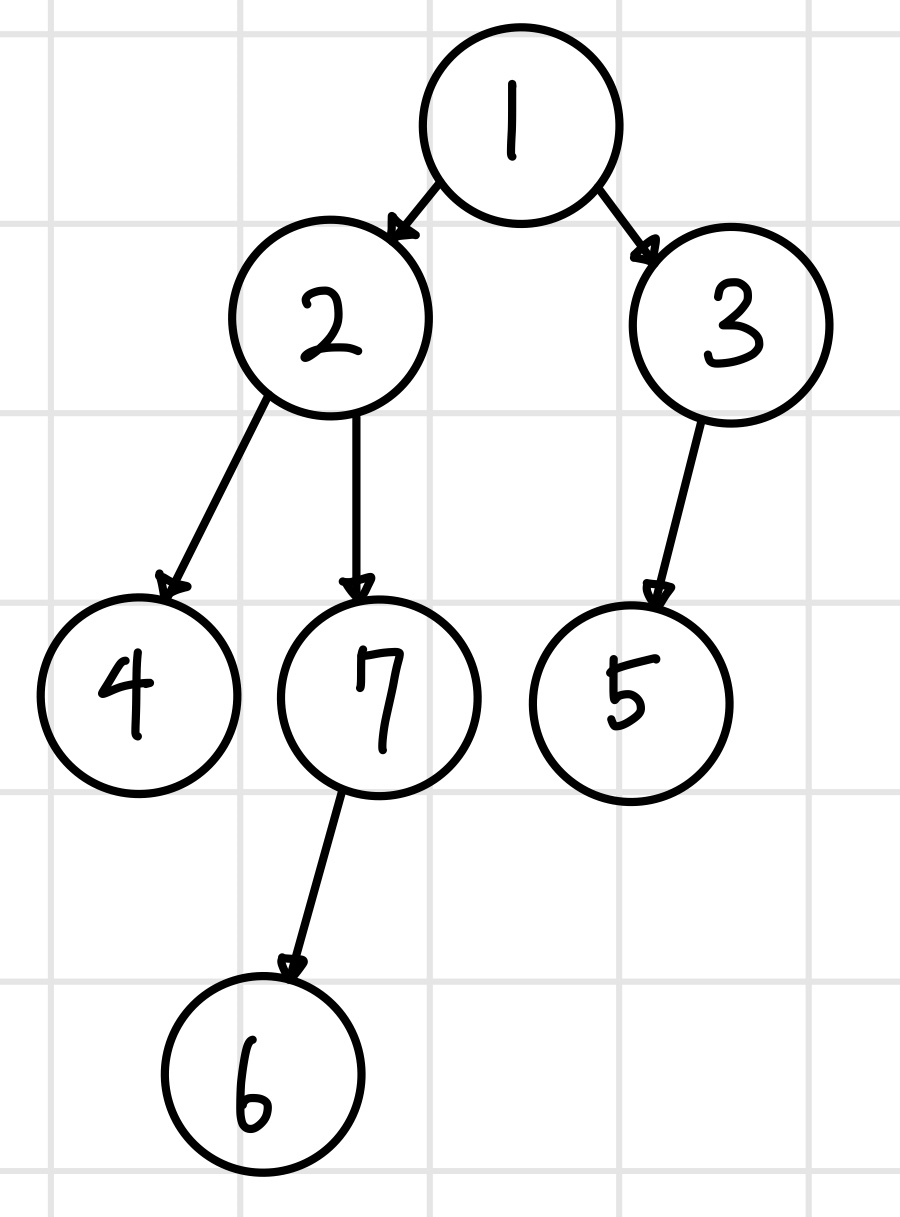
루트 노드부터 DFS를 돌려서 각 노드가 방문되는 순서로 번호를 붙여준다.

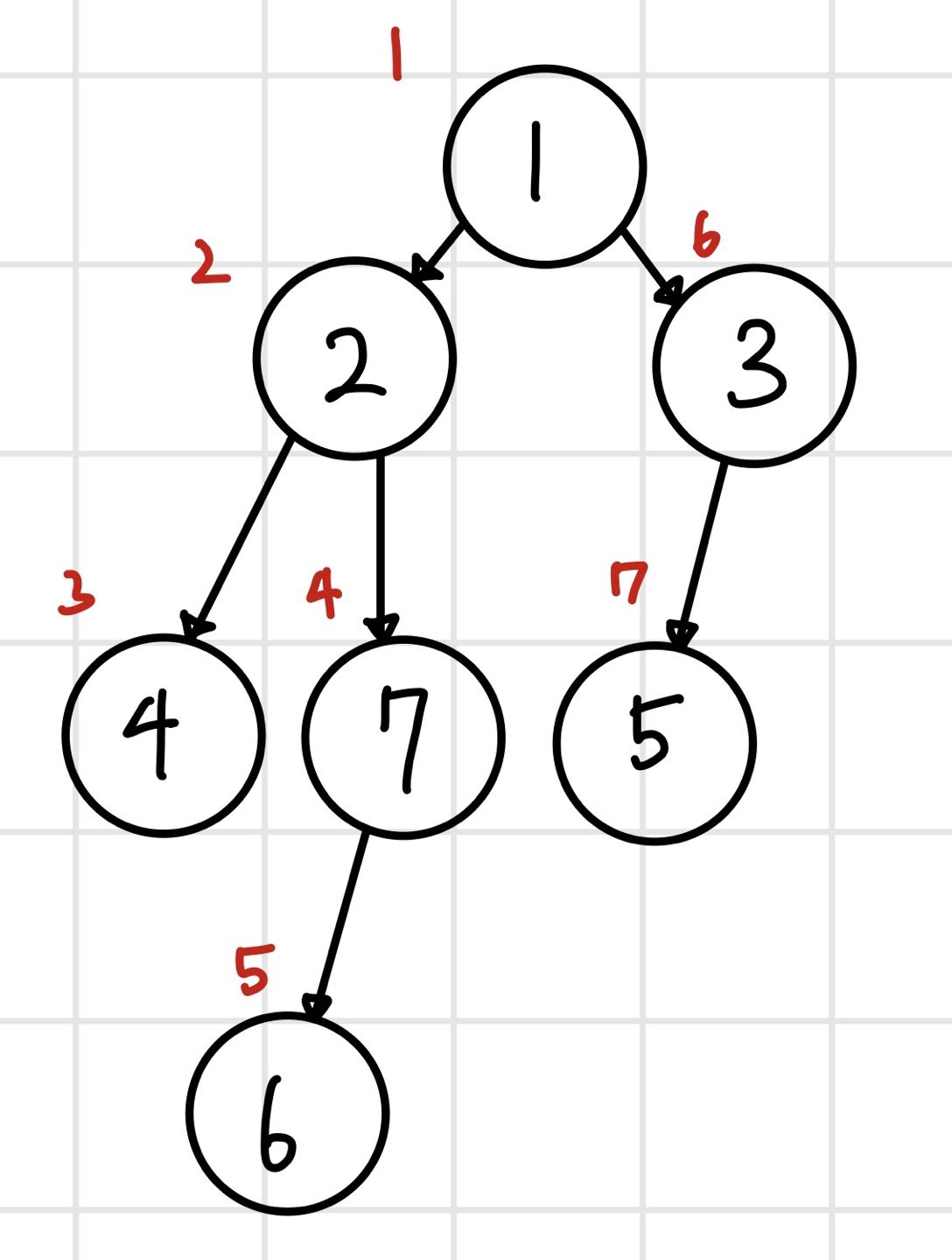
번호를 붙여주게 되었을 때 아래와 같은 Table이 나온다.

탐색 순서	1	2	3	4	5	6	7
노드 번호	1	2	4	7	6	3	5

노드의 탈출 시각까지 저장을 진행해주면, 우리는 각 노드를 루트로 하는 서브트리를 하나의 구간[진입 시각, 탈출 시각]으로 나타낼 수 있다.

1번 노드 서브트리: [1, 7]
2번 노드 서브트리: [2, 5]
3번 노드 서브트리: [6, 7]
4번 노드 서브트리: [3, 3]
5번 노드 서브트리: [7, 7]
6번 노드 서브트리: [5, 5]
7번 노드 서브트리: [4, 5]

이러한 테크닉은 세그먼트 트리나 펜윅 트리를 이용하여 구간 갱신을 빠르게 할 때 빛이 난다.

// ETT(Euler Tour Technique)
void dfs(int x) {
	s[x] = ++cnt;
	for (int nx : v[x]) 
		dfs(nx);
	e[x] = cnt;
}

굉장히 단순하지만 강력한 테크닉이다.

BOJ 2820번: 자동차 공장

오일러 경로 테크닉을 공부하고 다들 이 문제를 풀어보길래... 한 번 풀어보았다.

segment tree와 lazy propagation를 같이 이용하여 해결해주었다.
소스코드