2021 부스트캠프 Day 25.
[Day 25] Graph
그래프 신경망이란 무엇일까? (기본)
변환식 정점 표현 학습과 귀납식 정점 표현 학습
-
이전의 정점 임베딩 방법들은 변환식(Transductive)방법이다.
-
변환식(Transductive) 방법은 학습의 결과로 정점의 임베딩 자체를 얻는다는 특성이 있다.
-
정점을 임베딩으로 변화시키는 함수, 즉 인코더를 얻는 귀납식(Inductive) 방법과 대조된다.
-
출력으로 임베딩 자체를 얻는 변환식 임베딩 방법은 여러 한계를 갖는다.
- 학습이 진행된 이후에 추가된 정점에 대해서는 임베딩을 얻을 수 없다.
- 모든 정점에 대한 임베딩을 미리 계산하여 저장해두어야 한다.
- 정점이 속성(Attribute) 정보를 가진 경우에 이를 활용할 수 없다.
-
출력으로 인코더를 얻는 귀납식 임베딩 방법은 여러 장점을 갖는다.
- 학습이 진행된 이후에 추가된 정점에 대해서도 임베딩을 얻을 수 있다.
- 모든 정점에 대한 임베딩을 미리 계산하여 저장해둘 필요가 없다.
- 정점이 속성(Attribute) 정보를 가진 경우에 이를 활용할 수 있다.

그래프 신경망 기본
그래프 신경망 구조
-
그래프와 정점의 속성 정보를 입력으로 받는다.
-
그래프의 인접 행렬을 A라고 하면, A는 |V| X |V|의 이진 행렬이다.
-
각 정점 u의 속성(Attribute) 벡터를 Xu라고 하면, 이는 m차원 벡터이고 m은 속성의 수를 의미한다.
-
정점의 속성의 예시:
- 온라인 소셜 네트워크에서 사용자의 지역, 성별, 연령, 프로필 사진 등
- 논문 인용 그래프에서 논문에 사용된 키워드에 대한 원-핫벡터 등
-
그래프 신경망은 이웃 정점들의 정보를 집계하는 과정을 반복하여 임베딩을 얻는다.
-
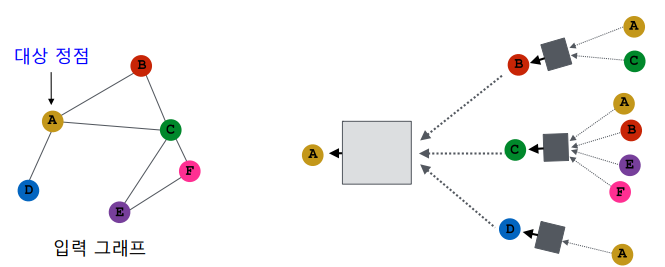
아래의 예시에서 대상 정점의 임베딩을 얻기 위해 이웃들 그리고 이웃의 이웃들의 정보를 집계한다.
-
각 집계 단계가 layer이고, 각 layer마다 임베딩을 얻게된다.
-
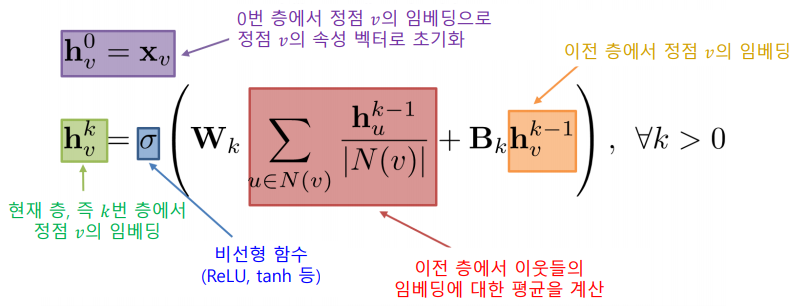
각 layer에서는 이웃들의 이전 층 임베딩을 집계하여 새로운 임베딩을 얻는다.
0번 층, 즉 입력 층의 임베딩으로는 정점의 속성 벡터를 사용한다.
-
대상 정점마다 집계되는 정보가 상이하다.
-
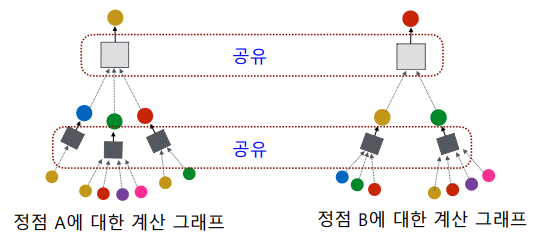
대상 정점 별 집계되는 구조를 계산 그래프(Computation Graph)라고 부른다.
-
서로 다른 대상 정점간에도 층 별 집계 함수는 공유한다.
-
입력의 크기가 가변적이여도 처리할수 있어야 한다. 어떻게 구성해야 할까?
-
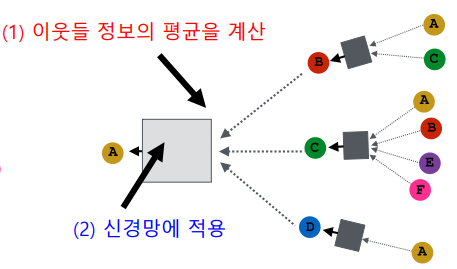
집계 함수는 두 단계를 거친다.
- 이웃들 정보의 평균을 계산
- 신경망에 적용
-
마지막 층에서의 정점 별 임베딩이 해당 정점의 출력 임베딩이다.

그래프 신경망 학습
-
그래프 신경망의 학습 변수는 층 별 신경망의 가중치이다.

-
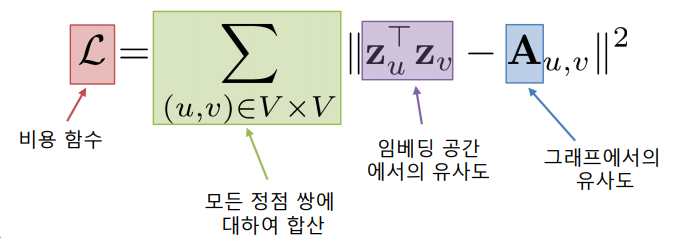
손실함수를 결정할 때, 정점간 거리를 "보존"하는 것을 목표로 할 수있다.
만약 인접성을 기반으로 유사도를 정의한다면, 손실함수는 다음과 같다.
-
Downstream Task의 손실함수를 이용한 End-to-End 학습도 가능하다.
-
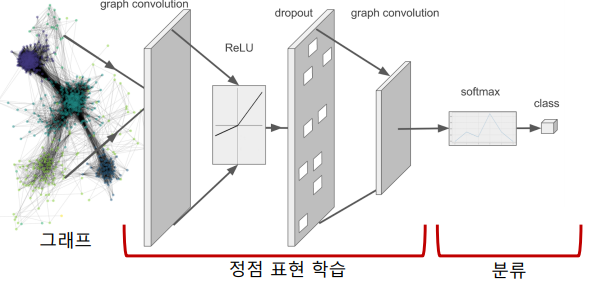
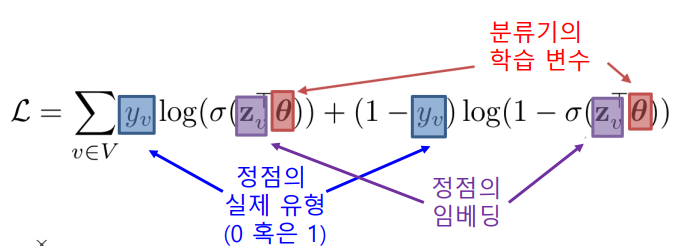
정점 분류가 목표인 경우를 생각하면,
- 그래프 신경망을 이용하여 정점의 임베딩을 얻고
- 이를 분류기(Classifier)의 입력으로 사용하여
- 각 정점의 유형을 분류
- 이 경우 분류기의 손실함수를 예를 들어 Cross Entropy를 손실함수로 사용할 수 있다.
-
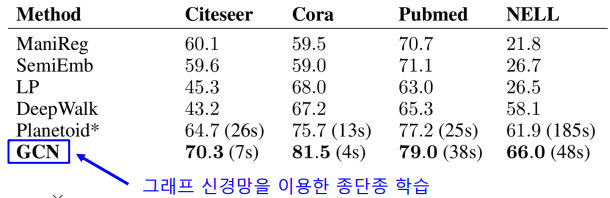
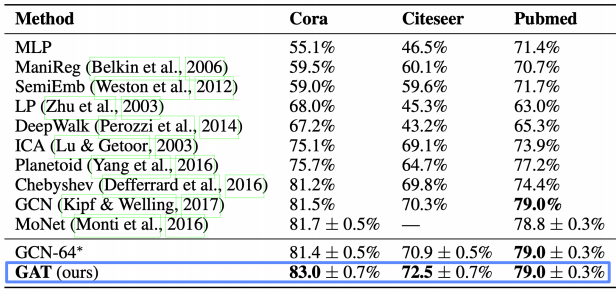
다양한 데이터에서의 정점 분류의 정확도
-
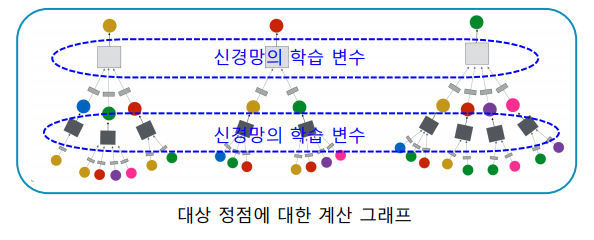
학습에 사용할 대상 정점을 결정하여 학습 데이터를 구성하고, 선택한 대상 정점들에 대한 계산 그래프를 구성한다.
-
마지막으로 오차 역전파(Backpropagation)을 통해 손실함수를 최소화한다.
그래프 신경망 활용
-
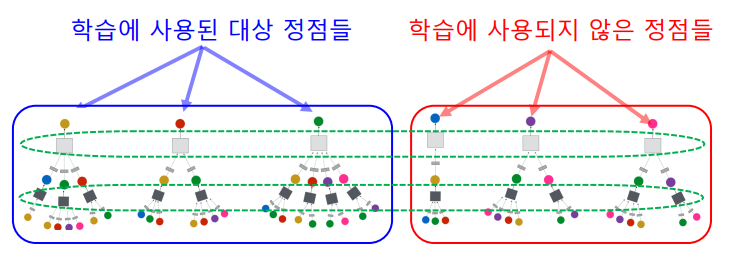
학습된 신경망을 적용하여, 학습에 사용되지 않은 정점의 임베딩을 얻을 수 있다.
-
학습된 그래프 신경망을, 새로운 그래프에 적용할 수도 있다.
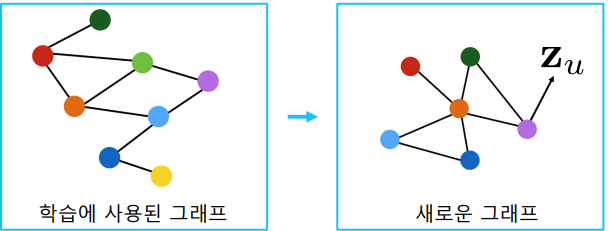
- 예를 들어, A종의 단백질 상호 작용 그래프에서 학습한 그래프 신경망을 B종의 단백질 상호작용 그래프에 적용할 수 있다.
그래프 신경망 변형
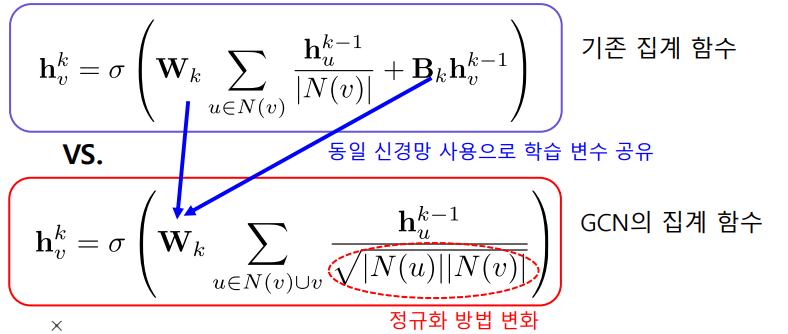
그래프 합성곱 신경망(Graph Convolutional Network, GCN)
- 집계함수는 아래와 같다. 기존의 집계함수와는 작은 차이지만 큰 성능의 향상으로 이어지기도 한다.
GraphSAGE
-
이웃들의 임베딩을 AGG 함수를 이용해 합친 후, 자신들의 임베딩과 연결(Concatenation)하는 점이 독특하다.

-
AGG 함수로는 평균, 풀링, LSTM 등이 사용될 수 있다.
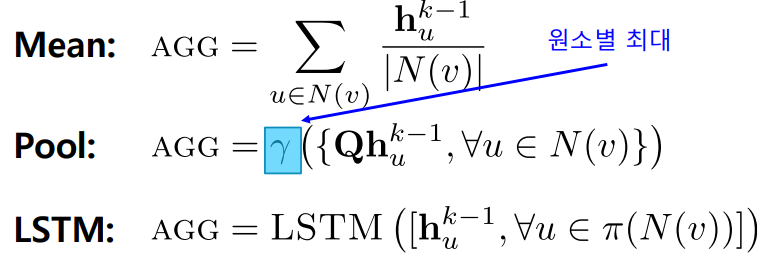
합성곱 신경망과의 비교
합성곱 신경망과 그래프 신경망의 유사성
-
합성곱 신경망과 그래프 신경망은 모두 이웃의 정보를 집계하는 과정을 반복한다.
-
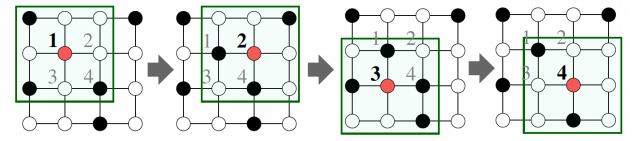
구체적으로, 합성곱 신경망은 이웃 픽셀의 정보를 집계하는 과정을 반복한다.
합성곱 신경망과 그래프 신경망의 차이
-
합성곱 신경망에서는 이웃의 수가 균일하지만, 그래프 신경망에서는 아니다.
-
그래프 신경망에서는 정점 별로 집계하는 이웃의 수가 다르다.

-
Q : 그래프의 인접 행렬에 합성곱 신경망을 적용하면 효과적일까?
-
그래프에는 합성곱 신경망이 아닌 그래프 신경망을 적용하여야 한다.
흔히 범하는 실수이다. -
합성곱 신경망이 주로 쓰이는 이미지에서는 인접 픽셀이 유용한 정보를 담고 있을 가능성이 높다.
-
하지만, 그래프의 인접 행렬에서의 인접 원소는 제한된 정보를 가진다.
특히나, 인접 행렬의 행과 열의 순서는 임의로 결정되는 경우가 많다.
-
그래프 신경망이란 무엇일까? (심화)
그래프 신경망에서의 어텐션
기본 그래프 신경망의 한계
-
기본 그래프 신경망에서는 이웃들의 정보를 동일한 가중치로 평균을 낸다.
-
그래프 합성곱 신경망에서는 단순히 연결성을 고려한 가중치로 평균을 낸다.
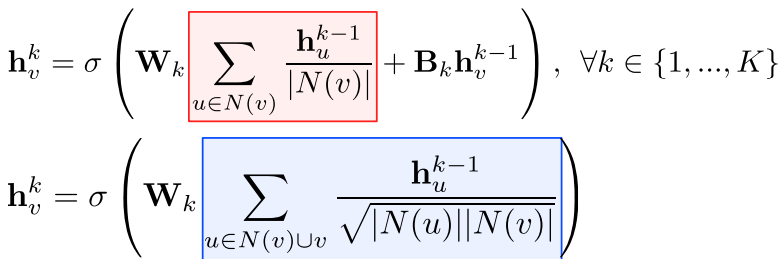
그래프 어텐션 신경망(Graph Attention Network, GAT)
-
가중치 자체도 학습한다.
-
실제 그래프에서는 이웃 별로 미치는 영향이 다를 수 있기 때문이다.
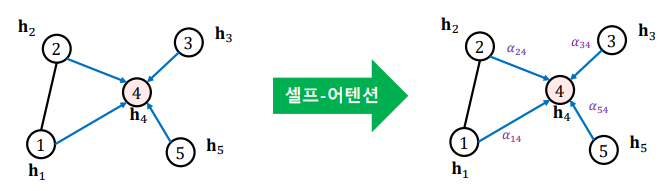
가중치를 학습하기 위해서 Self-Attention이 사용된다.
-
각 충에서 정점 i로부터 이웃 j로의 가중치 ij는 세 단계를 통해 계산한다.
- 해당 층의 정점 i의 임베딩 hi에 신경망 W를 곱해 새로운 임베딩을 얻는다.
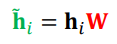
- 정점 i와 정점 j의 새로운 임베딩을 연결한 후, 어텐션 계수 를 내적한다.
어텐션 계수 는 모든 정점이 공유하는 학습 변수이다.
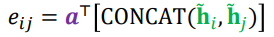
- softmax를 적용한다.
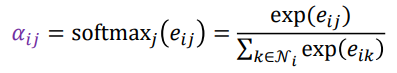
- 해당 층의 정점 i의 임베딩 hi에 신경망 W를 곱해 새로운 임베딩을 얻는다.
-
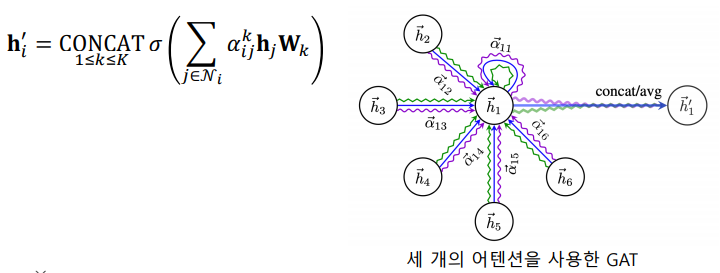
Multi-head Attention(여러개의 어텐션을 동시에 학습)한뒤, 결과를 연결하여 사용한다.
-
결과
그래프 표현 학습과 그래프 풀링
그래프 표현 학습
-
그래프 표현 학습, 혹은 그래프 임베딩이란 그래프 전체를 벡터의 형태로 표현하는 것
-
개별 정점을 벡터의 형태로 표현하는 정점 표현 학습과 구분된다.
그래프 임베딩은 벡터의 형태로 표현된 그래프 자체를 의미하기도 한다. -
그래프 임베딩은 그래프 분류 등에 활용된다.
그래프 형태로 표현된 화합물의 분자 구조로부터 특성을 예측하는 것이 한가지 예시이다.
그래프 풀링
-
정점 임베딩들로부터 그래프 임베딩을 얻는 과정
-
평균 등 단순한 방법보다 그래프의 구조를 고려한 방법을 사용할 경우 그래프 분류 등의 후속 과제에서 더 높은 성능을 얻는 것으로 알려져 있다.
-
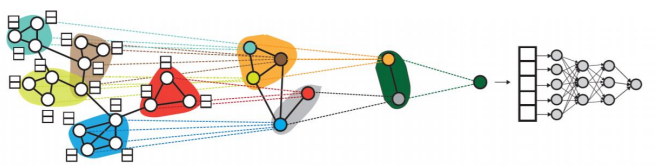
아래 그림의 미분가능한 풀링(Differentiable Pooling, DiffPool)은 군집 구조를 활용 임베딩을 계층적으로 집계한다.
지나친 획일화(Over-smoothing) 문제
지나친 획일화 문제
-
그래프 신경망의 층의 수가 증가하면서 정점의 임베딩이 서로 유사해지는 현상이 생기며 후속과제에서의 정화곧가 감소하는 현상이 발생한다.
-
지나친 획일화 문제는 작은 세상 효과와 관련이 있다.
-
적은 수의 층으로도 다수의 정점에 의해 영향을 받게 된다.

-
아래의 그림에서 보듯이 그래프의 신경망의 층이 2개 혹은 3개일 때 정확도가 가장 높다.
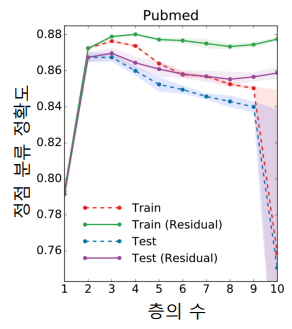
-
Residual을 넣는 것, 즉 이전 층의 임베딩을 한 번 더 더해주는 것 만으로는 효과가 제한적이다.
지나친 획일화 문제에 대한 대응
-
JK 네트워크(Jumping Knowledge Network)는 마지막 층의 임베딩 뿐 아니라, 모든 층의 임베딩을 함께 사용한다.
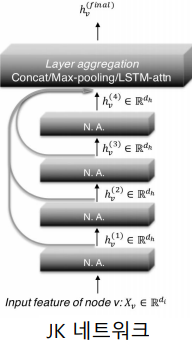
-
APPNP는 0번째 층을 제외하고는 신경망 없이 집계 함수를 단순화 하였다.
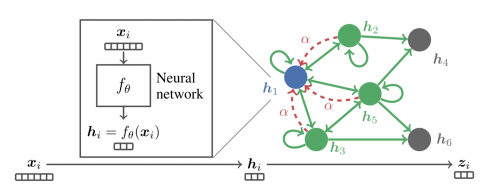
-
APPNP의 경우, 층의 수 증가에 따른 정확도 감소 효과가 없는 것을 확인하였다.
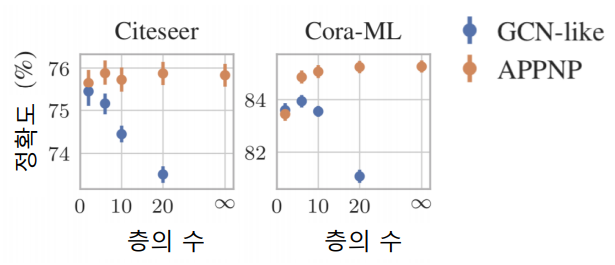
그래프 데이터 증강
그래프 데이터 증강
-
데이터 증강(Data Augmentation)은 다양한 기계학습에서의 효과적이다.
-
그래프에도 누락되거나 부정확한 간선이 있을 수 있고, 데이터 증강을 통해 보완할 수 있다.
-
임의 보행을 통해 정점간 유사도를 계산하고, 유사도가 높은 정점 간의 간선을 추가하는 방법이 제안되었다.
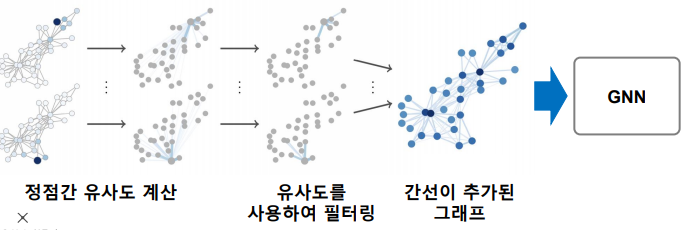
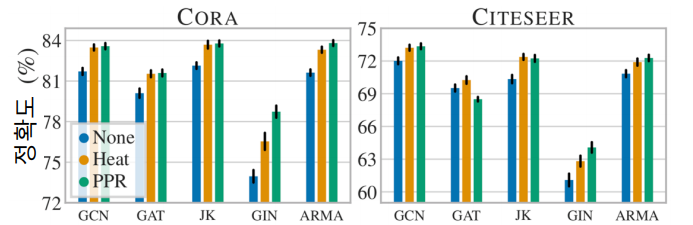
그래프 데이터 증강에 따른 효과
- 그래프 데이터 증강의 결과 정점 분류의 정확도가 개선 되는 것을 확인할수 있다.
Heat와 PPR은 유사도를 계산하는 방법이다.