[BOJ] 1로 만들기:1463 - python

오늘 풀어볼 문제는 1로 만들기이다.

문제

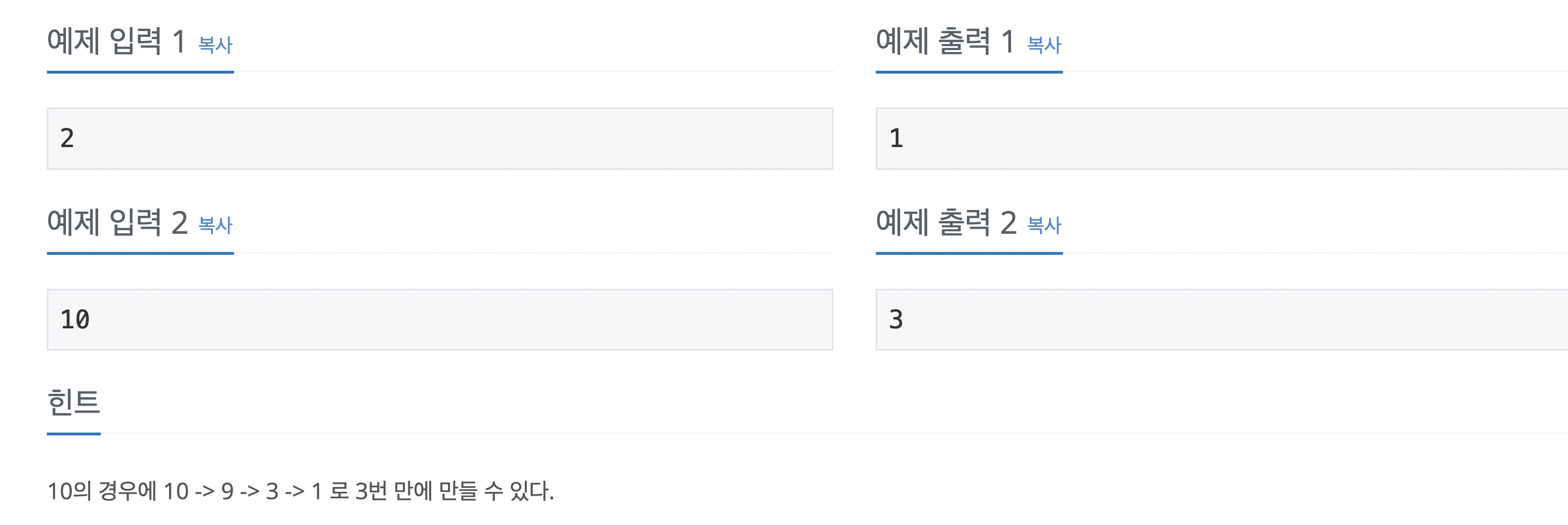
풀이 과정

이 문제를 보고 가장 처음 든 생각은 bfs가 아닐까 생각했다.
최단거리를 찾는 느낌이니까 말이다.

from collections import deque

n = int(input())

queue = deque([(n, 0)])

while queue:
    node, count = queue.popleft()

    if node == 1:
        print(count)
        break

    if node % 3 == 0:
        queue.append((node // 3, count + 1))

    elif node % 2 == 0:
        queue.append((node // 2, count + 1))

    queue.append((node - 1, count + 1))

  

그래서 이렇게 짜봤는데 결과는 59%에서 틀렸습니다 판정
그래도 어느정도 맞았다는 소리다!

문제를 해결하려고 좀 뻘짓을 하다가 그것도 안돼서 다시 곰곰이 생각해보니까 바보같은 짓을 발견 했다.
3으로 나눠지면서 동시에 2로도 나눠지는 수가 있는데 그걸 간과하고 elif로 처리해버렸다는 거다....

최종 코드

from collections import deque

n = int(input())

queue = deque([(n, 0)])

while queue:
    node, count = queue.popleft()

    if node == 1:
        print(count)
        break

    if node % 3 == 0:
        queue.append((node // 3, count + 1))

    if node % 2 == 0:
        queue.append((node // 2, count + 1))

    queue.append((node - 1, count + 1))

  

이렇게 if로 바꿔주니까 바로 통과했다

다른 사람의 풀이

보통 dp를 이용해 풀이를 하고 있었다.

n = int(input())
d = [0] * 1000001

for i in range(2, n+1):
    d[i] = d[i-1] + 1 # i라는 수의 1까지 최소 연산 횟수는 그 전의 수의 최소 연산 횟수 + 1회
    
    if i % 2 == 0: 
    	# i라는 수의 최소 연산 횟수는 그 전의 수의 최소 연산 횟수 + 1회,
        # i를 2로 나눈 수의 최소 연산 횟수 + 1회 중에 최솟값
        d[i] = min(d[i], d[i//2] + 1) 

    if i % 3 == 0:
        d[i] = min(d[i], d[i//3] + 1)

print(d[n])

이 방법이 내 방법보다 확실히 빠르다.

추가적으로 dp엗 대해 공부한 내용을 밑에 정리하고자 한다.

동적 계획법(dynamic programming)

복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다.
부분 문제 반복과 최적 부분 구조를 가지는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용한다.

부분 문제 반복 : 어떤 문제가 여러 개의 부분 문제(Subproblem)으로 쪼개질 수 있다는 뜻이다.
모든 문제를 부분 문제로 쪼갤 수 있고, 재귀 함수를 통해 해결 할 수 있다.

최적 부분 구조 : 작은 부분 문제의 최적의 답으로 큰 문제의 최적의 답을 구할 수 있다는 뜻이다.

접근 방법

1) Top-Down (위에서 아래로 접근)

• 큰 문제에서 부분 문제로 쪼개가며 문제를 풀어가는 방법이다.
• 재귀 호출을 이용하여 문제를 해결한다.
• 이전 계산값을 메모리에 저장하여 매번 다시 실행하지 않도록해서 실행 속도를 빠르게 하는 기술이다.
• 메모리를 더 사용해서 속도를 빠르게 한다.

def fibonacci_memoi(num):
    global memo
    if num >= 2 and len(memo) <= num:
        memo.append(fibonacci_memoi(num-1) + fibonacci_memoi(num-2))
    return memo[num]
memo = [0, 1]

2) Bottom-Up ( 아래에서 위로 접근)

• 부분 문제에서부터 문제를 풀어가며 점차 큰 문제를 풀어가는 방법이다.
• for문에서 배열을 이용하여 문제를 해결한다.

def fibonacci_dp(num):
    f = [0, 1]
    for i in range(2, num+1):
        f.append(f[i-1] + f[i-2])
    return f

활용방법

1. 변수 개수 만큼 메모를 위한 캐시 배열을 생성한다.
2. 문제를 부분 문제로 나누고, 점화식을 구하여 문제를 함수로 표현한다.
3. Top-Down의 경우 재귀 함수, Bottom-Up의 경우 for문을 활용하여 답을 도출한다.

동적 계획법은 모든 방법을 일일이 검토하여 최적의 해를 찾아내는 방식이기 때문에
항상 최적의 해를 검출하지만 시간이 오래 걸린다.

참고로 동적계획법이랑 비슷할 때 사용되는 그리디 알고리즘은 최적의 해가 아닐 수 있지만 시간이 적게 걸린다.
그래서 그리디 알고리즘은 내가 생각한 처음 최적의 방법이 끝까지 반례 없이 적용이 되는 경우에 사용하고
동적 계획법은 그게 아닐 경우에 사용한다.

언제 사용?

dp는 앞의 연산결과를 뒤에서 사용해야할 때, 가능성을 모두 두고 그 안에 최솟값을 찾을 때 사용한다.
그리디와 브루트포스의 중간 느낌이다.

알게된 점

• dp를 언제 쓰는 지, dp의 사용법

참고

https://jae04099.tistory.com/199
https://happy-time-daily-blog.tistory.com/47
https://dbstndi6316.tistory.com/35
https://velog.io/@khjcode/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-DP-%EB%AC%B8%EC%A0%9C-%ED%92%80%EA%B8%B0-%ED%8C%8C%EC%9D%B4%EC%8D%AC
https://seongonion.tistory.com/40