[BOJ] 소수&팰린드롬 - python

이번에 풀어볼 문제는 소수&펠린드롬이다.

그냥 while문 돌리면서 n을 1씩 증가시키면서 n이 펠린드롬인지 판단하고 그 후에 소수인지 판단해서 둘다 만족하면 print하고 break하면 되겠다 해서 그렇게 짜 보았다.

n = int(input())


def is_prime(n):
    if n < 2:
        return False

    for i in range(2, n):
        if n % i == 0:
            return False
    return True

def is_pelindrome(n):
    splited_numbers = list(str(n))
    return splited_numbers == list(reversed(splited_numbers))

while True:
	if is_pelindrome(n):
        if is_prime(n):
            print(n)
            break

    n += 1

사실 이거 시간초과 날 줄 알고 시간초과나면 에라토스테네스의 체를 이용해서 소수를 구해놓는 걸로 바꿔야 겠다 했는데 그냥 통과가 됐다.

그리고 참고로 펠린드롬 수를 먼저 판별한 후에 소수를 판별하기 때문에 시간초과가 안난거고, 반대로 하면 시간초과가 난다.

그래서 그냥 에라토스테네스의 체를 이용한 방법도 짜보았다.

import sys

input = sys.stdin.readline

n = int(input())

MAX = 2000000
sieves = [True] * MAX
sieves[1] = False

for i in range(2, MAX):
    if sieves[i]:
        for j in range(i * 2, MAX, i):
            if sieves[j]:
                sieves[j] = False

# def is_prime(n):
#     if n < 2:
#         return False

#     for i in range(2, n):
#         if n % i == 0:
#             return False
#     return True


def is_pelindrome(n):
    splited_numbers = list(str(n))
    return splited_numbers == list(reversed(splited_numbers))


def is_prime(n):
    return sieves[n]


while True:
    if is_prime(n):
        if is_pelindrome(n):
            print(n)
            break

    n += 1

시간 단축이 됐다.

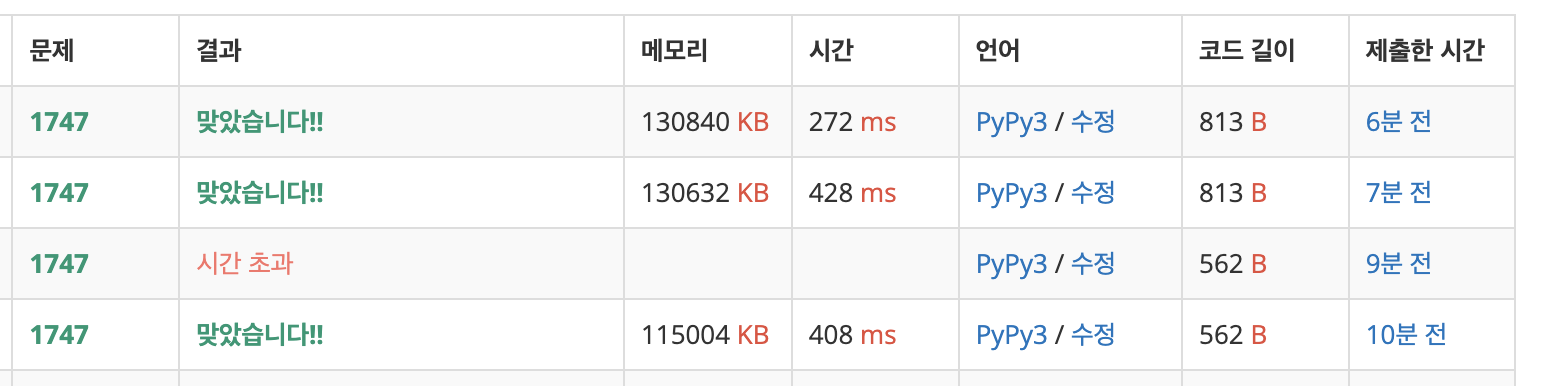
한번 실험을 해봤는데 408ms 짜리는 에라토스테네스 체를 이용하지 않았을 때, 시간 초과는 에라토스테네스 체를 이용하지 않았는데 소수 먼저 판별한 다음에 팰린드롬 수를 판별했을 때, 428ms 짜리는 에라토스테네스 체를 이용했는데 펠린드롬 먼저 판별하고 소수를 판별했을 때 그리고 272ms짜리는 에라토스테네스 체를 이용했는데 소수를 먼저 판별하고 펠린드롬 수를 판별했을 때다.

에라토스테네스 체 + 소수 판별 이후 펠린드롬 수 판별
이 조합이 가장 시간이 적게 걸리는 걸 확인할 수 있었다. 아무래도 소수는 한번 계산해놓으면 그 이후로는 계산을 안해도 되니까 이런 결과가 나온 것 같다.