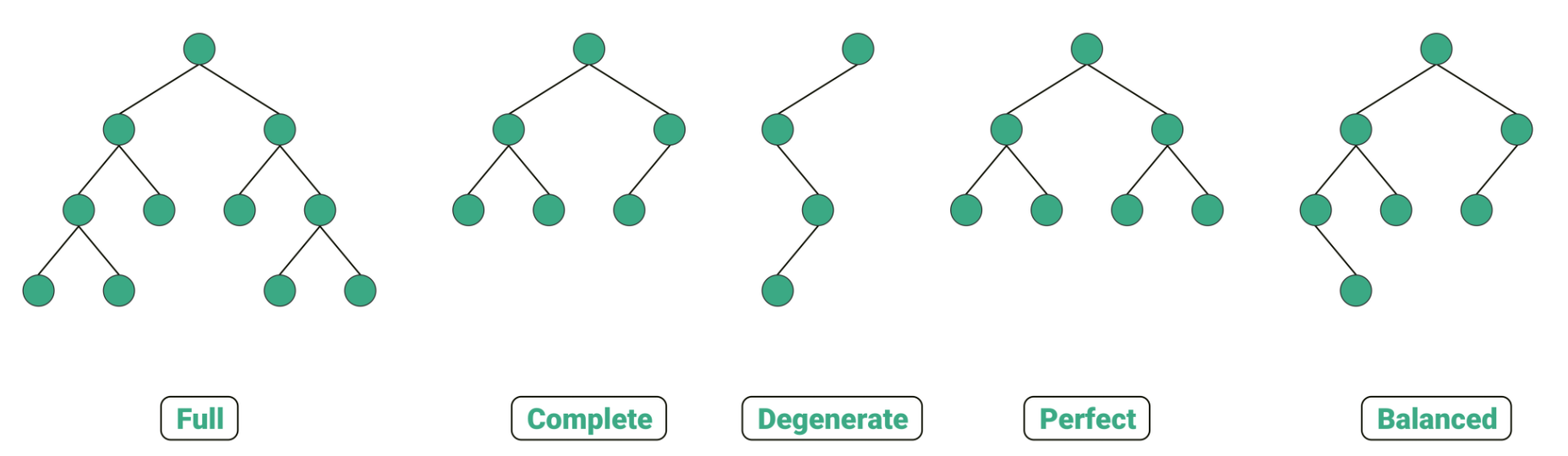
면접 때 이진트리 관련해서 질문을 받았었다.
바이너리 트리에 대해서 배우기는 했지만 종류 같은 것들이 대강은 기억나지만 디테일 하게 기억이 나지 않았다.
그래서 풀 바이너리 트리 물어보는데 컴플릿 바이너리 트리 개념 말하고(그것도 제대로 답 못함) 난리 났다.
면접 끝나고 궁금해서 찾아봤는데 이진 트리 종류가 많아서 헷갈려서 이 참에 정리 하고자 한다.
1. 이진트리 (binary tree)
모든 노드들이 둘 이하(0,1,2 개)의 자식을 가진 트리이다.
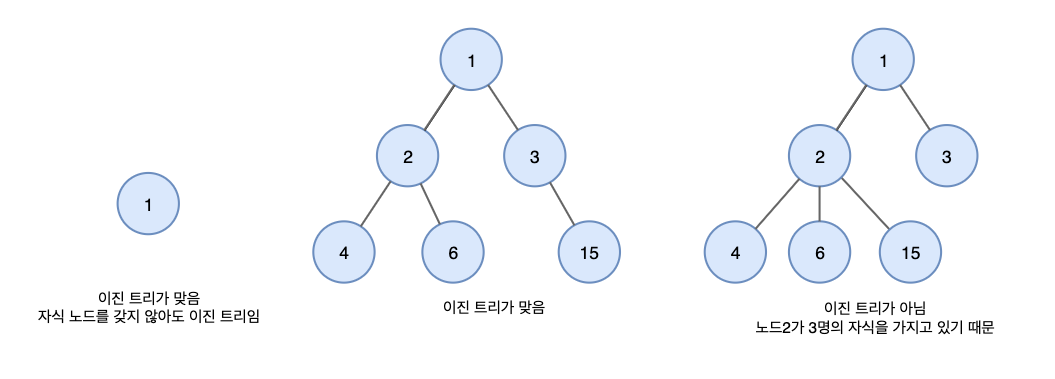
2. 이진 탐색 트리(Binary Search Tree, BST)
왼쪽 자식은 부모보다 작고 오른쪽 자식은 부모보다 큰 이진 트리이다.
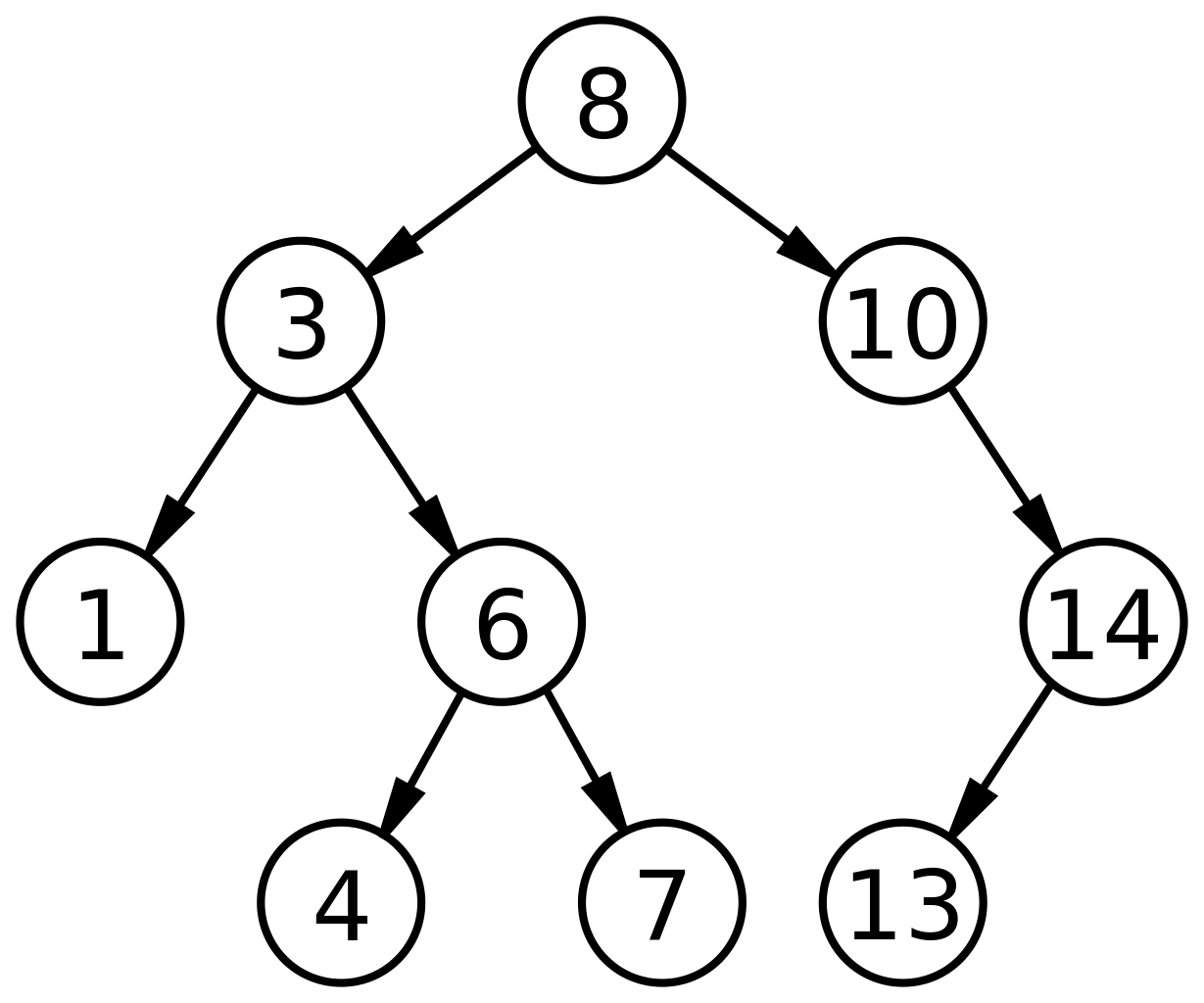
조건
1) 부모 노드의 왼쪽 노드는 부모 노드보다 작아야 한다.
2) 부모 노드의 오른쪽 노드는 부모 노드보다 커야 한다.
BST는 삽입, 삭제, 탐색과정에서 모두 트리의 높이만큼 탐색하기 때문에 O(logN)의 시간 복잡도를 가진다.
문제는 트리가 편향트리가 되어버렸을 때 결국 배열과 다름 없어지고 시간 복잡도는 O(N)이 된다.
중위순회(inorder traversal)를 하면, 오름차순으로 정렬된 순서로 Key값을 얻을 수 있다.
참고로 순회 종류는 아래와 같다.
⊙ 전위 순회(preorder traverse) : 뿌리(root)를 먼저 방문
- 뿌리 -> 왼쪽 자식 -> 오른쪽 자식
( 8 -> 1 -> 3 -> 6 -> 4 -> 7 ....)
⊙ 중위 순회(inorder traverse) : 왼쪽 하위 트리를 방문 후 뿌리(root)를 방문
- 왼쪽자식 -> 뿌리 -> 오른쪽 자식
( 1 -> 3 -> 4 -> 6 -> 7 -> 8 -> ...)
⊙ 후위 순회(postorder traverse) : 하위 트리 모두 방문 후 뿌리(root)를 방문
- 왼쪽자식-> 오른쪽 자식 -> 뿌리
(1 -> 4 -> 7 -> 6 -> 3 -> 13 -> ..)
3. 정 이진트리(full binary tree)란?
모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리이다.
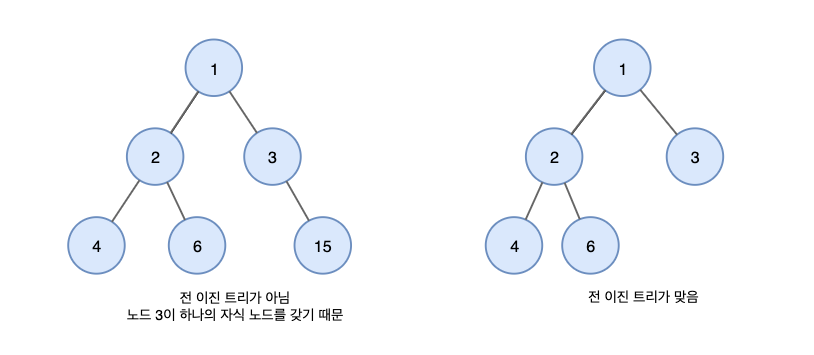
4. 완전 이진트리(complete binary tree)란?
마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리이다.
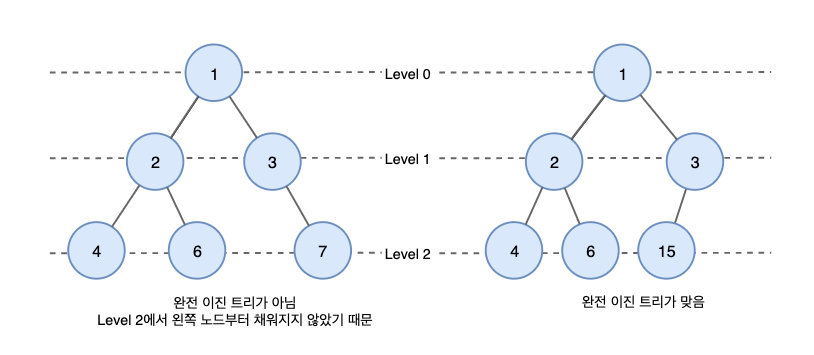
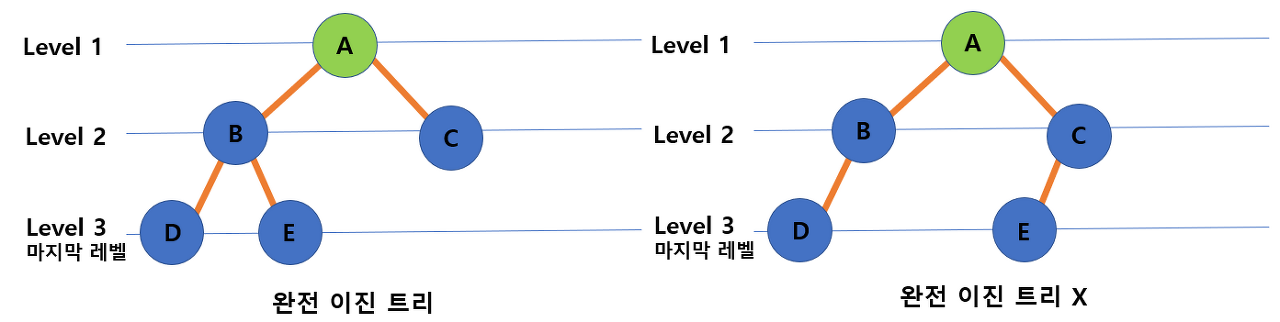
마지막 레벨은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
완전 이진 트리의 개념은 힙(heap)과 관련이 있다.
5. 완전 이진 탐색 트리(Complete binary search tree)란?
완전 이진 트리의 성질을 가지는 이진 탐색 트리이다.
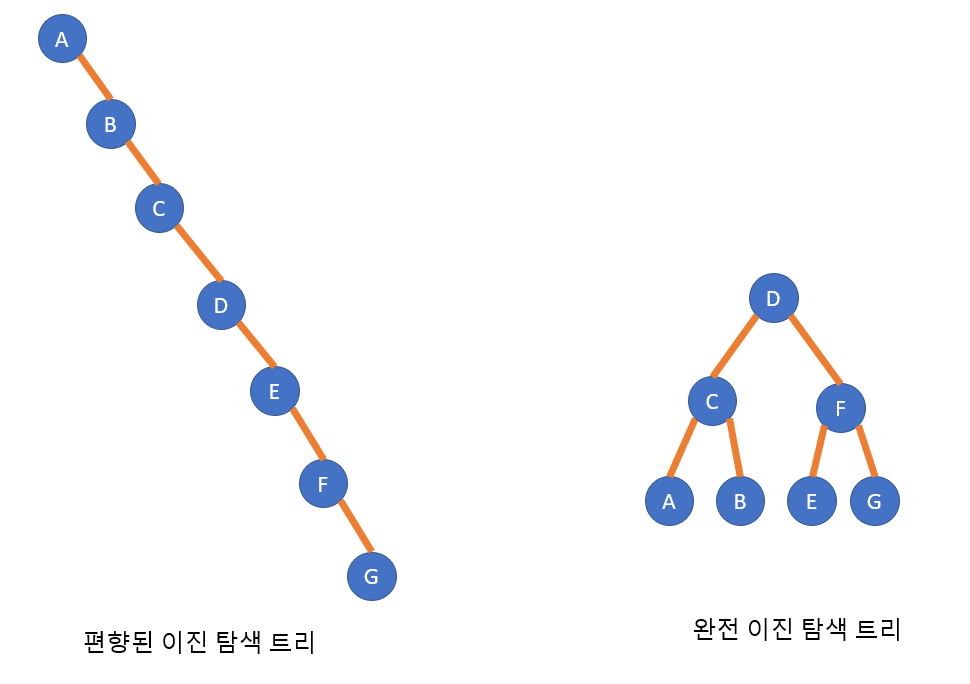
편향된 이진 탐색 트리와 다르게 항상 O(log n)의 검색 속도를 보장한다.
하지만 트리에 자료가 삽입될 때 마다 완전 이진 탐색 트리의 형태를 유지하기 위해
트리의 모양을 바꾸어야 하기 때문에 삽입 시 시간이 많이 소요된다.
따라서 삽입이 적고 탐색이 많은 경우에 유리하며
삽입하는 빈도수가 높아지면 효율성이 떨어지고 이를 해결한 것이 AVL트리이다.
6. 포화 이진 트리 (Perfect Binary Tree)
정 이진 트리이면서 완전 이진 트리인 경우이다.
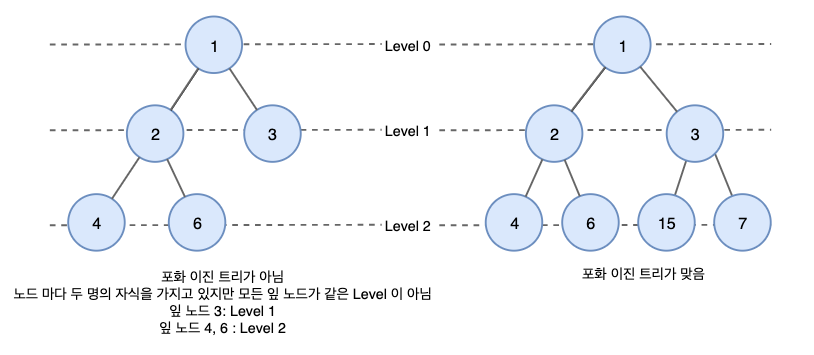
모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리이다.
즉, 모든 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는다.
7. 편향 이진트리(skewed binary tree)
같은 높이의 이진 트리 중에서 최소 개수의 노드 개수를 가지면서
왼쪽 혹은 오른쪽 서브트리만을 가지는 이진트리이다.
즉 모든 노드가 왼쪽에 있거나 반대로 오른쪽에 있는 트리이다.
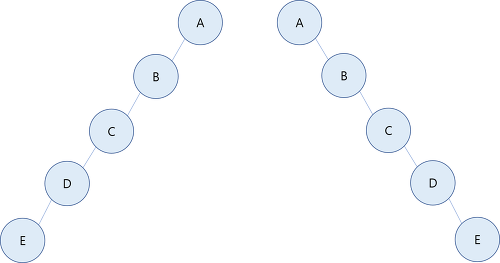
각 부모 노드가 오직 한 개의 연관 자식 노드를 갖는 트리이다.
사향 이진 트리(Degenerate (or Pathological) Tree) 라고도 부른다.
Linked List 성능과 동일하다.
8. 균형 이진 트리 (Balanced Binary Tree)
높이 균형이 맞춰진 이진트리이다.
왼쪽과 오른쪽 트리의 높이 차이가 모두 1만큼 나는 트리이다.
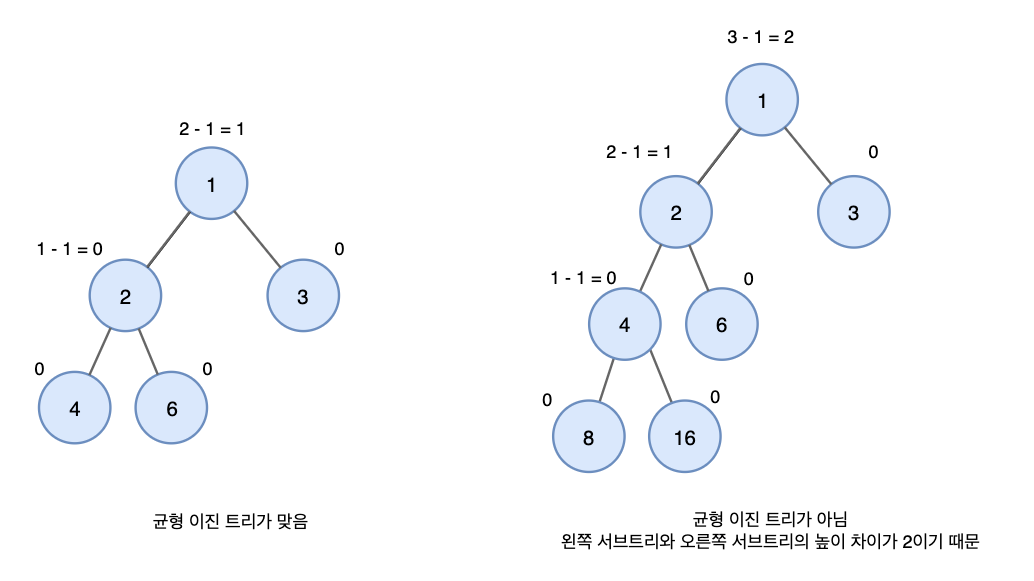
예로는 AVL(높이 균형 이진 탐색 트리) 과 Red-Black 트리가 있다.
9. 높이 균형 이진 탐색 트리 (Adelson-Velsky and Landis, AVL 트리)
스스로 균형을 잡는 이진 탐색 트리이다.
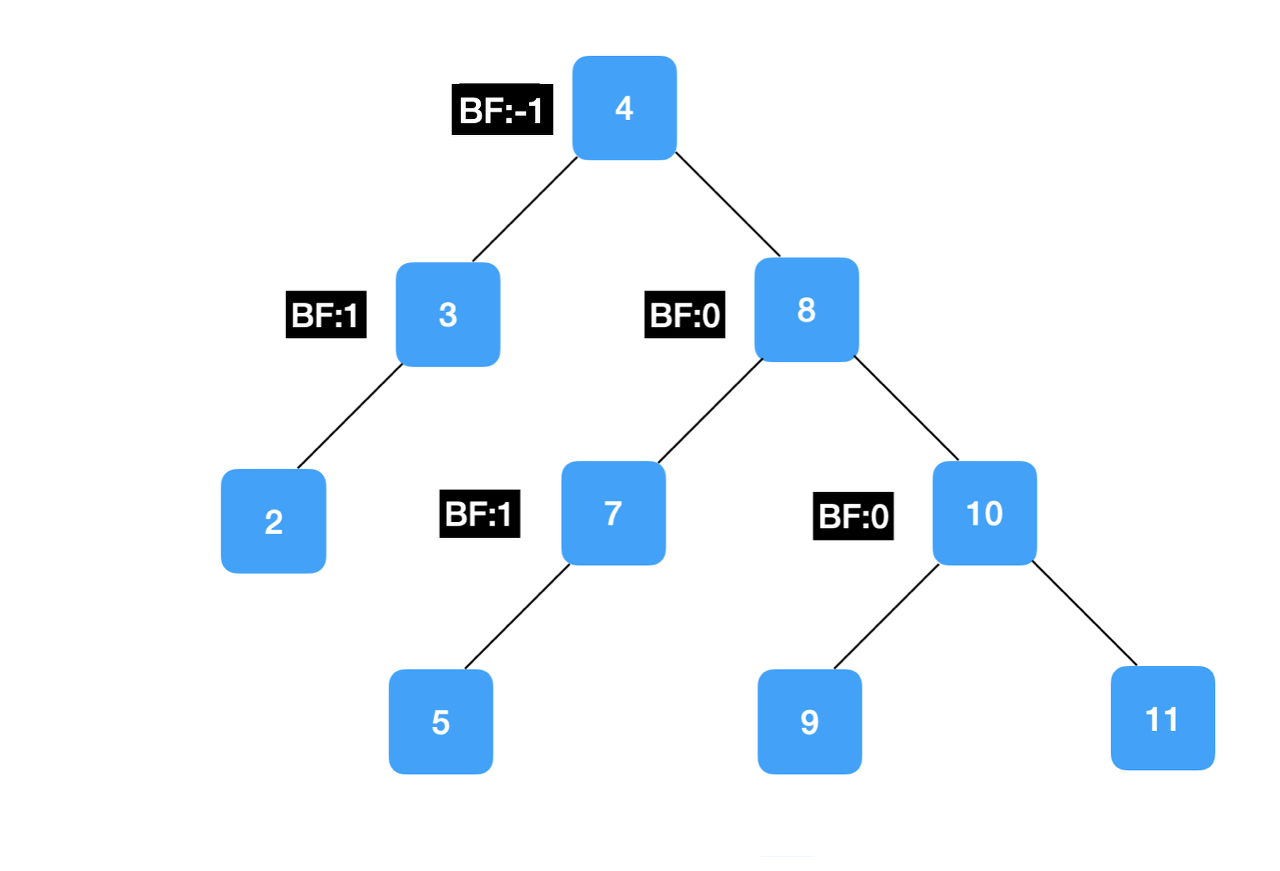
균형을 잡을 때 핵심되는 것은 바로 Balance Factor라는 것인데
Balance Factor는 왼쪽과 오른쪽의 자식의 높이 차이를 뜻한다.
이 때 균형이 잡혔다는 것은 BF가 최대 1까지 차이나는 것, 즉 -1부터 1까지일 때를 의미한다.
이진탐색 트리는 삽입, 삭제, 탐색 모두 평균은 O(logN)이지만 최악은 O(N)인데,
AVL트리는 삽입, 삭제, 탐색 모두 평균이든 최악의 경우든 O(logN)이다.
AVL 트리에서 삽입, 삭제 연산을 수행할 때 트리의 균형을 유지하기 위해
LL-회전, RR-회전, LR-회전, RL-회전연산이 사용된다.
회전에 대하 자세한 설명은 이 블로그에 잘 설명돼 있다.
Red-Black 트리
자가 균형 이진 탐색 트리이다.

조건
1. 모든 노드는 빨간색 혹은 검은색이다.
2. 루트 노드는 검은색이다.
3. 모든 리프 노드(NIL)들은 검은색이다. (NIL : null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드)
4. 빨간색 노드의 자식은 검은색이다.
== No Double Red(빨간색 노드가 연속으로 나올 수 없다)
5. 모든 리프 노드에서 Black Depth는 같다.
== 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.
이진 탐색 트리와 달리 최악의 경우에도 O(log n)의 시간복잡도로 삽입, 삭제, 검색을 할 수 있기 때문에 사용한다.
AVL 트리는 균형을 엄격하게 유지하는데, red-black tree는 색상이 추가되어 여유롭게
균형을 유지하기 때문에 AVL 트리에 비하여 삽입, 삭제가 빠르다.
만드는 방법은 이 블로그에 자세히 설명돼 있다.
왜 RB tree가 AVL tree보다 많이 쓰일까?
두 트리 모두 삽입, 삭제, 검색시 O(logN) 의 시간이 소요되는건 똑같다.
하지만 AVL tree는 트리의 밸런스가 좀 더 엄격하게 유지되기 때문에 탐색에 유리하고
RB tree 는 밸런싱을 느슨하게 하기 때문에 AVL tree에 비해 탐색엔 불리하지만 삽입, 삭제에 유리하다.
참고 자료
- https://kingpodo.tistory.com/27
- https://yoongrammer.tistory.com/69
- https://kangworld.tistory.com/51
- https://limecoding.tistory.com/117
- https://fomaios.tistory.com/entry/Data-Structure-%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-%ED%8A%B8%EB%A6%ACBinary-Search-Tree%EB%9E%80
- https://fomaios.tistory.com/entry/Data-Structure-AVLAdelson-Velsky-and-Landis-%ED%8A%B8%EB%A6%AC%EB%9E%80
- https://code-lab1.tistory.com/62

정성스런 글 잘 봤습니다 :)