CS 스터디를 시작했는데 스터디하면서 공부한 배열과 링크드 리스트에 대해서 정리하고자 한다.
배열
입력된 데이터들이 메모리 공간에서 연속적으로 저장되어 있는 자료구조이다.

크기가 고정돼 있어서 크기 수정을 못하고 배열 크기 이상의 데이터를 저장할 수 없다.
그러니까 새로 큰 배열을 만들어서 복사하든지 해야한다.
장점
- 인덱스만 알고 있으면 탐색이 매우 빠르다.
단점
-
데이터를 처음이나 중간에 삽입/삭제할 때 시간이 오래 걸린다.
(그 이후의 데이터들을 뒤로 한 칸 씩 shift해야되기 때문에) -
크기가 고정적이다.
시간복잡도
- 인덱스로 탐색: O(1)
- 순차적으로 탐색: O(n)
- 배열의 처음 또는 중간에 삽입 및 삭제: O(n) (삽입 지점 이후의 데이터를 옮겨야 하기 때문)
- 배열의 끝에 삽입 및 삭제: O(1)
연결 리스트
여러 개의 노드들이 순차적으로 연결된 형태를 갖는 자료구조이다.

첫번째 노드를 헤드(Head), 마지막 노드를 테일(Tail) 이라고 한다.
각 노드는 데이터와 다음 노드를 가리키는 포인터로 이루어져있다.
배열과는 다르게 메모리를 연속적으로 사용하지 않는다.
그렇기 때문에 크기 제한이 없어서 데이터 추가, 삭제가 자유롭다.
왜냐하면 메모리가 서로 떨어져 있어도 선형구조로 데이터를 저장할 수 있기 때문에
배열과는 다르게 순차적으로 접근해야 하는 면에서 불리할 수도 있으나,
노드가 연결된 구조이기 때문에 삽입, 삭제에 용이하다.
요소를 삽입, 삭제할 때마다 메모리의 할당,해제가 일어난다.
이 작업은 시스템 콜(System Call)을 사용하기 때문에 시간 소요가 꽤 걸린다.
장점
- 데이터를 차례대로 순회하면서 연산하기 좋다.
- 순회 도중에 새로운 데이터의 삽입,삭제에 용이하다. ( 포인터만 바꿔주면 되니까 )
- 배열과는 달리 데이터의 개수를 모르는 경우에도 별도의 비용없이 추가할 수 있다.
시간복잡도
탐색: O(n)
삽입 및 삭제: 삽입과 삭제 자체는 O(1) 이다.
연결리스트의 처음에 삽입 및 삭제: O(1)
연결리스트의 중간에 삽입 및 삭제: O(n) (탐색을 해야해서)
연결리스트의 끝에 삽입 및 삭제:
끝을 가리키는 별도의 포인터를 갖는 경우: O(1)
끝을 가리키는 별도의 포인터를 갖지 않는 경우: O(n) (탐색을 해야해서)
즉, 탐색은 O(n)이 걸리고
처음과 끝에 삽입이나 삭제를 할 경우 O(1)
중간에 삽입이나 삭제를 할 경우 탐색이 필요하기 때문에 O(n) 이다.
배열 VS 연결 리스트
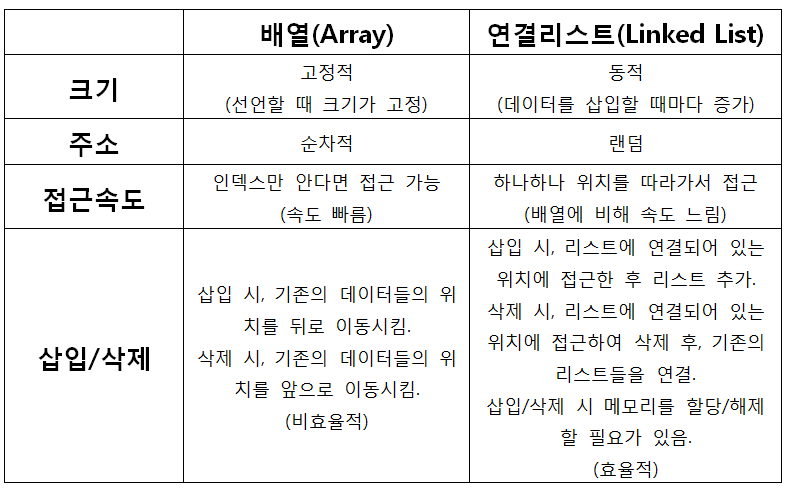
데이터 접근이 자주 일어날 때 -> 배열
데이터 수정이 자주 일어날 때 -> 링크드 리스트
이중 연결 리스트
전/후로 탐색이 가능한 구조이다.
즉, 단순 연결 리스트의 노드는 데이터와 다음 노드의 주소를 저장한다면
이중 연결 리스트의 노드는 데이터, 이전 노드의 주소와 다음 노드의 주소를 저장하게 된다.
장점
- 단순 연결 리스트에서는 최악의 경우 n번의 탐색을 해야하지만
이중 연결 리스트에서는 얻고자 하는 데이터의 위치가 tail에 가깝다면
tail에서부터 역방향으로 탐색이 가능하기 때문에 탐색 시간을 줄일 수 있다.
단점
- 이전 노드의 주소도 함께 저장해야 하기 때문에 단순 연결 리스트 보다 메모리를 더 많이 잡아 먹는다.
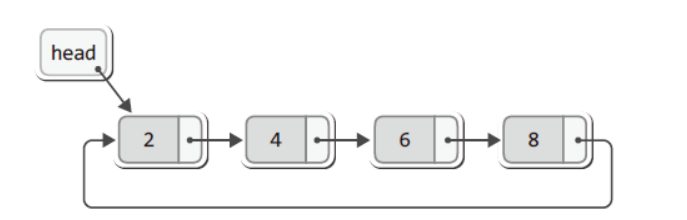
원형 연결 리스트 (Circular Linked List)

마지막 노드가 null을 가리키는 게 아닌 처음 노드를 가리키는 구조이다.
즉, head에서부터 순회를 반복적으로 진행하다보면 다시 처음으로 돌아오는 구조이다.
이중 연결 리스트도 마지막 노드가 처음 노드를 가리키는 구조가 되면, 이를 이중 원형 연결 리스트라고 한다.
head와 tail 포인터를 따로 두지 않고 하나의 포인터만 가지고 머리 또는 꼬리에 노드를 추가할 수 있다.
노드를 추가할 때 꼬리에 추가하려하면 tail에 추가하고 머리에 추가하고 싶을 땐 tail->next에 추가하면 된다.
장점
- head와 tail 포인터를 따로 두지 않고 하나의 포인터만 가지고 머리 또는 꼬리에 노드를 추가할 수 있다.
단점
- 구현하는 데 있어서 단순 연결 리스트 보다 복잡해진다.
스터디에서 새로 알게 된 점
이진 트리를 구현할 때 배열로 구현하면 메모리 낭비가 너무 크기 때문에 링크드 리스트로 구현한다고 한다.
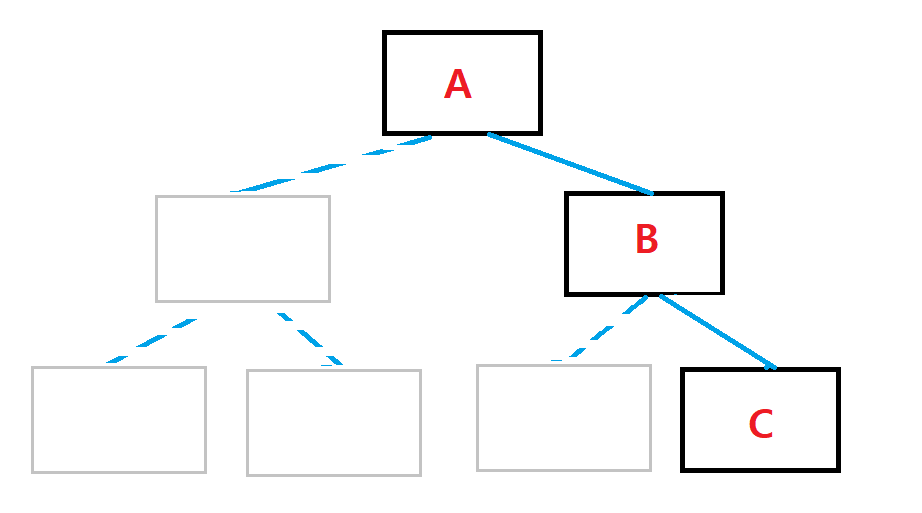
배열로 구현하면 이렇게 단 3개의 데이터를 저장하는데 7개의 공간이 필요하다.
이진트리가 완전히 다 차 있는(포화 이진트리) 게 아니라면 메모리 낭비가 심하다.
