[백준 BOJ] 재귀 문자열:23564 - python

이번에 풀어볼 문제는 재귀 문자열이다.

풀이과정

이 문제를 풀려고 했는데 나는 문제를 어떻게 풀 지 아이디어가 생각나지 않았다.
그래서 블로그를 좀 참고했다.

이 문제를 풀려고 시도한 사람 자체가 적어서 참고할 블로그가 없어서 난감했는데
감사하게도 C언어로 이 문제를 풀고 매우 잘 정리해주신 분이 있었다.

해당 블로그를 보고 얻은 아이디어는 아래와 같다.

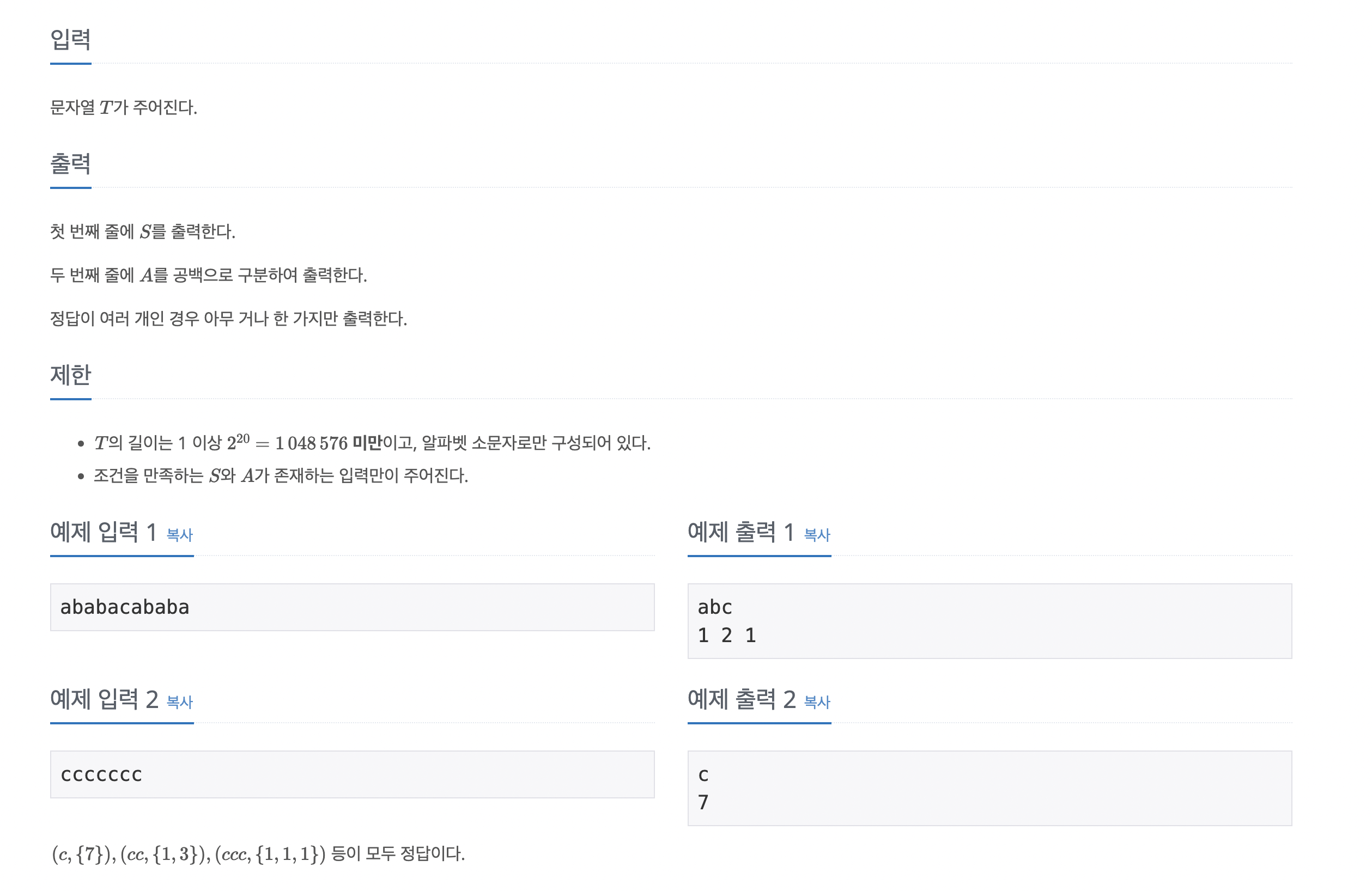
T를 ababacababa라고 하면 각 패턴을 구하는 로직은 아래와 같이 설명할 수 있다.

첫번 째 패턴 (a)
s1은 제일 처음 나온 알파벳(a)
a1은 제일 처음 나온 알파벳이 반복된 횟수(1)

두번 째 패턴 (ababa)
s2는 s1이 a1만큼 반복된 이후의 알파벳(b)
a2는 첫번 째 패턴과 s2를 합친 서브패턴(ab)이 연속으로 몇번 나왔는 지 계산한 횟수(2)

세번 째 패턴 (ababacababa)
s3는 두번째 패턴 후의 알파벳(c)
a2는 두번 째 패턴과 s3를 합친 서브패턴(ababac)이 연속으로 몇번 나왔는 지 계산한 횟수(1)
.
.
.
(계속 반복)

이 로직대로 파이썬 코드를 짜보았다.

T = input()
T_length = len(T)

s = [""]
a = [0]


def recursion(n, previous_pattern_length):
    if n == 0:  # 첫 번 째 패턴을 찾을 경우
        s[0] = T[0]

        for i in range(0, T_length):  # 첫번 째 알파벳이 반복된 횟수 계산
            if s[0] != T[i]:
                break

            a[0] += 1

        recursion(n + 1, a[0])

    else:
        if previous_pattern_length == T_length:
            return

        a.append(0)
        s.append("")

        # sn 은 이전 패턴 바로 뒤의 알파벳
        s[n] = T[previous_pattern_length]

        # 서브패턴 = 처음 ~ 이전패턴 바로 뒤의 알파벳
        sub_pattern = T[: previous_pattern_length + 1]
        sub_pattern_length = len(sub_pattern)

        # 서브 패턴이 연속적으로 몇번 나타나는 지 계산 해서 an 구함
        for i in range(0, T_length, sub_pattern_length):
            # 서브 패턴이 더이상 반복되지 않으면 break
            if sub_pattern != T[i : i + sub_pattern_length]:
                break

            a[n] += 1  # 서브 패턴이 반복됐으면 an 1증가

        # 현재 패턴 길이는 이전 패턴 길이 * (an + 1) + an
        # ex) ababa는 1*(2+1) + 2 = 5
        pattern_length = previous_pattern_length * (a[n] + 1) + a[n]

        recursion(n + 1, pattern_length)


recursion(0, 0)

print("".join(s))
print(" ".join(map(str, a)))

결과는 통과