오늘 풀어볼 문제는 전화번호 목록이다.
문제
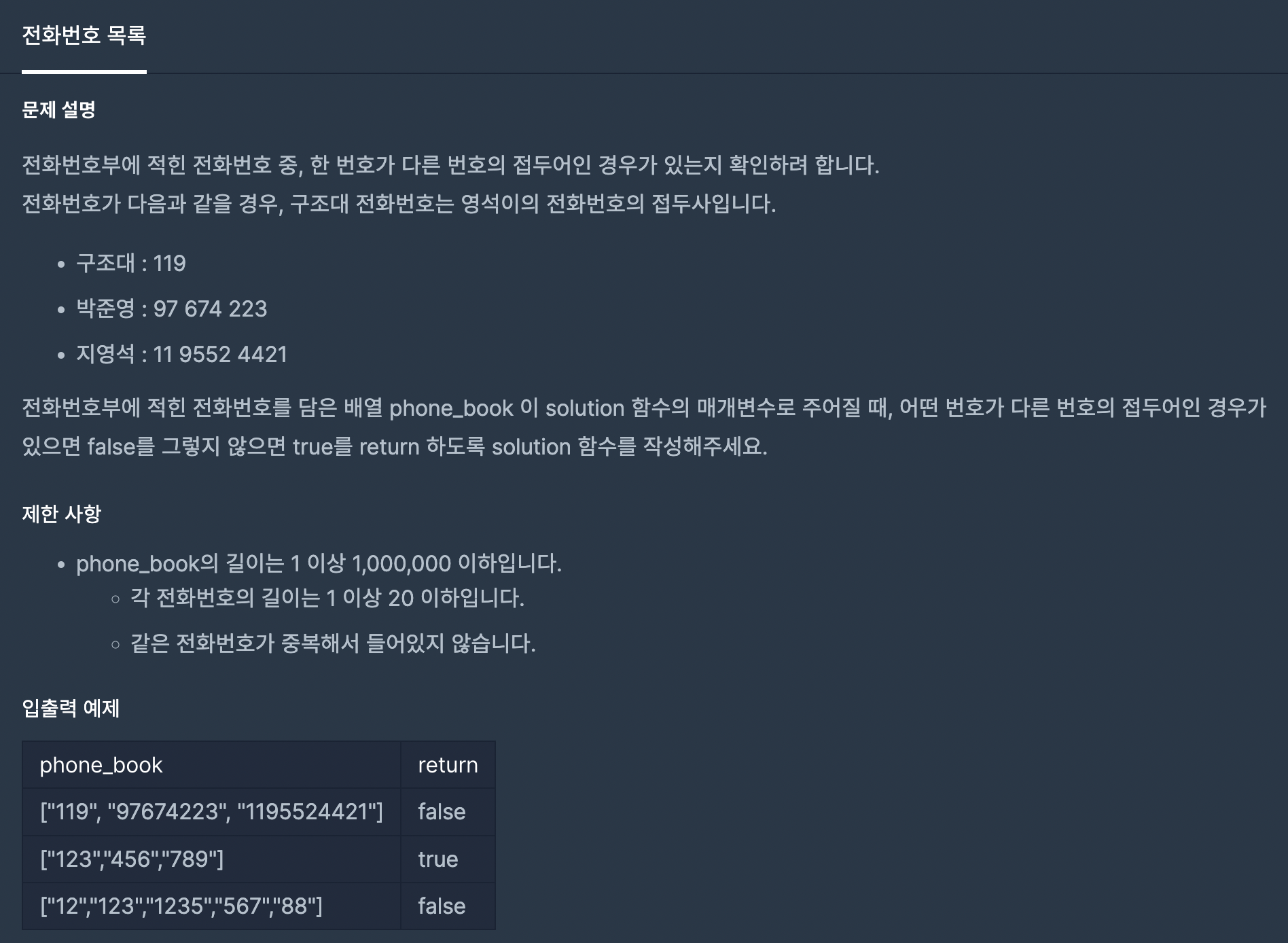
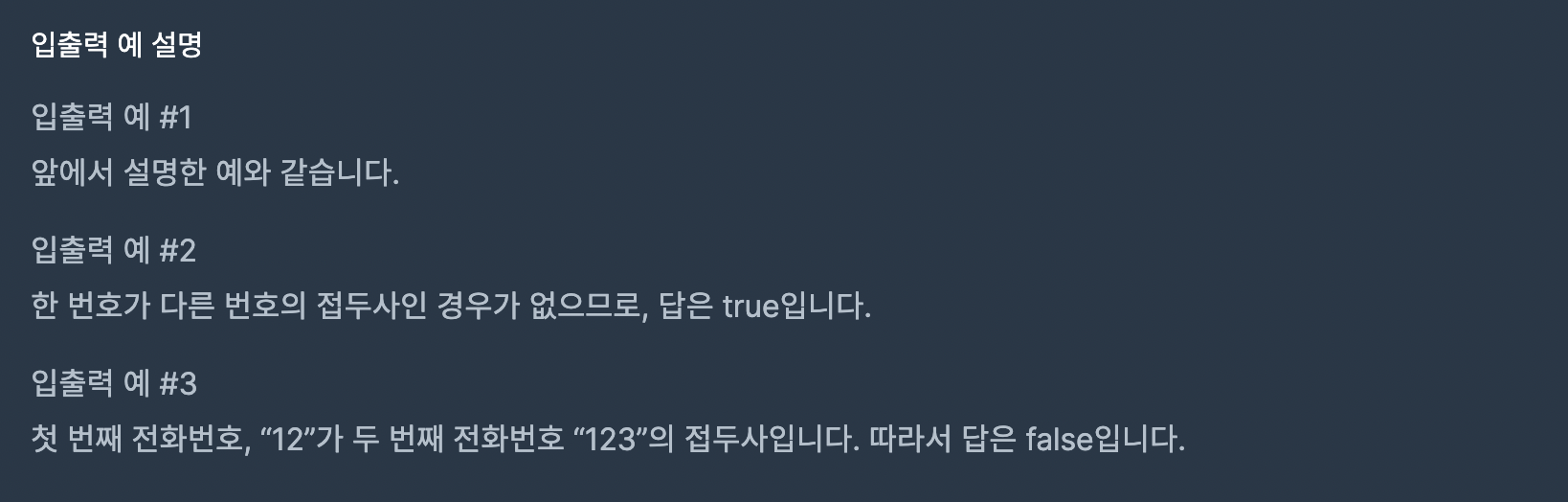
풀이 과정
처음 든 생각은 모든 전화번호 조합들을 startswith 함수를 써서 판단하면 되지 않을까였다.
동시에 든 생각은 물론 되겠지만 효율성 검사에서는 무조건 탈락이겠지..
그렇지만 그거 외에는 다른 생각이 나지 않았기 때문에 일단 그냥 구현은 해봤다.
def solution(phone_book):
answer = True
length = len(phone_book)
for i in range(length-1):
for j in range(i+1, length):
if phone_book[j].startswith(phone_book[i]) or phone_book[i].startswith(phone_book[j]):
return False
return answer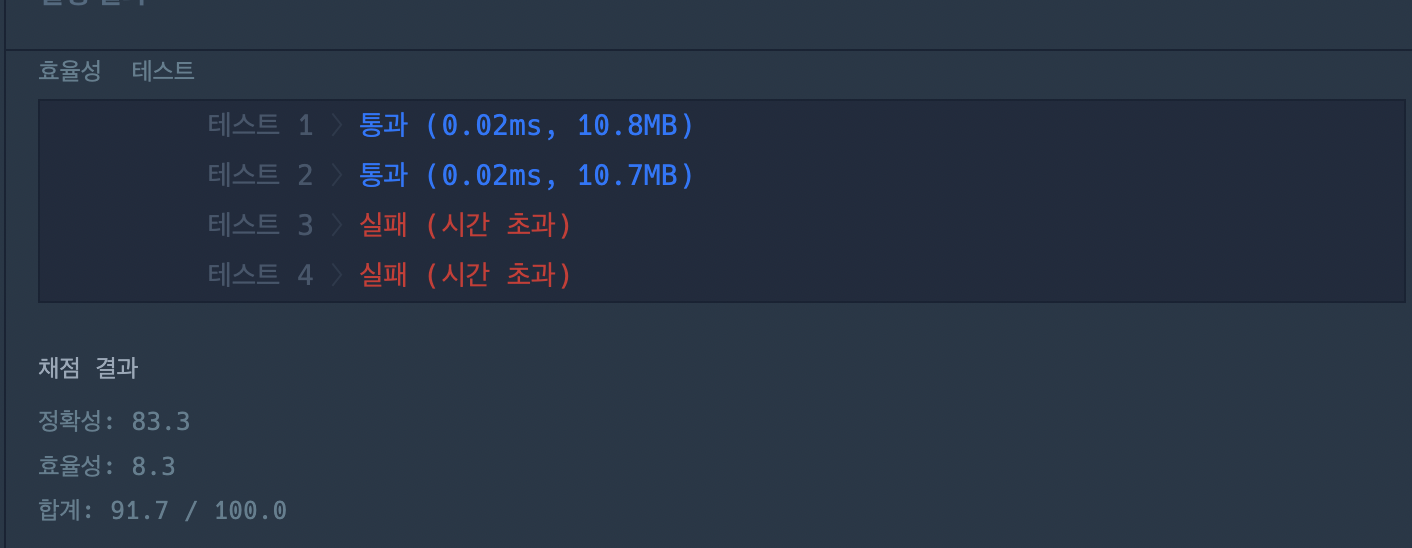
결과는 역시 정확성은 모두 통과했지만 효율성 테스트에서 통과를 하지 못했다.

그리고 프로그래머스는 위에 어떤 알고리즘으로 풀어야하는 지
위에 이미지처럼 나와있는 경우가 있는데 실수로 봐버려서 해시 문제구나 싶었다.
근데 이걸 봐도 어떻게 풀어야 할 지 감이 안잡혔다.
def solution(phone_book):
phone_book_dict = {}
for phone_numbers in phone_book:
for i in range(len(phone_numbers)):
if phone_book_dict.get(phone_numbers[:i+1]):
phone_book_dict[phone_numbers[:i+1]].append(phone_numbers)
else:
phone_book_dict[phone_numbers[:i+1]] = [phone_numbers]
for phone_numbers in phone_book:
if len(phone_book_dict[phone_numbers]) >=2:
return False
return True
에잇 그래도 해시스럽게 뭐라도 해보자 싶어서 짠 코드
phone_book에 있는 전화 번호들 각각에 대해서 해시로 저장해두고
예를들어서 phone_book이 [12, 123] 이라면
phone_book_dict = {
1: [12, 123], #1로 시작하는 전화 번호들
12: [12, 123], # 12로 시작하는 전화 번호들
123: [123]
}이런 식으로 저장 해둔다.
그리고 phone_book에 있는 전화번호를 키로 접근해서
요소가 2개 이상 있는 리스트가 있으면 False를 리턴하고 없으면 True를 리턴하는 식이다.
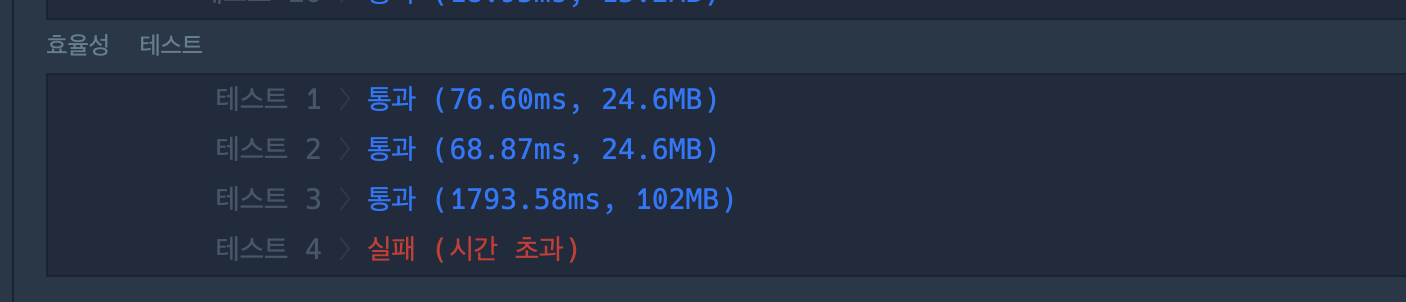
그랬더니 효율성 하나 더 통과했다.
위의 코드를 짜면서
가장 짧은 전화번호 길이보다 짧으면 dict의 키로 굳이 저장할 필요 없다라는 생각이 들었었다.
phone_book_dict = {
1: [12, 123], #1로 시작하는 전화 번호들
12: [12, 123], # 12로 시작하는 전화 번호들
123: [123]
}예를 들어서 여기 1로 시작하는 전화번호들은 굳이 알 필요가 없다.
그래서 dict에 가장 짧은 전화번호 보다 길거나 같은 것들 만 key로 저장되도록 했다.
def solution(phone_book):
answer = True
phone_book_dict = {}
phone_book.sort(key=len) #길이 순으로 sort
start = len(phone_book[0]) - 1 # 가장 짧은 전화번호 길이 - 1
for phone_numbers in phone_book:
for i in range(start, len(phone_numbers)): # 가장 짧은 전화번호
if phone_book_dict.get(phone_numbers[:i+1]):
phone_book_dict[phone_numbers[:i+1]].append(phone_numbers)
else:
phone_book_dict[phone_numbers[:i+1]] = [phone_numbers]
for phone_numbers in phone_book:
if len(phone_book_dict[phone_numbers]) >=2:
return False
return True그랬더니 통과가 됐다.
추가적으로 dict의 값들을 리스트로 저장하지 말고 개수를 저장하면 시간이 줄어들겠다 싶어서
그렇게 바꿨다.
phone_book_dict = {
1: 2, # 1로 시작하는 전화번호 개수
12: 2,
123: 1
}예를들어서 위처럼 저장되게 된다.
def solution(phone_book):
phone_book_dict = {}
phone_book.sort(key=len)
start = len(phone_book[0]) - 1
for phone_numbers in phone_book:
for i in range(start, len(phone_numbers)):
if phone_book_dict.get(phone_numbers[:i+1]):
phone_book_dict[phone_numbers[:i+1]] += 1
else:
phone_book_dict[phone_numbers[:i+1]] = 1
for phone_numbers in phone_book:
if phone_book_dict[phone_numbers] >=2:
return False
return True
참고로 이 방법에서는 dict에 가장 짧은 전화번호 보다 길거나 같은 것들만
key로 저장되도록하는 부분을 빼도 시간은 더 오래걸리지만 통과가 되긴 된다.
최종 코드
def solution(phone_book):
phone_book_dict = {}
phone_book.sort(key=len)
start = len(phone_book[0]) - 1
for phone_numbers in phone_book:
for i in range(start, len(phone_numbers)):
if phone_book_dict.get(phone_numbers[:i+1]):
if phone_numbers[:i+1] in phone_book:
return False
else:
phone_book_dict[phone_numbers[:i+1]] = 1
return True
또 생각해 보니까 먼저 dict에 값을 다 할당한 다음에 길이가 2 이상인 걸 찾는 것 보다
dict에 값을 할당하는 시점에서 2이상이 되면 바로 멈춰 버리는 게
더 빠를 거라는 생각이 들어서 최종적으로 위의 코드를 완성했다.
실행 시간을 보면 확실히 줄어든 걸 볼 수 있다 뿌듯
다른 사람 풀이
해시를 이용한 풀이
def solution(phone_book):
answer = True
dic ={} #key,value형태의 딕셔너리이용
for pNumber in phone_book:
dic[pNumber] = 1 #key:폰번호 value:1
for pNumber in phone_book: #각각 폰번호마다 검사
temp=""
for num in pNumber: #폰번호를 한글자로 쪼개서 반복문 "243"이면 "2" "4" "3"
temp +=num #쪼갠 숫자를 반복문이 돌아갈 때마다 붙음
if temp in dic and temp!=pNumber: #딕셔녀리의 키로 존재하는지 검사
answer = False
return answer
구글링 해본 결과 해시를 이용한 풀이는 모두 이 로직이었다.
코드도 깔끔하고 로직도 군더더기 없어 보인다.
근데 이 풀이에서 해시가 필요한가하는 생각은 들었다.
if temp in dic and temp!=pNumber:이 부분을
if temp in phone_book and temp!=pNumber:이렇게 바꾸는 거랑 뭐가 다른 거지?하는 의문이 들었다.
그리고 이 방법은 실행 시간이 비교적 오래 걸렸다.
sort를 이용한 풀이
def solution(phoneBook):
phoneBook = sorted(phoneBook)
for p1, p2 in zip(phoneBook, phoneBook[1:]):
if p2.startswith(p1):
return False
return True
이 풀이를 보고 머리를 얻어맞은 기분이 들었다.
나도 startswith 함수를 썼었지만 효율성에서 통과가 안돼서 바로 포기했었는데,
sort를 해주면 접두어인 문자열끼리 알아서 붙게 정렬이 된다고 한다.
그리고 zip 함수를 쓰면 이중 for문 대신 깔끔하게 코드를 짤 수 있겠구나 하는 깨달음도 있었다.
