1. A* 알고리즘
A* 알고리즘에 대해 알아보기 이전에 A* 의 기반이 되는 다익스트라 알고리즘에 대해 복습을 해 보자.
다익스트라 알고리즘
특정한 노드에서 출발하여 다른 노드까지 가는 각각의 최단 경로를 구하는 알고리즘이다.
1. 방문하지 않은 노드 중에서 가장 가까운 노드를 선택한 후,
2. 선택한 노드를 거쳐서 더 짧아지는 경로가 있는 경우 대체된다.
각각의 경로에 있어 가중치가 있으며, 가중치가 적은 경로를 통해 목적지로 향하여 최단거리를 계산하는 방법이었다. 하지만 다익스트라에는 단점이 존재한다.
- 다익스트라는 목적지로 향하기 위해 모든 경로를 살피기 때문에 불필요하게 살피는 경로가 생긴다.
아래와 같이 오른쪽으로만 가면 명백히 나오는 목적지를 찾기 위해서 필요 없는 방향까지의 경로도 계산하고 있다.
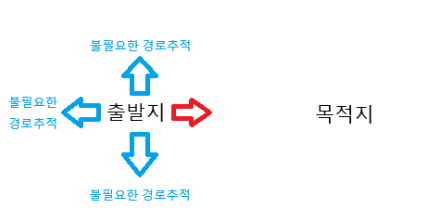
이와 같은 부분을 확장하고 개선한 알고리즘을 A* 알고리즘이라 할 수 있다.
2. 원리
A* 알고리즘의 기본이 되는 식은 아래와 같다.
f(x)=g(x)+h(x)
다익스트라 알고리즘은 f(x)=g(x) 라 할 수 있으며 A* 알고리즘은 여기어 h(x)라는 값을 추가한 것이라 할 수 있다.
여기서 g(x) 는 현재 상태의 비용을 나타낸 것을 말하고, h(x)는 휴리스틱 함수라고 부른다. A* 알고리즘의 성능은 이 휴리스틱 함수의 성능에 따라 결정된다.
그러면 간단하게 A* 알고리즘이 어떻게 돌아가는지 원리를 생각해보자.
2.1 상하좌우 이동만 가능한 경우
f(x)는 총 예상되는 거리, g(x)는 지금까지 이동한 거리, h(x)는 휴리스틱으로, 앞으로 이동할 때까지의 걸리는 거리를 계산하는 것이다.
여기에 특징이 있다면 장애물이 있다는 것인데 장애물에 대한 대처까지 어떤 식으로 진행되는지 확인해보자.
아래와 같은 상황을 생각해보자.

A* 알고리즘을 사용하는 상황에서는, 목적지를 알고 있다는 상황을 산정하고 시작한다. 따라서 h(x)는 이미 계산되어 있다고 생각하면 된다. 유클리드 거리를 기준으로 한다면 장애물이 있는 상황은 산정되어 있지 않으므로, h(x)는 출발지에서 목적지까지의 직선 이동 거리, 40이라 할 수 있다.(한 칸을 10으로 산정)
그러면 시작점을 기준으로 우선 4방향을 살펴보자.
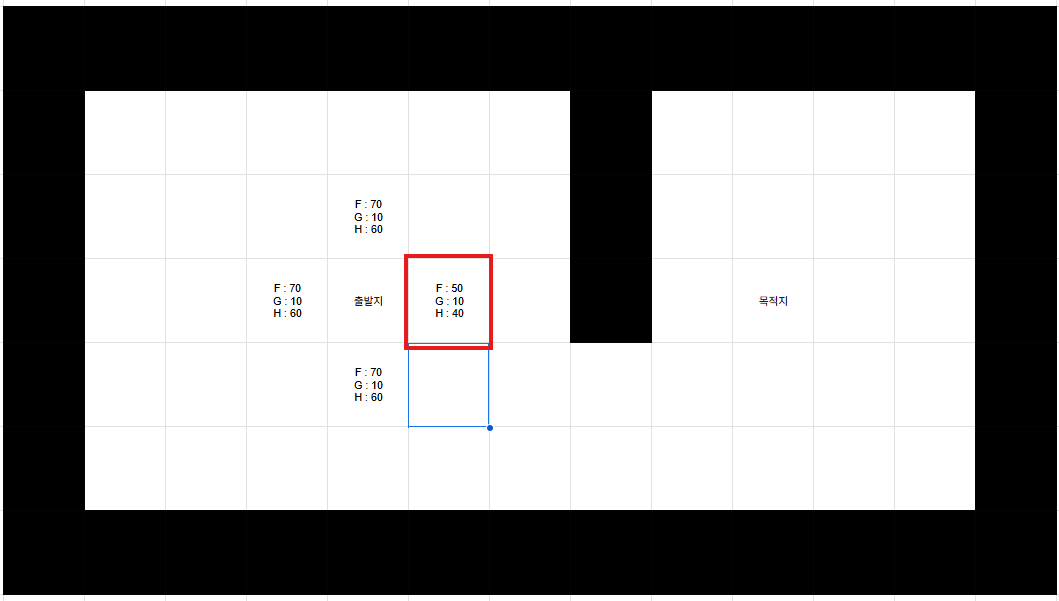
오른쪽으로 가는 방향이 무조건 제일 빠르다는 걸 우리는 직관적으로 알 수 있다. 다만 이를 컴퓨터에 이해시키기 위해서, 우리는 {이동한 거리(G)} + {제일 빠를 것으로 예상되는 거리(H)}의 합(F)으로 최단거리를 판단하게 한다. 여기서 수치적으로 F = 50인 경우가 제일 빠르므로, 나머지 경로는 전부 무시하게 된다.
그러면 이제 도착한 저 지점에서 다시 4방향을 보고, 최단거리를 선택하여 진행하게 된다. 이와 같은 과정을 반복했을 때 아래와 같이 결과가 나오게 된다.
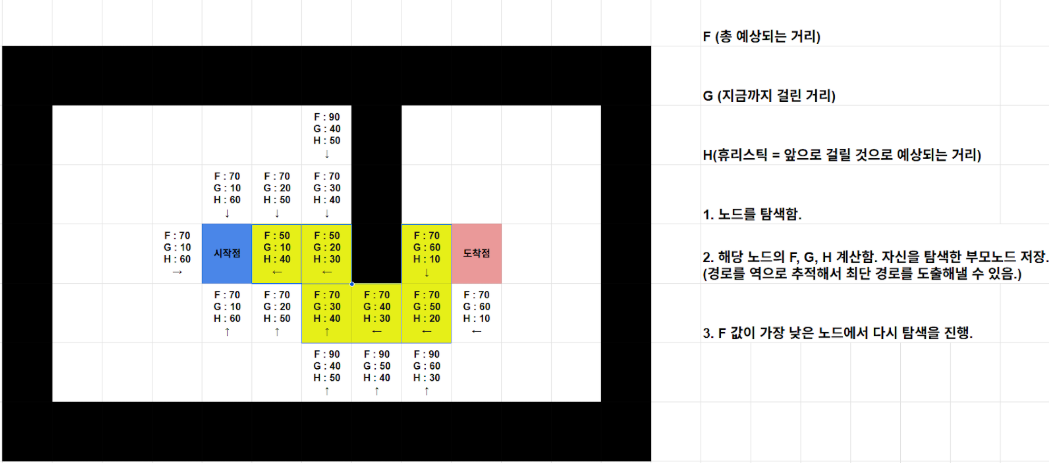
2.2 대각선 이동이 가능한 경우
대각선 이동이 가능한 경우는 대각선 이동 거리를 루트2 = 약 1.4로 산정하고 계산하면 된다.
지금의 경우 한 칸의 이동 거리를 10으로 계산하였으므로, 대각선 이동을 할 경우 14로 계산하여 최단거리를 구하면 된다.
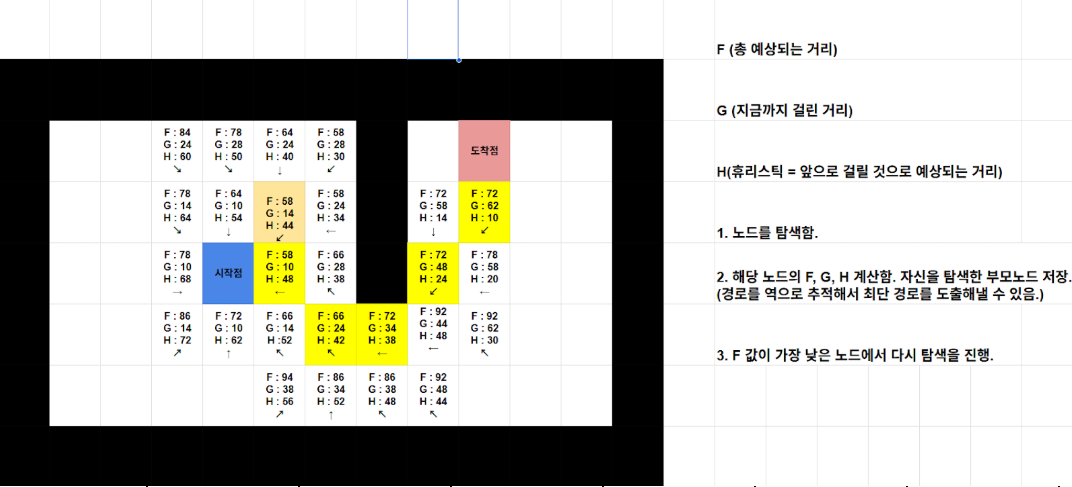
3. A* 알고리즘의 구현
A* 알고리즘을 Dictionary와 List로 구현하는 방식을 알아보려고 한다. 원리만을 알아보기 위한 코드라 효율적이지는 못하니, 효율적인 알고리즘 구현 방식에 대해서도 고민해보는 것이 좋을 것 같다.
// 탐색할 정점
public class Node
{
public float F => G + H; // 총 이동 거리 = 지금까지 걸린 거리 + 앞으로 걸릴 것이라고 예상되는 거리
public float G; // 지금까지 걸린 거리
public float H; // 앞으로 걸릴 것이라고 예상되는 거리(Heuristic)
public Node Parent; // 자신을 탐색한 노드. 탐색이 모두 종료된 후에 역추적하여 최단 경로를 도출해내기 위해서.
public Vector2Int Position; // 지금 현재 노드의 위치
public Node(Vector2Int _position)
{
Position = _position; // 생성시 위치 설정
G = float.MaxValue; // 아직 방문하지 않음
}
}
// 이동 가능한 방향 (대각선 포함 => 유클리드 거리)
private static readonly Vector2Int[] Directions = new Vector2Int[]
{
new Vector2Int(1, 0), // 오른쪽
new Vector2Int(-1, 0), // 왼쪽
new Vector2Int(0, 1), // 위
new Vector2Int(0, -1), // 아래
new Vector2Int(1, 1), // 오른쪽 위
new Vector2Int(-1, 1), // 왼쪽 위
new Vector2Int(1, -1), // 오른쪽 아래
new Vector2Int(-1, -1) // 왼쪽 아래
};
// A* 알고리즘의 의사코드
// 자료구조를 초기화
// allNodes : 위치 기반으로 노드를 저장하는 자료구조(Dictionary<Vector2Int, Node>)
// openList : 탐색할 가치가 있는 노드들을 저장할 수 있는 리스트.
// closedList : 이미 최단경로로 선택된 노드들의 위치를 가지는 리스트. 이 지점들은 다시 탐색할 필요가 없음
// 시작점에서 시작 노드를 생성.
// 시작 노드를 openList에 추가해주기.
// 반복(goal 위치에 도달할 때까지{
// openList에 노드가 들어있고, 여기에서 F값( 같을 경우 H값) 이 낮은 대로 정렬 => 우선순위 큐일 경우는 필요없을 것.
// 가장 첫번재 원소 ( =F 값과 H 값이 최소인 원소.) 현재 선택 노드로 설정.
// 해당 원소의 위치를 closedList에 추가
// 만약, 현재 선택 노드의 위치가 도착점과 같으면 최단 경로를 반환.
// Directions를 이용하여 자신을 중심으로 8방향을 판단.
// 다음으로 진행할 수 있는 방향이 이동할 수 있는 위치인지 => 장애물인지 아닌지 판단해야 함. 맵 규격에 맞는지.
// 대각선 이동이 존재할 때, 인접한 수직이나 수평 방향을 ㅗ벽이 있지 않은지도 판단해야함.
// 이동했으므로, 이동 거리를 계산.( 수직, 수평 = 1, 대각선 = 1.4)
// 휴리스틱을 계산(H값 도출)해서 F값을 도출해낸다.
// 만약에 해당 위치에 노드가 없다면 노드 생성.
// 이동거리가 기존의 이동거리보다 작다면 G에 할당해주어야 함. => H값 그리고 부모 노드를 할당해준다.
// openList에 해당 노드가 없다면 추가.
// }그러면 최단 경로를 찾는 코드를, 위의 의사코드대로 작성해 보자.
- FindPath 함수
public static List<Vector2Int> FindPath(bool[,] map, Vector2Int start, Vector2Int goal)
{
Dictionary<Vector2Int, Node> allNodes = new Dictionary<Vector2Int, Node>();
List<Node> openList = new List<Node>();
List<Vector2Int> closedList = new List<Vector2Int>();
Node startNode = new Node(start) { G = 0, H = Heuristic(start, goal);
openList.Add(startNode);
allNodes[start] = startNode;
while(openList.Count > 0)
{
openList.Sort((a, b) =>
{
int fComparison = a.F.CompareTo(b.F);
if(fComparison == 0)
return a.H.CompareTo(b.H);
return fComparison;
}
);
Node currentNode = openList[0];
openList.RemoveAt(0);
closedList.Add(currentNode.Position);
if(currentNode.Position == goal)
{
return BuildPath(currentNode);
}
foreach(Vector2Int dir in Direction)
{
Vector2Int nextPos = currentNode.Position + dir;
if(!IsValid(map, nextPos) || closedList.Contains(nextPos))
continue;
if(Mathf.Abs(dir.x) == 1 && Mathf.Abs(dir.y) == 1)
{
Vector2Int horizontal = new Vector2Int(currentNode.Position.x + dir.x, currentNode.Position.y);
Vector2Int vertical = new Vector2Int(currentNode.Position.x, currentNode.Position.y + dir.y);
if(!IsValid(map, horizontal) && !Isvalid(map, vertical))
continue;
}
float moveCost = (dir.x == 0 || dir.y == 0) ? 1f : 1.4f;
float newG = currentNode.G + moveCost;
if(!allNodes.TryGetValue(nextPos, out Node nextNode))
{
nextNode = new Node(nextPos);
allNodes[nextPos] = nextNode;
}
if(newG < nextNode.G)
{
nextNode.G = newG;
nextNode.H = Heuristic(nextPos, goal);
nextNode.Parent = currentNode;
if(!openList.Contains(nextNode))
{
openList.Add(nextNode);
}
}
}
}
return null;
} - BuildPath 함수 - 경로 탐색
private static List<Vector2Int> BuildPath(Node endNode)
{
List<Vector2Int> pathList = new List<Vector2Int>();
Node pathNode = endNode;
while(pathNode != null)
{
pathList.Add(pathNode.Position);
pathNode = pathNode.Parent;
}
pathList.Reverse();
return pathList;
}- Heuristic 함수 - 유클리드 거리 계산
private static float Heuristic(Vector2Int a, Vector2Int b)
{
return Vector2.Distance(a, b);
}- IsValid 함수 - 경로상의 노드의 이동 가능 여부 판단
private static bool IsValid(bool[,] map, Vector2Int pos)
{
int w = map.GetLength(0);
int h = map.GetLength(1);
return pos.x >= 0 && pos.x < w && pos.y >=0 && pos.y < h && map[pos.x, pos.y];
}