(주말공부)XR 플밍 - (2) 재귀함수 (3/16)

이형원·2025년 3월 16일
XR플밍
0

XR플밍

목록 보기
11/215

심화 과제 1. 재귀함수 조사

재귀 함수는 추후 자료구조/알고리즘에서 다루게 될 개념입니다. 꼬리 재귀의 위험성 및 재귀 함수사용 시 문제가 생기지 않기 위해 어느 것에 유의하여야 하는지, 어떤 상황에서 재귀함수와 반복문을 구분해서 사용할 수 있을 지 탐구하도록 합시다.

심화 과제 2. 피보나치 함수 제작
피보나치 수란, 맨 첫째와 둘째 항은 각각 1이지만, 그 뒤로 오는 모든 항은 앞의 두 항의 합인 수열입니다. 예를 들어 [1,1,2,3,5,8,...] 이렇게 4번째(3) 항목은 2번째(1)와 3번째(2)의 합이고, 마찬가지로 6번째(8) 항목은 바로 앞 4번째(3), 5번째(5)의 합인 형태입니다. 함수의 인자값으로 '몇번째' 인지 건네주면, 일치하는 피보나치 수를 반환하는 함수를 제작하세요. 참고로 11번째 피보나치 수는 89, 20번째 피보나치 수는 6765 입니다.

1. 정의와 특징

1.1) 재귀함수 : 자신을 호출하는 함수.

while문/for문과 같은 반복문처럼, 재귀 함수도 작은 부분을 하나씩 처리한 결과를 결합해 하나의 복잡한 문제를 해결해 나가는 방법이다.

1.2) 재귀함수의 구조

  1. 기저 조건(Base Case) : 함수가 더 이상 자기 자신을 호출하지 않고 종료하는 조건
  2. 재귀 단계(Recursive Step) : 함수가 자기 자신을 호출하는 단계

1.3) 재귀함수의 특징 및 장단점

<장점>

  • 간결함과 직관성 - 코드를 더 간결하고 직관적으로 작성할 수있다.
  • 문제 분할 - 반복문(for/while)에 비해 코드를 더 짧게 구현할 수 있는 경우 가 많다.

<단점>

  • 설계와 테스트 난이도가 어려움
  • 스택 메모리 사용으로 인한 오버헤드 - 호출될 때마다 스택에 새로운 프레임을 생성하고, 메모리를 사용하기에, 스택 오버플로우 같은 문제가 발생할 수 있음.
  • 성능 - 반복문으로 변환할 수 있는 경우 반복문에 비해 성능이 떨어질 수 있다.

* 오버헤드 : 어떤 처리를 하기 위해 들어가는 간접적인 처리 시간, 메모리 등
* 스택 오버플로우 : 1) 변수의 크기가 stack보다 크거나, 2) 함수를 무한 호출하고 있거나, 3) 변수가 Stack을 넘어가 다른 곳에 위치할 때 발생하는 오류

2. 재귀함수를 이용한 팩토리얼 구하기(예시1)

2.1) 팩토리얼(factorial)

수학에서의 자연수의 계승, 1부터 n까지의 모든 자연수를 곱한 값이다. '!'로 기호를 표시한다.

ex) 4! = 4 * 3 * 2 * 1 = 24

2.2) 재귀함수를 이용한 팩토리얼 계산

팩토리얼 계산을 위한 함수는 아래와 같이 만들 수 있다.

static int Factorial(int n)		// 팩토리얼 계산 함수
{
    if (n == 0)
    {
        return 1;
    }
    return n * Factorial(n - 1);
}

static void Main(string[] args)
{
    Console.Write("팩토리얼 계산기 - 0 이상의 정수를 입력해 주세요. : ");
    Console.WriteLine($"Factorial : {Factorial(int.Parse(Console.ReadLine()))}");
}

이와 같이 작성하고 4!의 결과를 출력해 보자.

2.3) 재귀함수의 호출 과정

위의 팩토리얼 계산 함수를 바탕으로 어떻게 재귀함수가 작동하고, 팩토리얼 값을 구했는지 살펴보자

  1. 4!의 값을 계산하기 위해 n에 4의 값이 입력되었다.
  2. 4 * Factorial(3)이 반환된다.
  3. Factorial(3)은 3 * Factorial(2)로 반환된다. (4 * (3 * Factorial(2)))
  4. Factorial(2)는 2 * Factorial(1)로 반환된다. (4 * (3 * (2 * Factorial(1))))
  5. Factorial(1)은 1 * Factorial(0)로 반환된다. (4 * (3 * (2 * (1 * Factorial(0)))))
  6. Factorial(0)은 1이므로 최종반환값은 (4 * 3 * 2 * 1 * 1) = 24이다.

3. 심화과제 2- 재귀함수를 이용한 피보나치 수열 구하기(예시2)

3.1) 피보나치 수(영어: Fibonacci numbers)

첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열.
ex) 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

3.2) 재귀함수를 이용한 피보나치 함수 계산

n = 0 일 때 0, n = 1일 때 1이라고 계산하고 기저조건을 아래와 같이 설정하였다.

static int Fibonacci(int n)
{
	if (n == 0)
    {
    	return 0;
    }
    else if (n = 1)
    {
        return 1;
    }
    return Fibonacci(n - 1) + Fibonacci(n - 2);
}

static void Main(string[] args)
{
    Console.Write("피보나치 계산기 - 0 이상의 정수를 입력해 주세요. : ");
    Console.WriteLine($"Fibonacci : {Fibonacci(int.Parse(Console.ReadLine()))}");
}

결과 출력은 아래와 같이 나온다.

  • 11번째 피보나치 수
  • 20번째 피보나치 수

결과 출력이 제대로 된 것을 확인할 수 있다.

다만 여기까지는 문제가 없어 보이지만, 아래와 같이 입력값으로 100을 입력해 주면 어떻게 될까?
큰 숫자를 입력하면 위와 같이 결과가 바로 출력되지 않고, 컴퓨터 본체에서 쿨링팬이 미친듯이 돌아가기 시작했다. 함수 호출을 너무 많이 해야 하는 나머지 지연시간이 발생하여 결과 출력이 늦어지는 것이다.
그렇다면 이렇게 큰 숫자는 컴퓨터로 계산하는 건 불가능한 걸까? 이를 해결할 수 있는 방법을 생각해 보았다.

4. 꼬리 재귀

4.1) 꼬리재귀 : 재귀호출이 끝나면 아무 일도 하지 않고 결과만 바로 반환하도록 하는 방법.

재귀함수의 장점은 살리고, 단점은 보완하는 최적화의 방법 중 하나다.

정의만으로는 썩 잘 이해가 가지 않았기 때문에 우선은 적용 예시부터 살펴봤다.

4.2) 꼬리 재귀함수를 적용한 팩토리얼 계산

static int Factorial(int n)
{
    if (n == 0)
    {
        return 1;
    }
    return n * Factorial1(n - 1);
}

처음 만들었던 팩토리얼 계산기는 위와 같았다. 이걸 꼬리 재귀함수 방식으로 바꾸면 다음과 같이 변한다.

static int FactorialTail(int n, int accumulator = 1)	// n번 누적 곱셈값을 반환
{
    if (n == 0)
    {
    return accumulator;
    }
    return FactorialTail(n - 1, accumulator * n);
}

static int Factorial(int n)
{
    return FactorialTail(n, 1);

}

static void Main(string[] args)
{
    Console.Write("팩토리얼 계산기 - 0 이상의 정수를 입력해 주세요. : ");
    Console.WriteLine($"Factorial : {Factorial(int.Parse(Console.ReadLine()))}");
}

팩토리얼 함수를 두 개로 분리하여, 재귀 호출 이후 추가적인 연산을 요구하지 않도록 구현한 것이다. 똑같이 4!를 넣으면 아래와 같이 결과가 출력된다.

원하는 결과가 나오긴 했지만 이 계산 과정이 쉽게 와닿지 않았다.

꼬리 재귀함수가 어떤 식으로 진행되는 건지 조금 더 뜯어보자.

4.3) 꼬리 재귀함수의 호출 과정

재귀함수로 만든 팩토리얼 함수의 진행 방식은 아래와 같았다.

  1. 4!의 값을 계산하기 위해 n에 4의 값이 입력되었다.
  2. 4 * Factorial(3)이 반환된다.
  3. Factorial(3)은 3 * Factorial(2)로 반환된다. (4 * (3 * Factorial(2)))
  4. Factorial(2)는 2 * Factorial(1)로 반환된다. (4 * (3 * (2 * Factorial(1))))
  5. Factorial(1)은 1 * Factorial(0)로 반환된다. (4 * (3 * (2 * (1 * Factorial(0)))))
  6. Factorial(0)은 1이므로 최종반환값은 (4 * 3 * 2 * 1 * 1) = 24이다.

이에 반해 꼬리 재귀함수로 만든 팩토리얼 함수의 진행 방식은 다음과 같다.

  1. 4!의 값을 계산하기 위해 n에 4의 값이 입력되었다.
  2. FactorialTail(4, 1)이 반환된다.
  3. FactorialTail(4, 1)은 FactorialTail(3, 1*4) = FactorialTail(3, 4)로 반환된다.
  4. FactorialTail(3, 4)는 FactorialTail(2, 4*3) = FactorialTail(2, 12)로 반환된다.
  5. FactorialTail(2, 12)는 FactorialTail(1, 12*2) = FactorialTail(1, 24)로 반환된다.
  6. FactorialTail(1, 24)는 FactorialTail(0, 24*1) = FactorialTail(0, 24)로 반환된다.
  7. FactorialTail(0, 24)는 24로 반환된다.

두 방식의 차이점은 텍스트로만 봤을 때에도 차이가 나는 것이 보인다.
재귀함수에서는 무한정 괄호 속으로 들어가 계산하는 과정 때문에 메모리 소모가 많은 반면에,
꼬리 재귀함수는 계산값을 반환해 주는 함수를 추가하여 계산값을 저장하기 위한 추가적인 메모리 사용 과정을 없앴다.

이러한 이유로 큰 수를 입력했을 경우 메모리 사용량을 줄여주고 지연시간이 발생하지 않는다.

이걸 피보나치 함수에도 똑같이 적용해보자.

4.4) 꼬리 재귀함수로 표현한 피보나치 함수 계산

기존의 재귀함수로 표현한 피보나치 함수를 꼬리 재귀함수로 나눠야 하는데,
재귀함수의 단점으로 언급했던 설계와 테스트의 어려움을 몸소 경험했다.
오랫동안 고민과 테스트 과정을 거친 끝에 꼬리 재귀함수 형태로 바꿀 수 있었다.

// n번과 (n-2번째 값)과 (n-1번째 값)을 압력하고 그 합을 반환함.
static int FibonacciTail(int n, int twoPrevFibo = 0, int prevFibo = 1) 
    {            
        if (n == 0)
        {
            return 0;
        }
        else if (n == 1)
        {
            return prevFibo;
        }
        return FibonacciTail(n - 1, prevFibo, twoPrevFibo + prevFibo);
    }

    static int Fibonacci(int n)
    {
        return FibonacciTail(n, 0, 1);
    }

    static void Main(string[] args)
    {
        Console.Write("피보나치 계산기 - 0 이상의 정수를 입력해 주세요. : ");
        Console.WriteLine($"Fibonacci : {Fibonacci(int.Parse(Console.ReadLine()))}");
    }
}

이와 같이 꼬리 재귀함수로 피보나치 수열을 만든 후, 다시 100번째 피보나치 수를 계산해 보았다.
오버플로우로 이상한 숫자가 나오기는 했지만, 결과 출력은 일단 가능해졌다.

5. 결론

이렇듯 재귀함수 및 꼬리 재귀함수란 무엇이고, 재귀함수로 무엇을 할 수 있는지 알게 되었다.

  1. 재귀함수(꼬리 재귀함수)는 자신을 호출하는 함수로, 반복문 외의 방법으로 코드를 작성하는 방법이다.
  2. 재귀함수(꼬리 재귀함수)를 사용하기 위해선 기저 조건과 재귀 단계를 잘 설계해야 한다.
  3. 재귀함수(꼬리 재귀함수)는 간결하고 직관적으로 문제를 해결할 수 있지만, 설계가 어렵고 스택 오버플로우와 성능 저하 등의 문제를 일으킬 수 있다.
  4. 재귀함수로 팩토리얼 계산과 피보나치 수열 계산을 해 보았다.
  5. 꼬리 재귀함수로 재귀함수의 단점을 보완하고 장점을 극대화할 수 있다.

그러면 꼬리 재귀함수로 모든 문제가 해결되느냐, 아쉽게도 그건 아닌 것 같았다.
아래의 결과를 참고해 보도록 한다.
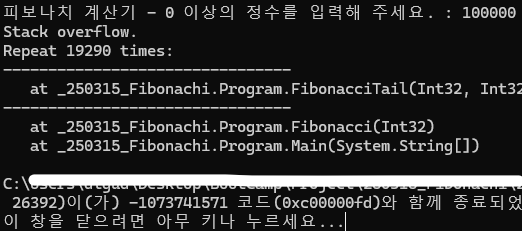꼬리 재귀함수로 작성한 피보나치 수열에 100,000번째 숫자 계산을 시켜 보았다. 꼬리 재귀함수로도 스택 오버플로우는 피할 수가 없다는 사실을 알게 되었다.
이와 같이 재귀함수의 장점과 단점, 한계를 이해하고 어떤 상황에서 재귀함수를 사용할지, 반복문을 사용해야 할지 판단이 필요해 보인다.

참고자료 :
https://jettstream.tistory.com/431#google_vignette
https://nybot-house.tistory.com/116#google_vignette

https://velog.io/@dldhk97/%EC%9E%AC%EA%B7%80%ED%95%A8%EC%88%98%EC%99%80-%EA%BC%AC%EB%A6%AC-%EC%9E%AC%EA%B7%80
https://jettstream.tistory.com/433#%EA%BC%AC%EB%A6%AC_%EC%9E%AC%EA%B7%80(tail_recursion)%EB%9E%80_%EB%AC%B4%EC%97%87%EC%9D%B8%EA%B0%80?

profile
이형원
게임 만들러 코딩 공부중
이전 포스트

(주말공부)XR 플밍 - (1) 다이아몬드 별 찍기 (3/15)

다음 포스트

XR 플밍 - 1. 프로그램 언어 기초 (5-1) - 배열 (3/17)

0개의 댓글