RB 트리의 삭제 개념
-
삽입 전 RB 트리의 속성을 만족한 상태여야 한다.
-
삭제 방식은 일반적인 BST(이진탐색트리)와 동일하다.
-
원하는 노드 삭제 이후, 삭제되는 색을 통해 RB 트리 속성 위반 여부를 확인한다.
-
RB 트리 속성을 위반했다면 트리를 재조정(delete-fixup)한다.
-
RB 트리의 속성을 만족한다면 삭제 종료.
삭제되는 색의 결정
-
삭제하려는 노드의 자녀가 없거나 하나라면, 삭제되는 색은 삭제되는 노드의 색
-
삭제하려는 노드의 자녀가 둘이라면, 삭제되는 색은 삭제되는 노드의 successor의 색
successor?
-
임의의 노드 X의 오른쪽 서브트리가 존재하는 경우, 오른쪽 서브트리의 최소값을 가진 노드를 의미한다.
-
반면에 오른쪽 서브트리가 존재하지 않을 때는, 부모를 따라 올라가며 탐색한다. 탐색하는 노드가 부모의 왼쪽 노드일 경우, 탐색하는 노드의 부모 노드가 successor 노드가 된다.
-
RB 트리의 경우에는 두 자식이 모두 있는 경우에만 successor 노드를 찾는 과정을 필요로 한다. 따라서 RB트리에서의 successor 노드의 정의는 오른쪽 서브트리의 최솟값이라고 생각하면 된다.
삭제되는 색이 RED인 경우
-
어떠한 속성도 위반하지 않는다. 왜?
-
루트 노드와 NIL 노드는 BLACK, 따라서 삭제되는 색이 RED라면 이 둘은 삭제되지 않았다는 뜻 -> 2, 3번 위반 X
-
삭제되는 색이 RED라면 BLACK들은 지워지지 않음. 삭제한다고 RED가 연속해서 나오지도 않고, NIL노드까지의 BLACK 수에도 영향을 끼치지 않음 -> 4, 5번 위반 X
삭제되는 색이 BLACK인 경우
- 2, 4, 5번 속성을 위반할 수 있음
2번 속성을 위반하는 경우
- 그냥 루트 노드를 BLACK으로 바꿔주면 된다.
5번 속성을 위반하는 경우
-
거의 대부분의 경우 5번을 위반하게 된다. BLACK노드를 지웠으니 어찌보면 당연한 얘기!
-
삭제된 색의 위치를 대체한 노드에 EXTRA BLACK을 부여한다. 이 EXTRA BLACK은 경로에서 BLACK을 카운트 할때 BLACK 노드 취급함.
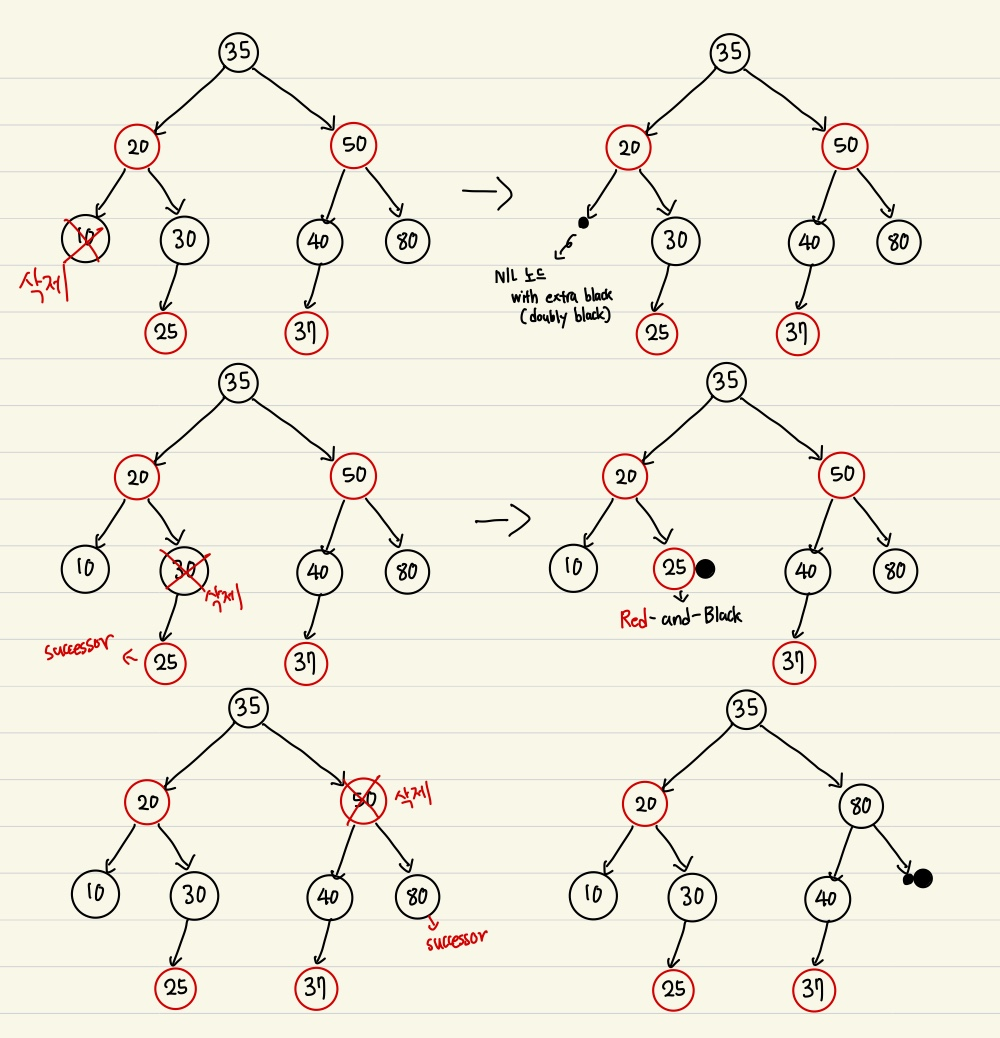
-
EXTRA BLACK의 부여 예시들. EXTRA BLACK을 부여받은 노드는 DOUBLY BLACK or RED-AND-BLACK이 된다.
RED-AND-BLACK 의 처리
- 그냥 RED-AND-BLACK노드를 BLACK으로 바꿔주면 해결
DOUBLY BLACK 의 처리
- 이녀석이 관건. 총 네개의 케이스로 나뉜다.
Case 1
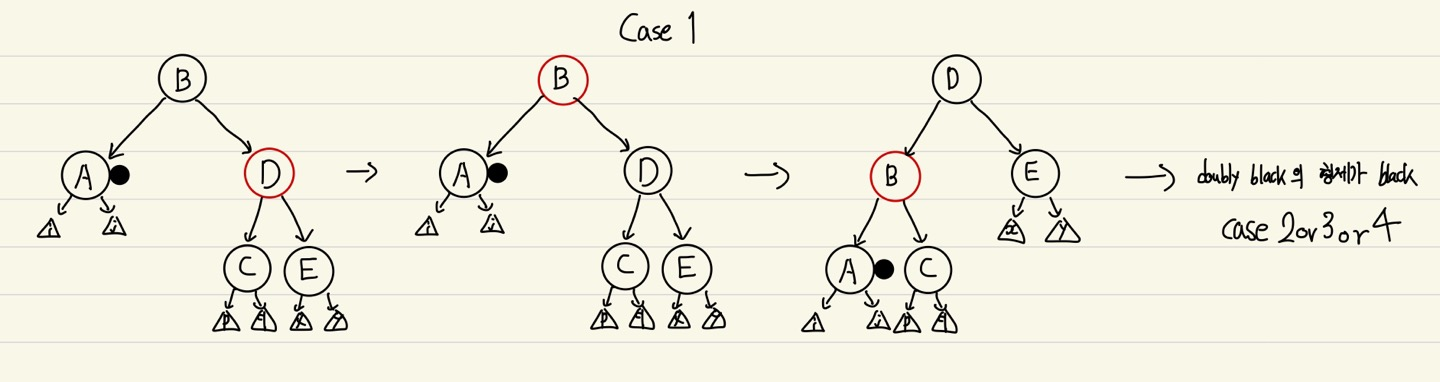
- DOUBLY BLACK의 형제가 RED일 때
- DOUBLY BLACK의 형제와 부모의 색을 바꿔주고, 부모를 기준으로 왼쪽 회전
- DOUBLY BLACK의 형제가 BLACK으로 바뀜 -> Case2 or 3 or 4
Case 2
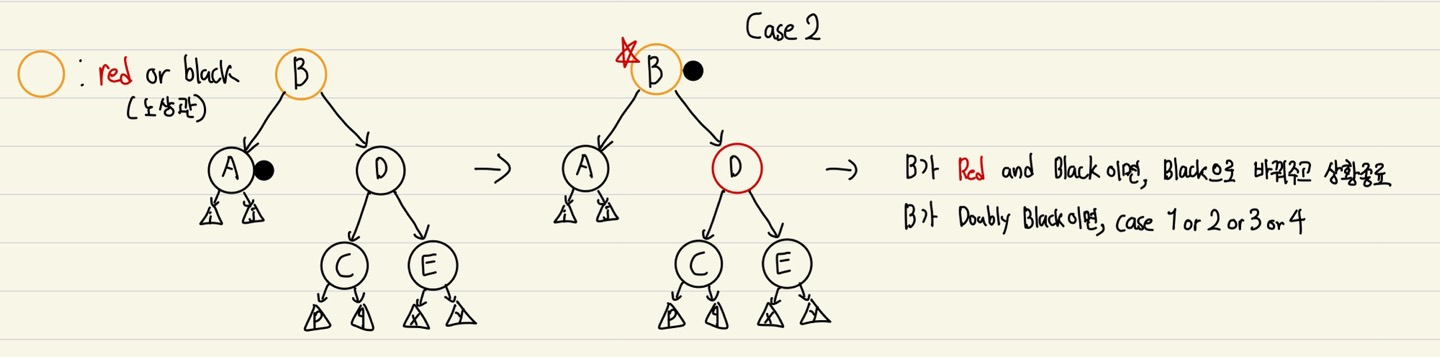
- DOUBLY BLACK의 형제가 BLACK, 형제의 자식이 모두 BLACK
- DOUBLY BLACK과 형제의 BLACK을 부모로 넘겨줌. DOUBLY BLACK 은 BLACK, 형제는 RED로 변한다.
- 부모가 RED라면 RED-AND-BLACK, BLACK으로 만들면 상황종료
- 부모가 BLACK이라면 부모의 기준으로 Case 1 or 2 or 3 or 4
Case 3
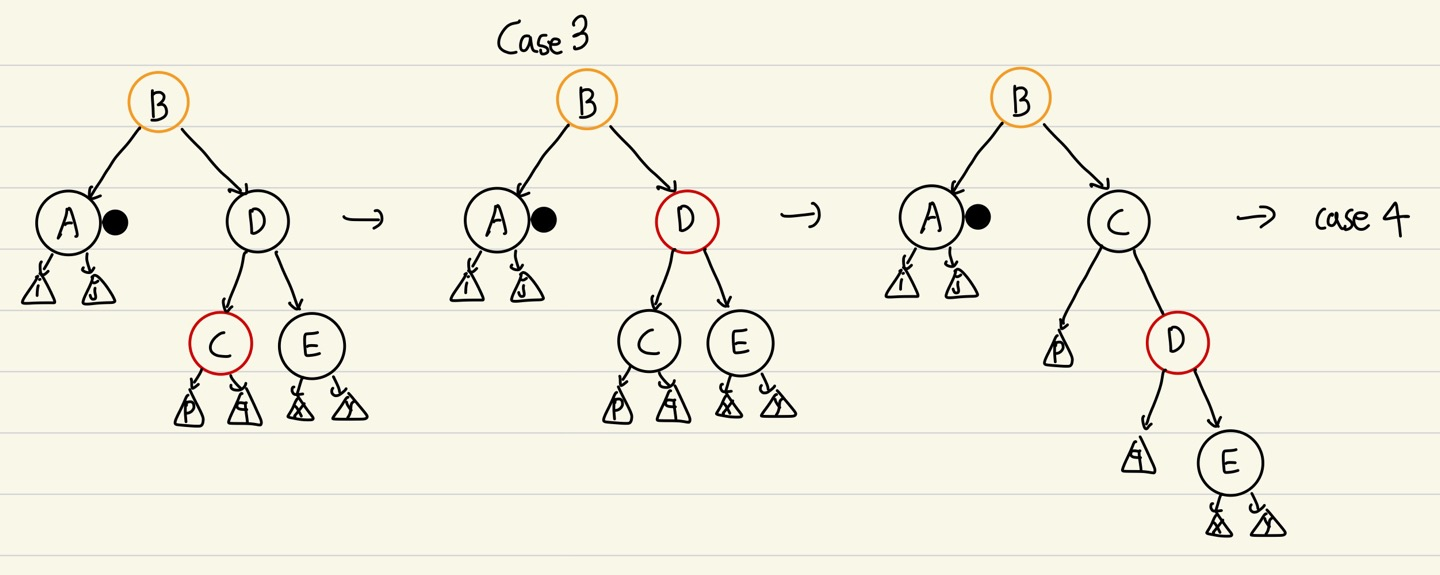
- DOUBLY BLACK의 형제가 BLACK, 형제의 왼쪽 자식이 RED, 오른쪽 자식은 BLACK
- DOUBLY BLACK의 형제와 왼쪽 자식의 색을 바꿔줌
- DOUBLY BLACK의 형제를 기준으로 오른쪽 회전
- 이후 Case 4로 해결
Case 4
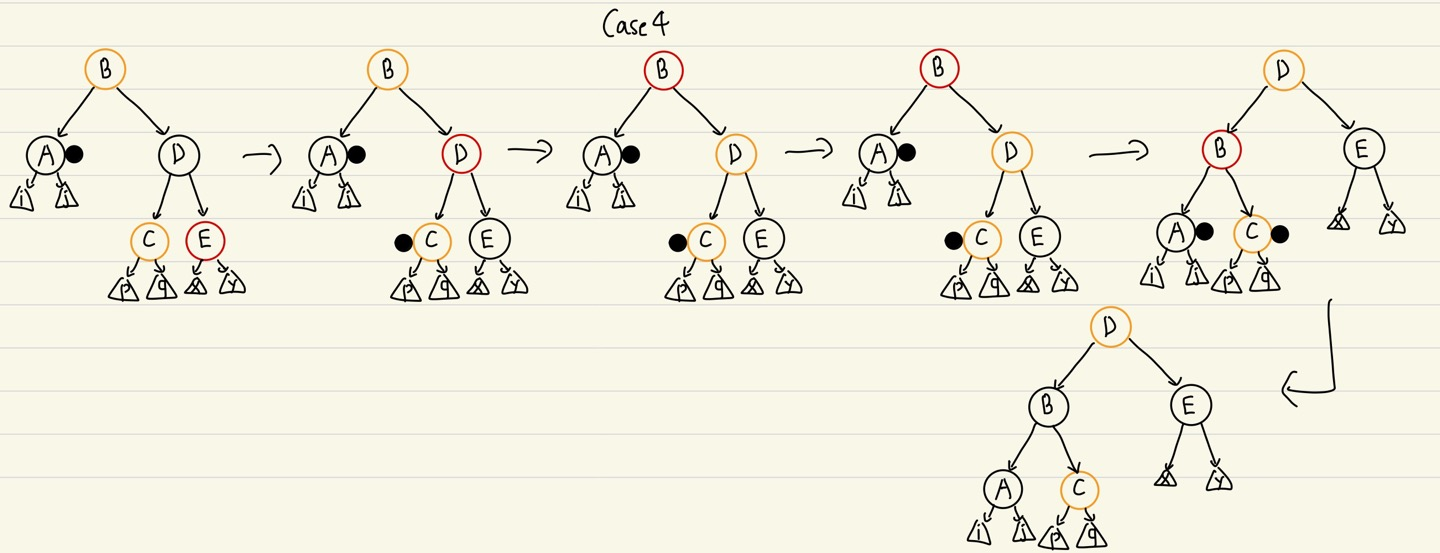
- DOUBLY BLACK의 형제가 BLACK, 형제의 오른쪽 자식이 RED
- DOUBLY BLACK의 형제를 부모의 색으로, 형제의 오른쪽 자녀는 BLACK으로, 부모는 BLACK으로 바꾼 후에 부모를 기준으로 왼쪽으로 회전
의사 코드 예시
while (타겟이 루트아님 && 타겟 == BLACK) {
// CASE 1.
if 형제 == RED
형제/부모 서로 색바꾸기, 부모기준 회전 (타겟이 내려가도록)
// CASE 2.
if 형제 == BLACK, 형제의 자식 둘다 블랙
형제/자신의 블랙을 부모로 올리기 -> 형제를 RED로 변경, 부모에서 다시 fixup
else {
// CASE 3.
if 형제 == BLACK, 부모/형제/(형제의 꺾인 자식) == RED
자식 RED와 형제 서로 색바꾸기, 펴지게 회전 (RED가 바깥쪽에 오게)
CASE 4가 됨
// CASE 4. 형제 == BLACK, 부모/형제/(형제의 펴진 자식) == RED
부모/형제 서로 색바꾸기
형제의(펴진 자식) = BLACK
부모기준 회전 (타겟이 내려가도록)
타겟을 루트로 설정 -> while 종료
}
}
// 종료전
타겟을 BLACK으로 변경