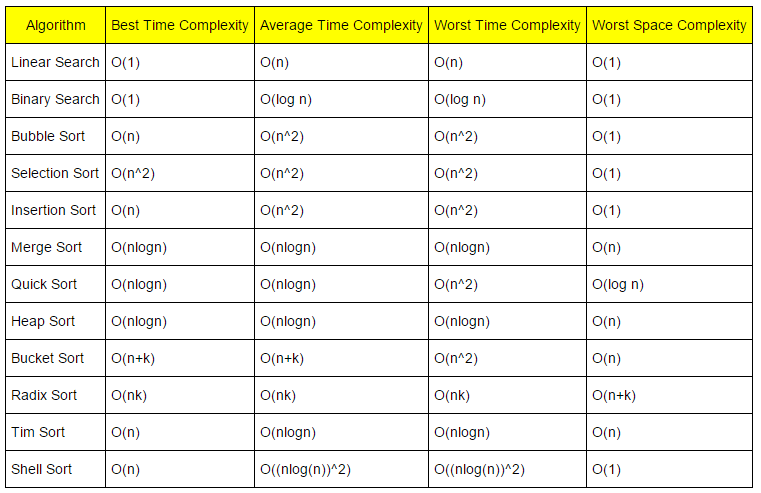
- 각 정렬 알고리즘의 시간, 공간 복잡도 표
삽입 정렬(Insertion Sort)
- 내가 구현해 본 삽입 정렬
def whereToInsert(arr, start):
for i in range(1, start + 1):
try:
if arr[start-i] <= arr[start]:
return start - i + 1
except:
pass
return 0
# 1부터 끝까지 sorting 수행
sortCount = 1
while sortCount < len(numbers):
if sortCount == whereToInsert(numbers, sortCount):
sortCount += 1
pass
else:
numbers.insert(whereToInsert(numbers, sortCount), numbers[sortCount])
del numbers[sortCount+1]
sortCount += 1
for i in range(len(numbers)):
print(numbers[i])-
배열의 각 요소마다, 리스트 처음까지 돌아오며 알맞은 자리를 찾아 삽입(insert)해주는 방식.
-
이미 어느정도 정렬된 데이터를 재정렬할 때 빠르며, 안정한 정렬 방법이다. 또한, 동작이 간단하다.
-
하지만 일반적으로는 시간복잡도가 좋지 않아 잘 쓰이지 않는 sort
도수 정렬(Counting Sort)
- 내가 구현해 본 도수 정렬
distribute = [0]*10001
for i in range(count):
num = int(sys.stdin.readline())
distribute[num] += 1
for i in range(len(distribute)):
if distribute[i] == 0:
pass
else:
for _ in range(distribute[i]):
print(i)-
데이터의 도수 분포를 이용하여 정렬
-
값들의 비교를 일절 하지 않는다는 특이점
-
동작이 간단하며 범위가 정해져있다면 시간복잡도가 좋다. 이중 반복문이나 재귀 등을 사용하지 않음!, 또 안정적인 정렬이다.
-
하지만 데이터가 일정해야 한다는 것과, 데이터의 범위 역시 알고 있어야 한다는 단점이 있다.
퀵 정렬
- 내가 구현해 본 퀵 정렬
def quickSort(arr, start, end):
leftPointer = start
rightPointer = end
middle = arr[(start+end)//2]
while leftPointer <= rightPointer:
# 포인터 움직여가며 그 위치에 알맞지 않은놈 두놈 골라서
while arr[leftPointer] < middle:
leftPointer += 1
while arr[rightPointer] > middle:
rightPointer -=1
# 둘이 바꿔버림
if leftPointer <= rightPointer:
arr[leftPointer], arr[rightPointer] = arr[rightPointer], arr[leftPointer]
# print(arr)
leftPointer += 1
rightPointer -= 1
if start < rightPointer: quickSort(arr, 0, rightPointer)
if leftPointer < end: quickSort(arr, leftPointer, end)
quickSort(numbers, 0, len(numbers)-1)
for i in range(len(numbers)):
print(numbers[i])-
기준점(Pivot)을 기준으로 반복하여 좌우로 나눠주며 정렬하는 방식
-
대부분의 상황에서 손꼽히는 속도와 추가적인 배열을 생성하지 않아 공간복잡도도 우수한, 그야말로 팔방미인 정렬
-
하지만 완벽할 수는 없는건가? 불안정 정렬에 속한다
-
오히려 정렬된 요소들에서는 효율이 떨어진다는 특이점.
