트리 자료구조에 대해 알아보자

트리란?

• 특정한 특성을 가지는 그래프의 일종으로서, 그 자체로 독립된 자료구조로 쓰인다.

• 트리의 대표적인 특성들은 다음과 같다.

사이클이 없음 (Cycle-Free): 트리는 사이클이 존재하지 않는 그래프입니다. 즉, 두 노드를 잇는 경로가 유일하며, 자기 자신으로의 순환 경로가 존재하지 않습니다.

연결되어 있음 (Connected): 트리의 모든 노드는 서로 연결되어 있어야 합니다. 즉, 어떤 노드에서 다른 모든 노드로 가는 경로가 존재해야 합니다.

단일 루트 (Single Root): 트리는 단일 루트 노드를 가집니다. 이 루트 노드는 트리의 모든 다른 노드들에게 공통된 조상 노드로서 기능하며, 트리의 시작점이 됩니다.

계층 구조 (Hierarchical Structure): 트리는 노드들 간의 계층 구조를 가집니다. 각 노드는 부모 노드와 자식 노드들로 연결되어 있어서, 부모 노드에서 자식 노드들로의 방향성이 존재합니다.

비순환적인 관계 (Acyclic Relationships): 트리는 비순환적인 관계를 가집니다. 즉, 한 노드에서 출발하여 자기 자신으로 돌아오는 경로가 존재하지 않습니다.

노드의 차수 제한 (Limited Node Degree): 트리의 각 노드는 자식 노드의 개수가 제한되어 있습니다. 일반적으로 이진 트리(binary tree)라는 형태의 트리가 가장 많이 사용됩니다. 이진 트리는 각 노드가 최대 2개의 자식 노드를 가질 수 있는 트리입니다.

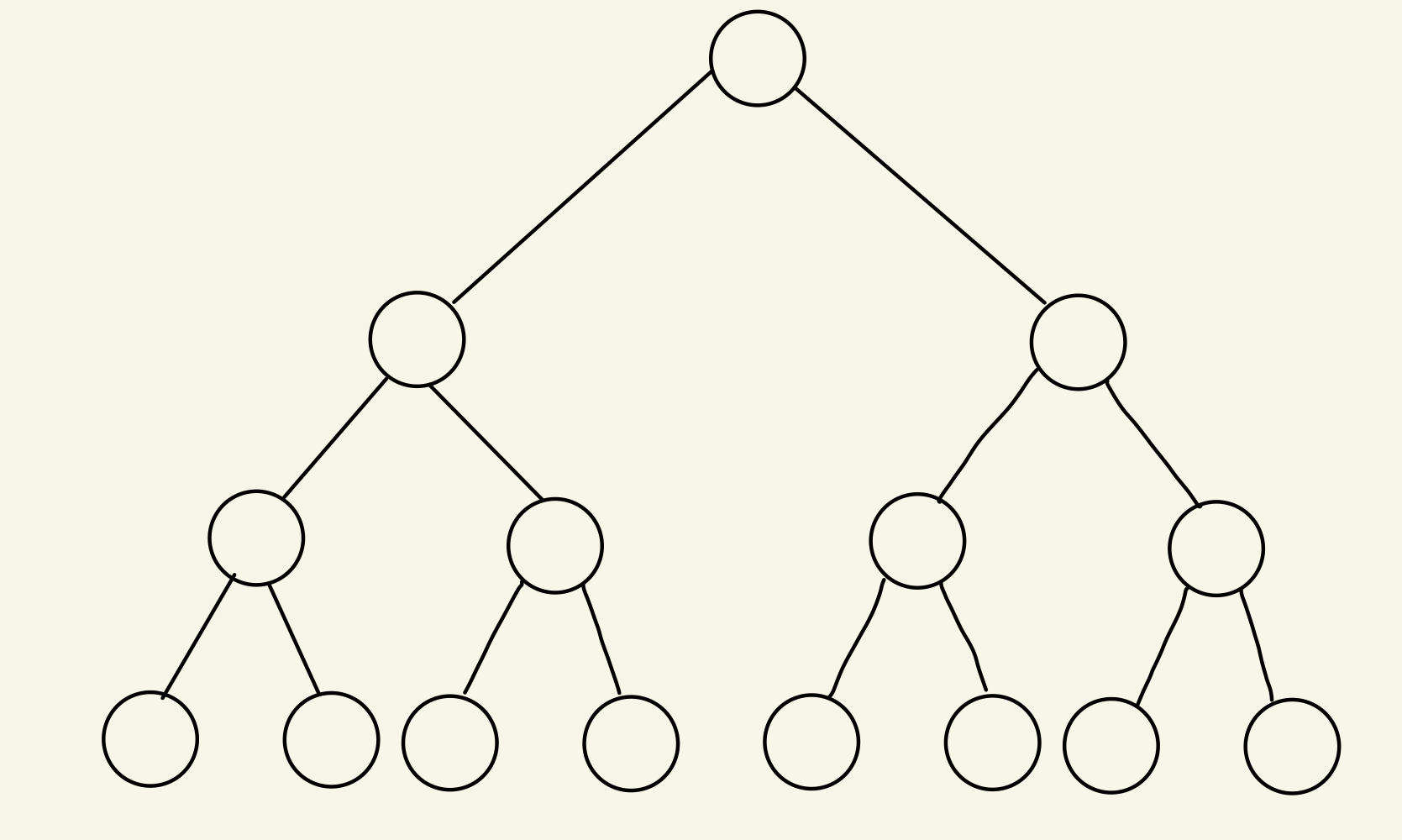
• 간단한 트리 예시