힙과 힙 정렬 +오답노트

힙

• '부모의 값이 자식의 값보다 항상 크거나 같다 or 작거나 같다'를 만족하는 완전 이진 트리 자료구조

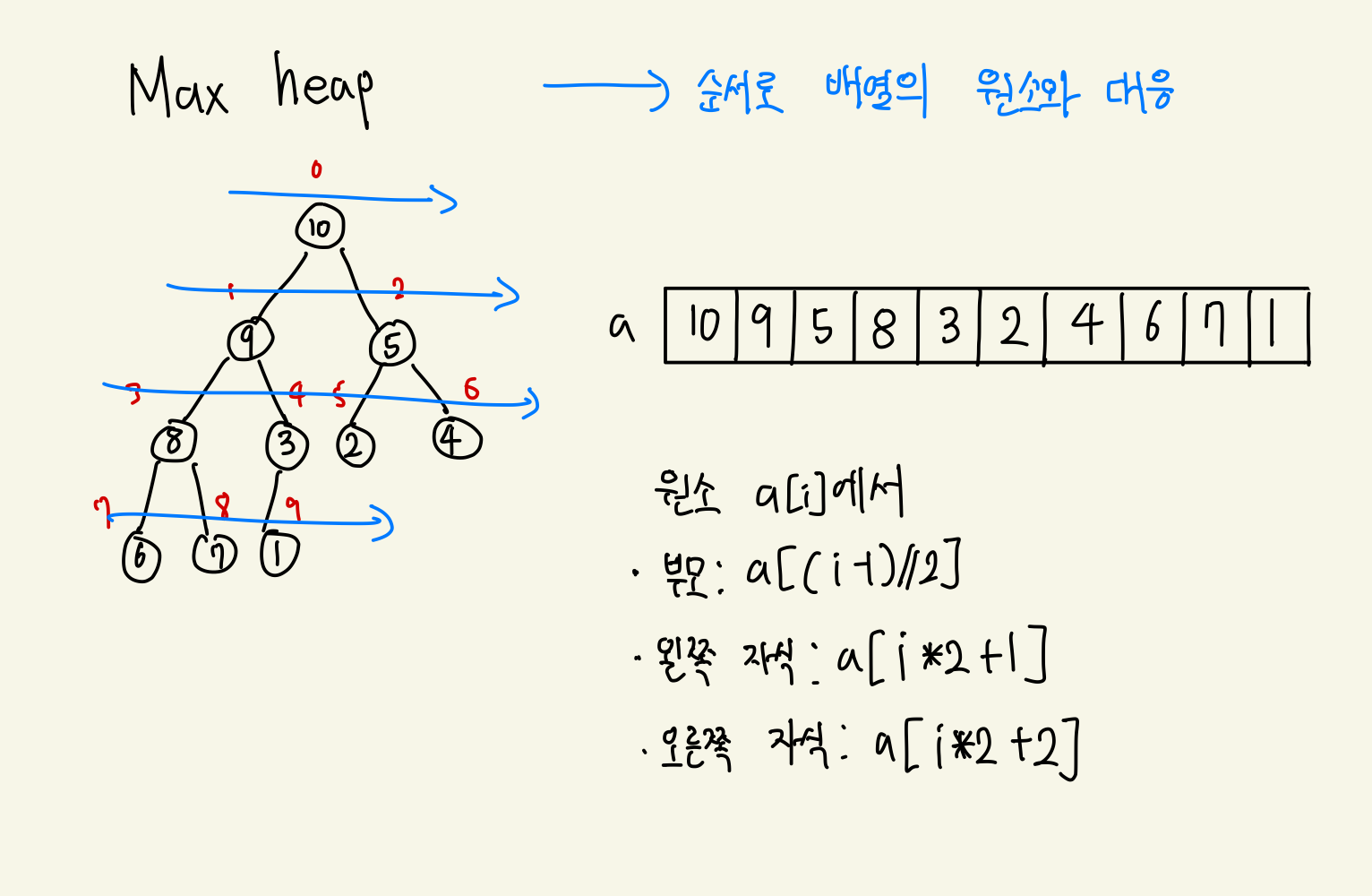
힙 정렬

• '힙에서 최댓값 or 최소값은 루트(최상위 노드)에 위치한다' 라는 특징을 이용하여 정렬하는 알고리즘

• 아래의 과정을 반복하여 정렬

1. 힙에서 최댓값인 루트를 꺼낸다. (오름차순의 경우 최솟값)
2. 루트 이외의 부분을 다시 힙으로 만든다.

• 선택 정렬을 응용한 알고리즘으로, 시간복잡도가 O(n*2)인 선택 정렬과 달리 트리의 높이가 log(n) 전체 요소가 n개이므로 시간복잡도 - nlog2(n)

힙 생성과 힙 정렬을 직접 구현해보자 (내림차순)

import sys

N = int(sys.stdin.readline())
heap = []

def heapAdd(value):
    global heap
    heap.append(value)
    elem = len(heap)-1
    while True:
        if elem == 0:
            break
        try:
            if heap[elem] >= heap[(elem-1)//2]:
                heap[elem], heap[(elem-1)//2] = heap[(elem-1)//2], heap[elem]
                elem = (elem-1)//2
            else:
                break
        except:
            break
            
def heapDelete():
    global heap
    if len(heap) == 0:
        return 0
    root = heap[0]
    heap[0] = heap[-1]
    heap.pop()
    elem = 0
    while True:
        left = 2 * elem + 1
        right = 2 * elem + 2
        largest = elem
        # 왼쪽 자식이 존재하고, 자식이 부모보다 크다면
        if left < len(heap) and heap[left] > heap[largest]:
            largest = left
        # 오른쪽 ''
        if right < len(heap) and heap[right] > heap[largest]:
            largest = right
        if largest == elem:
            break
        heap[elem], heap[largest] = heap[largest], heap[elem]
        elem = largest
    return root


result = []
for _ in range(N):
    command = int(sys.stdin.readline())
    if command == 0:
        print(heapDelete())
    else:
        heapAdd(command)

-> 백준 1655번 답안

오답노트

개선 전

newRoot = heap.pop()
heap.reverse()
deleted = heap.pop()
heap.append(newRoot)
heap.reverse()

힙 요소 제거 함수의 루트를 빼내는 작업을 처음에 이런식으로 구현했었다. deque모듈을 쓰지 않았으니 빼고, 뒤집고, 빼고 하는 작업이 일반적인 리스트 연산보다 빠를 거라고 생각했다. 아니나 다를까 시간초과.. 이후 서칭을 통해 더 좋은 방법을 발견했고, 이를 적용하니 무사히 통과할 수 있었다.

개선 후

root = heap[0]
heap[0] = heap[-1]
heap.pop()
elem = 0