[PG_LV2] 멀쩡한 사각형

• 최대공약수를 구한다.
• 문제에서 발생하는 패턴에 대해 이해한다.
  

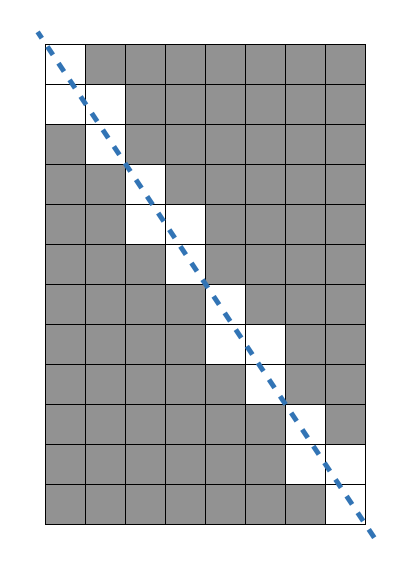
특정 사각형이 있을 때, 양 옆 꼭지점을 기준으로 반을 잘랐을 때, 1cm x 1cm의 정사각형으로 온전히 자를 수 있는 부분의 넓이가 얼마냐는 문제이다.

🍕 내가 푼 답

온전한 부분의 넓이을 구하기 위해서,
온전하지 않는 부분의 넓이을 구해서 전체 넓이에서 빼야하는데

온전하지 못한 부분 = (가로 + 세로 - 최대공약수);

답은 가로 * 세로 - ( 가로 + 세로 - 최대공약수);

    private long Sample()
    {
        long count = GCD(w, h);
        long all = (long) w * h;
        
        return all - (w + h - count);

    }

// a > b라는 가정 하에, a % b 나머지가 0이 아니면, 
// 나머지가 0이 될때 까지, b을 나머지로 나누면 최대공약수가 나온다.
    private int GCD(int a, int b)
    {
        if (a < b)
        {
            int temp = b;
            b = a;
            a = temp;
        }
        if (a % b == 0)
        {
            return b;
        }

        return GCD(b, a % b);
    }

🍔 다른 사람이 푼 답

BigInteger 라이브러리을 이용해서 간단하게 풀었다.
gcd도 따로 만들 필요 없이 제공된다.

import java.math.BigInteger;

public class Solution 
{

    public long solution(int w, int h) 
    {
        long totalCount = (long) w * (long) h;
        long diagonalCount = w + h - BigInteger.valueOf(w).gcd(BigInteger.valueOf(h)).longValue();

        return totalCount - diagonalCount;
    }
}