(출처) https://algospot.com/judge/problem/read/DICTIONARY
그래프 만들기
먼저 들어오는 알파벳 단어의 첫 글자는 이어서 들어오는 다음 글자들에 비해 우선권을 갖는다. 만약 단어의 첫 글자가 같다면 우선권 판단은 다음 글자로 넘어간다.
해당 속성을 이용하여 모든 알파벳 단어 26글자를 하나의 정점으로 바라보고, 우선된 글자를 기준으로 방향을 이어 간선을 연결하면 사이클이 없는 방향그래프가 만들어진다.
해당 문제에서 요구하는 것은 26개의 알파벳들의 우선순위(의존성)를 비교하여 순서대로 줄을 세우라는 것인데, 사이클이 없는 방향그래프의 경우 깊이우선탐색으로 그래프들의 정점들을 방문하기만 하더라도 문제에서 요구하는 우선순위 순서별로 올바르게 모든 정점을 탐색할 수 있다. (위상정렬)
(깊이우선탐색은 현재 연결된 간선 중 방문하지 않은 곳을 택해 막다른 곳까지 계속해서 탐색하는 그래프의 탐색기법 중 하나이다)
이때 그래프를 만들기 위해서는 입력으로 주어지는 단어 N 개를 모두 비교해 봐야한다. 들어올 수 있는 개별단어의 최대길이 M이라고 했을 때, 그래프를 만드는 데는 O(N * M)의 시간복잡도가 소요된다.
이때 N의 최댓값은 200, M은 20이므로 그래프를 만드는 것에서 시간복잡도의 제한은 신경 쓰지 않아도 된다.
DFS 탐색
입력으로 주어지는 단어들로 모든 알파벳(정점)의 우선순위가 정해진다는 보장은 없다. 서로 연결되지 않아 구역이 나눠진 점들이 여러 개 생길 수도 있다는 것.
따라서 총 26개의 정점들을 각각 시작점으로 삼아 1번씩은 모두 탐색을 진행해 보아야 한다.
(탐색을 한다는 것은 방문한다는 것이 아니라 우선은 방문을 할지, 하지 않을지 검사하고 아직 방문되지 않는 점이었을 경우에만 방문으로 이어지는 로직을 말하는 것으로, 이것을 모든 점에 모두 1번씩은 돌려주어야 한다는 것)
나는 그래프를 벡터배열을 이용하여 구현했는데 총 26개의 정점(알파벳)과, 모든 정점을 1번씩은 탐색해 주기 위하여 모든 점과 간선이 연결되어 있는 시작점을 추가로 넣어줬다.
시간복잡도는 총 N(26)번의 탐색로직, 그리고 각 1번의 탐색은 시작점과 연결된 간선을 모두 확인하는 작업으로 이어지므로 결국 O(N + E) 인데, 모든 정점이 전부 연결되어 있는 최악의 경우를 생각해 보아도 O(N^2)이 되므로 해당 문제에서는 최대 676번의 계산이 필요하게 된다. 시간제한은 절대로 걱정할 필요는 없다.
코드
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
using namespace std;
const string INVALID = "INVALID HYPOTHESIS";
vector<vector<int>> graph(27, vector<int>());
string ret = "";
// a=1,b=2,...,z=26
int ascii(char alphabet) {
int ret = (int)alphabet - 96;
return ret;
}
string ascii(int alphabet) {
char ret_char = alphabet + 96;
string ret_string;
ret_string += ret_char;
return ret_string;
}
void connect_edge(char a, char b) {
graph[ascii(a)].push_back(ascii(b));
}
bool dictionary(vector<bool> &visited, vector<bool> &is_running, int vertax) {
is_running[vertax] = true;
visited[vertax] = true;
for (int i = 0; i < graph[vertax].size(); i++) {
int next = graph[vertax][i];
if (!visited[next]) {
bool is_valid = dictionary(visited, is_running, next);
if (!is_valid) return false;
}
else {
if (is_running[next]) return false;
}
}
is_running[vertax] = false;
if (vertax == 0) return true;
ret = ascii(vertax) + ret;
return true;
}
int main() {
int testcase;
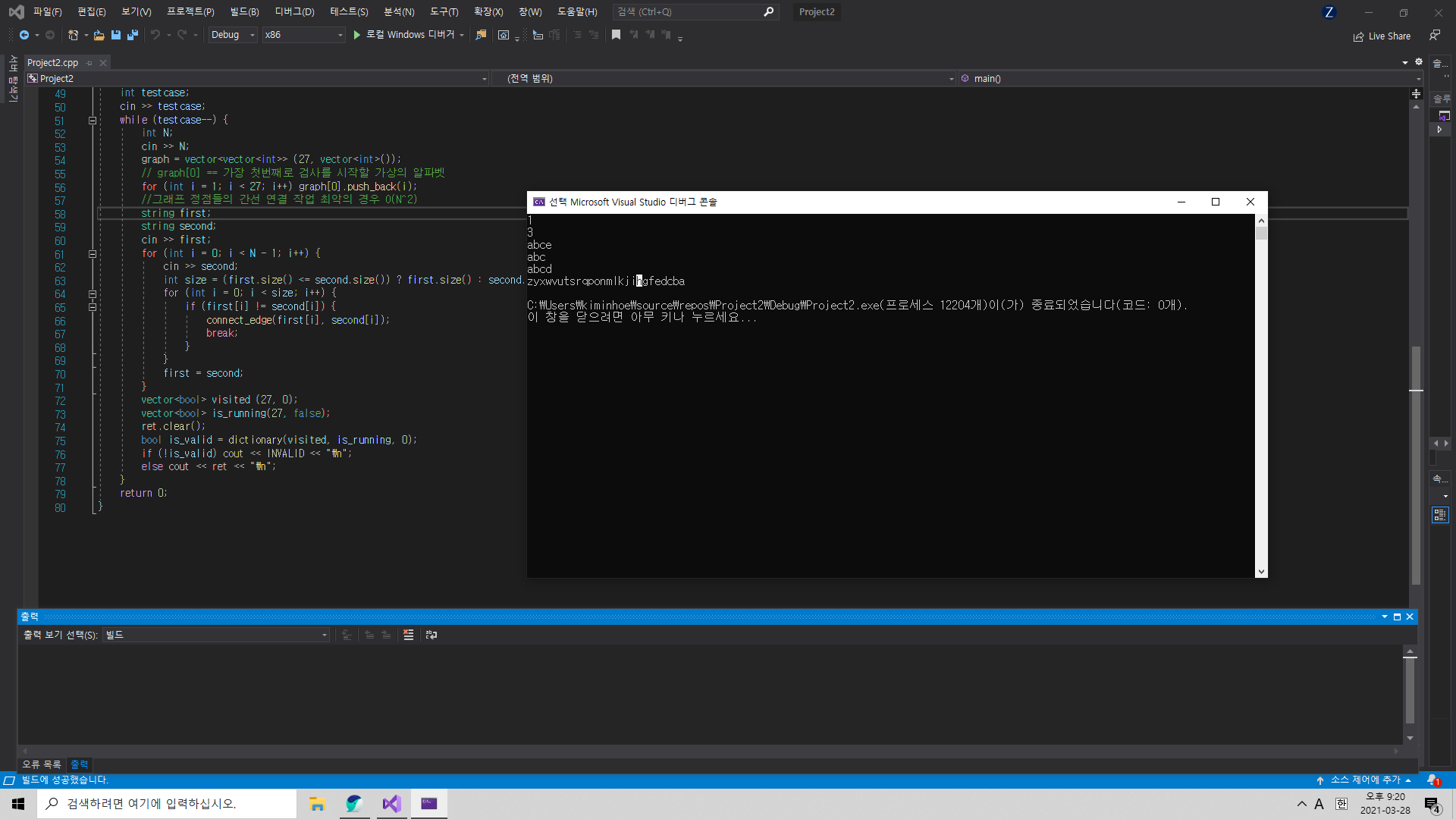
cin >> testcase;
while (testcase--) {
int N;
cin >> N;
graph = vector<vector<int>> (27, vector<int>());
// graph[0] == 가장 첫번째로 검사를 시작할 가상의 알파벳
for (int i = 1; i < 27; i++) graph[0].push_back(i);
//그래프 정점들의 간선 연결 작업 최악의 경우 O(N^2)
string first;
string second;
cin >> first;
for (int i = 0; i < N - 1; i++) {
cin >> second;
int size = (first.size() <= second.size()) ? first.size() : second.size();
for (int i = 0; i < size; i++) {
if (first[i] != second[i]) {
connect_edge(first[i], second[i]);
break;
}
}
first = second;
}
vector<bool> visited (27, 0);
vector<bool> is_running(27, false);
ret.clear();
bool is_valid = dictionary(visited, is_running, 0);
if (!is_valid) cout << INVALID << "\n";
else cout << ret << "\n";
}
return 0;
}기억하고 싶은 점
나는 구현의 편리성과 메모리의 효율을 생각해 입력을 한 번에 받는 방법을 택하지 않았다. 즉 들어오는 단어들을 모두 저장해놓고 한 번에 그래프를 만드는 것이 아니라, 2개씩 단어를 끊어서 입력을 받으면서 그래프를 만드는 방법을 택했다.
2개씩 끊어서 입력을 받으면 2개의 단어를 담을 메모리만을 가지고도, 해당 메모리를 계속 재활용하면서 모든 단어를 다 확인해 볼 수 있기 때문에 효율적이라고 생각했다.
책의 구현을 보니 나와 같은 방식을 이용한 것을 볼 수 있었다. 그런데 문제에 달려있는 댓글들을 읽어보다가 위 방식이 오류가 생길 여지가 있는 구현이었다는 것을 알게 되었다.
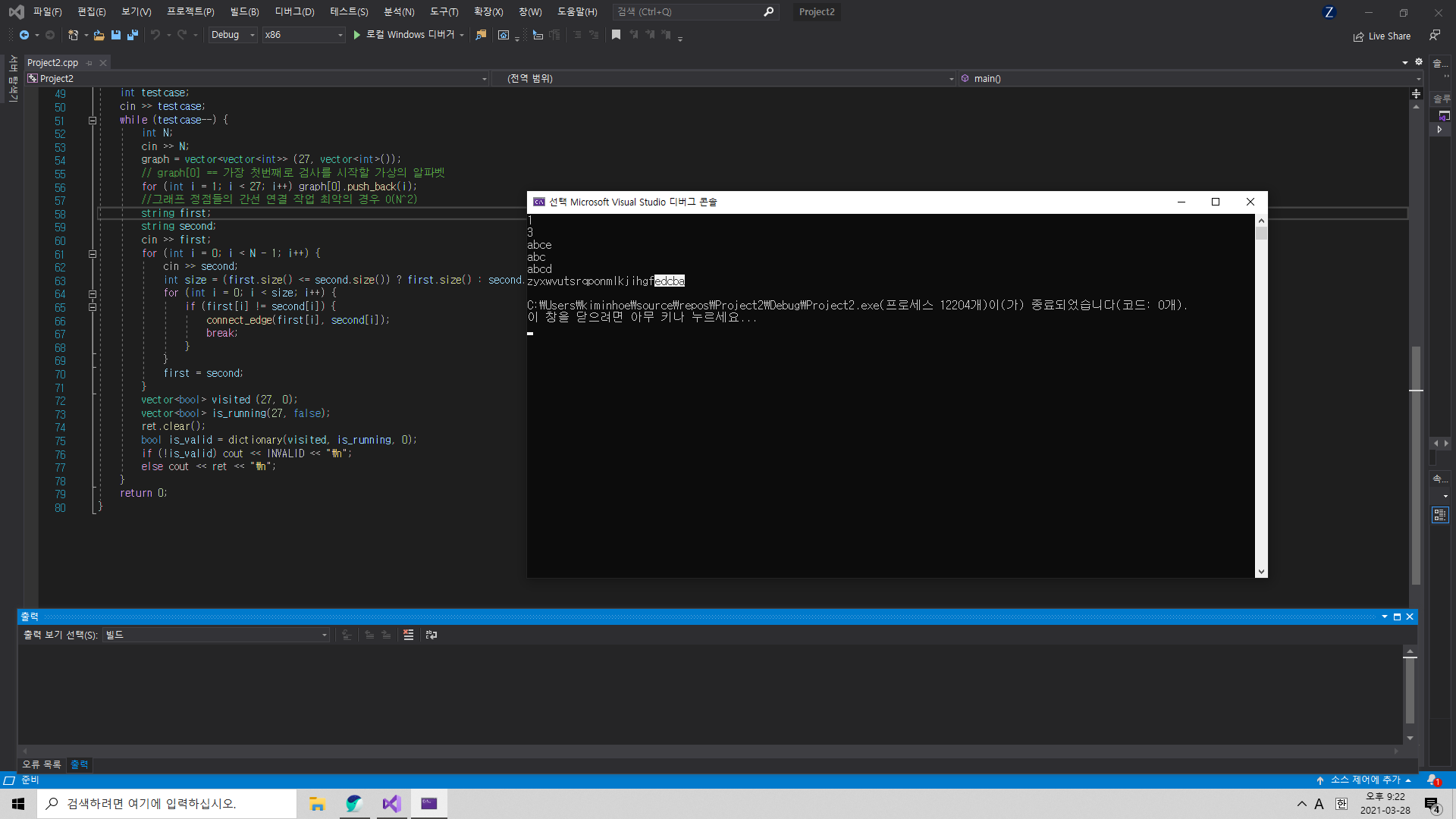
입력으로 들어오는 모든 단어들의 길이가 전부 같았다면 사실 위 구현도 문제가 될 것은 없었다. 하지만 만약 그림과 같이 글자수가 다른 입력단어가 들어오게 된다면, 단어를 2개씩만 검사하는 로직의 특성상 첫 번째 단어와 세 번째 단어의 연결관계검사가 진행되지 않는다.
결국 e는 d와의 우선관계순서를 정하지 않고 생략돼 버리는 문제가 발생한다. 즉 만들어지는 그래프는 실제와 다르게 e->d로 가는 간선이 존재하지 않아 제대로 답을 내놓지 않게 된다.
그냥 모든 단어를 배열에 전부 저장하고 빈칸은 공백칸으로 두어 단어들의 글자수를 일괄적으로 맞춘 뒤, N개의 단어를 한 글자씩(한 길이씩) 모두 확인하는 것이 확실히 안정적인 구현일 것 같다.
길이가 짧은 단어에 공백을 넣어주어 모든 단어의 글자수를 일괄적으로 맞춰준다면, 후에 각 단어의 글자 검사를 진행할 때 생길 수 있는 귀찮은 인덱스 오류를 미연에 방지하면서 더욱 쉬운 구현을 가능하게 할 것 같다.