HashTable

unodered_map (c++의 HashTable)

얼마전 알고리즘 문제를 풀면서 HashTable을 구현한 C++의 unodered_map 라이브러리를 사용해 보았다.

사실 HashTable의 필요성을 느낄만한 문제를 여지껏 별로 풀어본 적이 없었는데, 한번 사용해 보니 확실히 구현이 빡센 문제에서 유용하게 사용할 수 있을 것 같더라.

그리고 HashTable이라고 하면 대충 Hashing 전략을 이용한 효율적인 키 검색 라이브러리 비스무리 한 것이라고 어렴풋이만 알고만 있었지, 정확하게 제대로 공부하고 넘어간 적이 없었다는 생각이 문득 들었다.

그래서 HashTable에 대해서 한번 간단하게라도 공부하고 내용을 남겨보기로 하였다.

해싱(Hasing)

HashTable의 구동로직은 심플하지만 강력하다. 배열에 원하는 값을 저장한 다음 알맞게 꺼내 쓰는 것이 바로 HashTable의 구동로직이다.

물론 알맞게 값을 저장하고 또 저장한 값을 올바르게 꺼내 쓰기 위해서 약간의 처리 공정이 필요하다. 바로 Hasing이라는 공정이다.

Hasing은 검색에 이용될 Key값을 저장할 배열의 정수 인덱스와 알맞게 매칭해주는 과정, 즉 일련의 인덱싱 과정이라 생각하면 된다.

(Key값은 완성된 HashTable에서 자료를 검색할 때 사용할 Keyword라고 생각하면 편하다)

(물론 Hashing 과정에 어떠한 Hash함수를 쓰느냐에 따라서 MD5나 SHA와 같은 암호화 Hash값, 즉 문자열값을 내뱉을 수도 있다. 하지만 자료구조의 HashTable에서 말하는 Hashing의 결과물은 일반적으로 배열의 인덱스, 즉 인트 정수값이라고 간단하게 생각해도 될 것 같다)

(Hash 함수는 크게 암호학적, 비암호학적으로 함수로 나눠지게된다.
암호학적 Hash - MD5,SHA // 비암호학적 Hash - CRC32)

Key값을 Hasing하여 저장할 배열의 인덱스 값으로 변환한다.

이후 해당하는 배열의 인덱스 위치로 접근하여 벨류값을 넣어준다.

이것으로 HashTable을 모두 완성한 것이다.

완성된 HashTable에서 원하는 내용물을 꺼내고 싶을 때는, 다시 KEY를 Hasing하여 인덱스를 구하고 해당 인덱스로 배열에(HashTable) 접근하여 꺼내어 쓰면 된다. 굉장히 간단한다.

HashTable에서 자료를 꺼내 쓰는 과정은 결국 인덱스를 통한 배열의 임의접근 방식이므로, 정상적인 상황이라면 O(1)이라는 시간으로 원하는 자료에 접근할 수 있다. (최악의 경우 O(N)이 소모될 수 있다)

추가적으로 이 Key라는 값에는 문자열이 사용될 수도 있고, 객체 형태의 바이트 배열이 들어올 수도 있으며, 여러 가지로 다양한 형태의 자료형이 주어질 수가 있다.

따라서 Hashing에는 불특정 자료형의 Key를 인덱싱하기 편한 형태로 정제하는 과정이 우선적으로 필요하다. (일반적으로 정수형태로 정제한 후 인덱싱을 진행)

해시함수(Hash Function)

주어진 다양한 형태의 Key를 배열의 정수 인덱스로 알맞게 변환시키는 알고리즘 그 자체를 뜻한다.

주어진 Key를 우선 정수 형태로 정제한 뒤, 다시 해당 정수를 더 적은 범위로 압축시켜 최종적으로 배열 인덱스 정수로 변환시키는 과정을 바로 해시함수가 수행한다.

위에서도 언급했듯이 Key값에는 여러 가지 형태의 데이터가 들어올 수 있으므로, 인덱싱을 편하게 진행하기 위해서는 데이터별로 특정한 규칙을 정해 우선은 정수 형태로 변환시켜줘야 한다.

(예를 들어 Key로 "banana" 라는 문자열이 들어왔다고 하면, banana의 각 문자를 a=0~z=25 와 같이 정수로 치환한 뒤, 단어들의 위치 자리만큼 (26^자리수)을 곱하여 더한다면(26진수) 문자열을 정수로 치환하는 과정을 만들 수 있다)

그리고 이후 인덱싱을 진행한다.

(인덱싱의 경우 모듈러 연산을 통한 계산법을 대표적인 예시로 많이 든다. 만약 현재 내가 가진 HashTable 배열의 공간이 30개라면, 정제된 Key 값을 30으로 나눈 나머지를 해당 Key의 인덱스 값으로 쓴다)

결국 해시함수의 과정은 key값 정제 과정 -> 이후 인덱싱 과정으로 나눠진다고 볼 수 있을 것 같다.

해시충돌(Hash Collision)

HashTable에 들어올 수 있는 key의 개수는 사실상 무한이지만, 저장공간인 HashTable 배열을 무한으로 준비하는 건 당연하게도 불가능하다.

아무리 1인 1실이 원칙이라고 하더라도 한정된 공간에 무한한 입력을 쏟아 박으면 결국엔 원칙을 어기고 2인 이상이 들어가 버리는 공간이 생기게 된다.

Hasing을 진행하다 보면 서로 다른 Key이지만 같은 배열의 인덱스를 가리키는(같은 Hash값을 가리키는) 경우가 발생하게 된다는 것이다.

이러한 상황을 해시충돌이라고 부른다.

특정 Key를 Hasing 한 뒤 해당하는 인덱스에 값을 저장하려고 HashTable 배열을 찾아갔지만, 해시충돌로 인하여 이미 해당 공간을 다른 Key가 점유하고 있는 상황이 발생하곤 한다.

이와 같은 상황을 해결하는 방법에는 크게 2가지로 나누어진다.

바로 Open Address 방식과 Separate Chaining 방식이다.

Open Address 방식

Open Address 방식은 만약 저장해야 할 공간이 이미 점유 중일때, 배열의 다른 비어있는 공간을 찾아서 저장하는 방식이다.

비어있는 공간을 찾는 방법(탐사법)에도 여러 유형이 존재하는데, 대표적으로 Linear Probing, Quadratic Probing, Double Hashing과 같은 탐사법들이 존재한다.

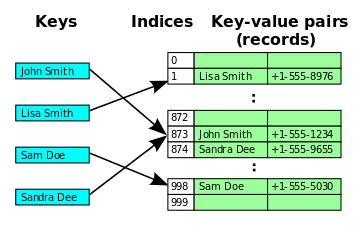
Open Address 방식은 HashTable에서 자료를 삭제하는 동작에 비효율적인 측면이 존재한다는 단점이 있다.

예를 들어, 그림에서 Sandra Dee는 Hash 인덱스 값이 873번이지만 해시충돌로 인하여 874번 인덱스로 이동되었다.

그런데 만약 873번의 "John Smith"라는 Key와 그 벨류값을 삭제시켜버리면, 해시충돌로 인해 다른 자리로 옮겨진 Sandra Dee는 그 위치가 모호해지게 된다.

왜냐하면 기존에는 "Sandra Dee" Key를 검색하는 경우, 먼저 873번에 도착하여 "John Smith"라는 Key를 먼저 확인하고 원하는 자료가 아님을 깨달은 뒤 다시 874번으로 이동하는 과정이 존재했다.

하지만 "John Smith" Key가 삭제되어 버린다면 이 873번 자리는 빈자리로 변할 것이고, 따라서 "Sandra Dee" Key를 검색하였을 때 873번 자리가 비어있으니 해당 Key 는 HashTable에 저장되어 있지 않는 키라고 받아들일 가능성이 생겨버린다.

874번 자리에 멀쩡히 자료가 저장되어 있지만 말이다.

이러한 문제점으로 인해 Open Address 방식에서 데이터를 삭제할 경우, 해당 자리를 완벽하게 제거하어 비워두는 것이 아니라 더미 데이터를 남겨두는 식으로 연결점을 남겨놓아야 한다.

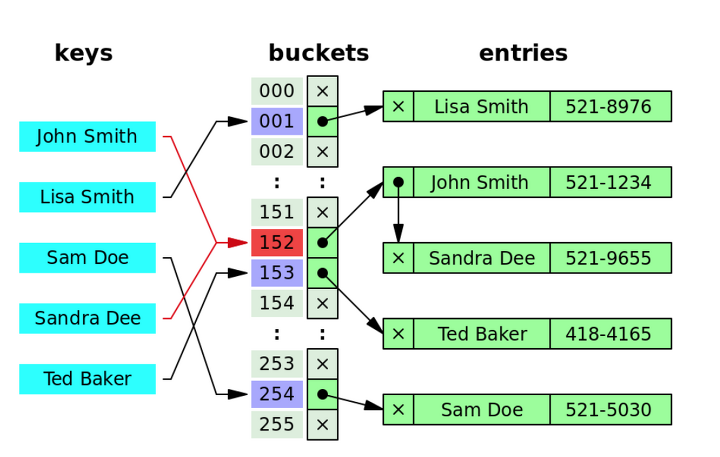
Separate Chaining 방식

Chaining 방식은 HashTable 배열의 저장공간에 또 다른 배열(정확하게는 연결리스트 혹은 이진탐색트리)을 두는 방식으로 해시충돌을 해결한다.

HashTable이 또 다른 배열들의 포인터를 보관하고 있는 포인터배열로 구성된다고 생각하면 편하다.

Open Address 방식과는 다르게 하나의 인덱스에 서로 다른 Key 값들을 다중으로 보관할 수 있는 구조이다.

이러한 Chaining 방식은 충돌이 일어난 데이터의 개수가 적을 때는 연결리스트에 보관하고, 데이터의 개수가 많아지면 이진탐색트리에 보관하는 식으로 구현한다고 한다.
(데이터의 개수가 많을 때는 이진검색을 이용해 효율적으로 데이터를 찾겠다는 뜻인 듯함)