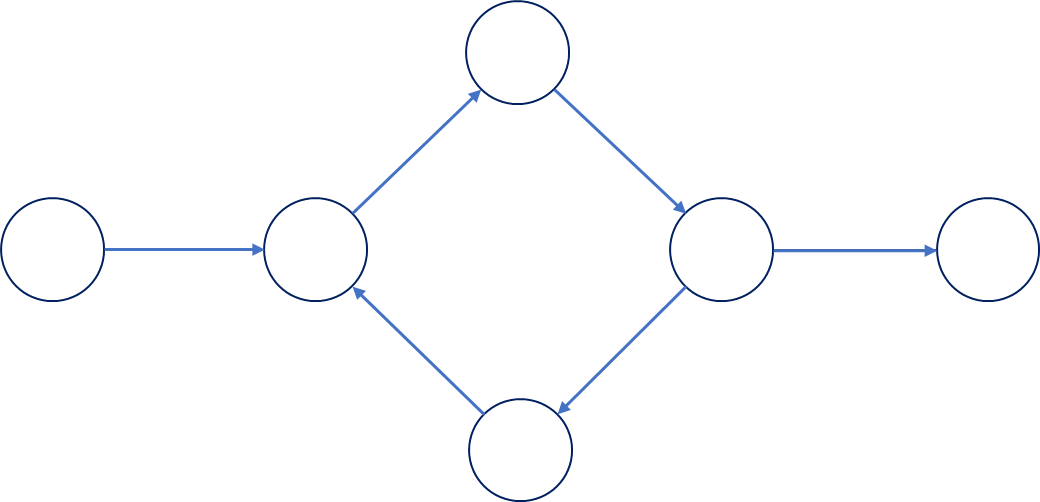
그래프 자료구조
노드(Node)와 엣지(Edge)로 이뤄져 각 노드들이 연결되어 시각적으로 나타낼 수 있으며, 해당 노드 간의 관계를 설명하는 자료구조.
일반적인 노드간의 관계 파악으로 SNS 관계도 및 도로상의 차량정보를 바탕으로 한 운송서비스나 기타 경로 파악에도 사용되며, 공간데이터를 활용해 상권파악이나 기타 등등의 다양한 산업에서 적용할 수 있다고 한다.
그래프 종류
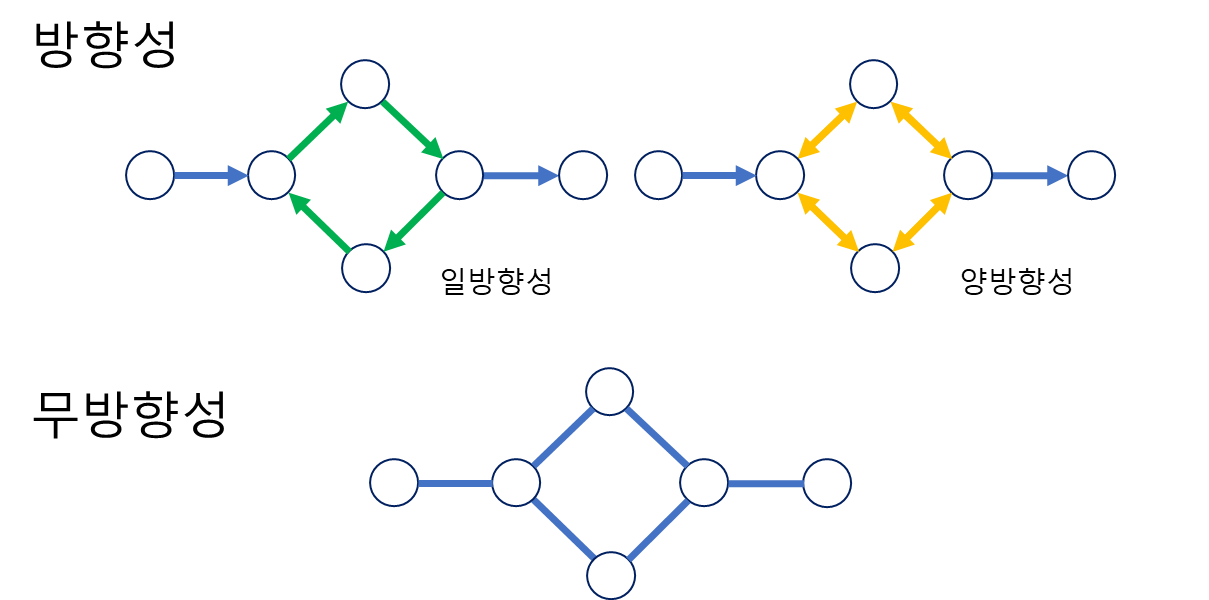
방향성(Directed)/무방향성(Undirected)
그래프 엣지의 방향으로 종류를 나누는 방법
방향성: 첫노드부터 끝노드까지 일련의 일관된 방향이 있는 경우 방향성으로 판단하며, 내부의 노드간 순환의 방향이 한쪽으로 '순환'하는지, 양쪽으로 순환하는지에 따라 일방향성과 양방향성으로 나뉜다.
* 순환에 대해선 아래에서 다뤄볼 예정이다
무방향성: 노드 간 연결이 따로 방향성을 띄지않고(화살표 없음) 연결되어있는 모든 노드가 서로 상호관계를 갖는다.
순환 Cyclic / 비순환 Acyclic 그래프
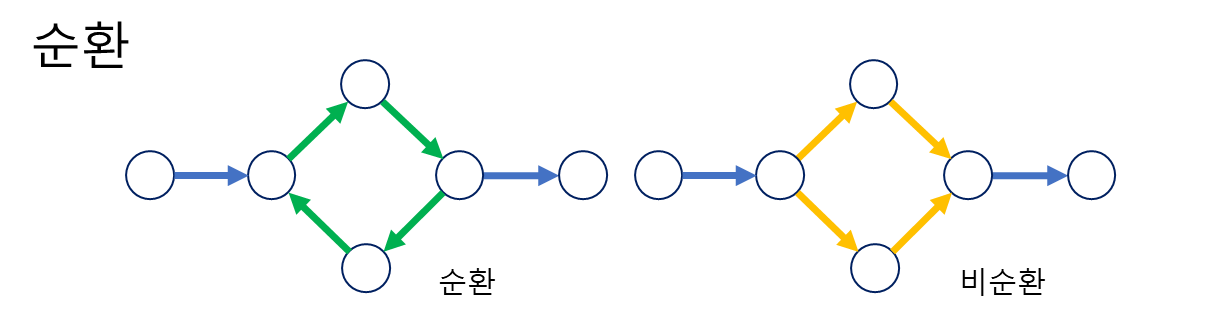
순환의 여부로 그래프를 분류하는 방법
* 기본적으로 무방향성은 모든 엣지가 양방향을 취하므로 순환그래프에 속한다.
순환: 내부에서 방문했던 노드를 다시 방문하게 되는 경우가 발생
비순환: 내부에서 재방문이 진행 안되는 방향으로 구성됨
가중 (Weight) 그래프
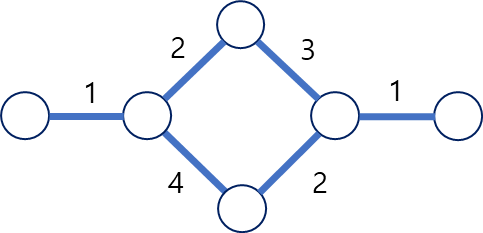
각각의 엣지에 가중치가 있는 형태. 일반적으로 가중 그래프가 아닌 경우는 가중치를 1로 생각하면 되며, 가중 그래프와 같이 각각의 엣지에 가중치가 있는 경우, 해당 가중치를 최대/최소화 하는 결과를 내는 경로를 탐색한다.
- 가중치를 직접 정하고 그에 따른 의사 결정을 하도록 해야한다.
대개의 경로분석은 총 가중치가 가장 낮은 경우를 파악한다.
그래프의 활용방법
그래프를 자료구조로써 이용하기 위해 활용하는 방법은 대표적으로 인접행렬과 인접리스트가 있다. 각각의 방식에 특징이 있으며, 장단점이 있으니 적재적소에 알맞게 활용하면 좋다.
인접 행렬(Adjacency matrix)
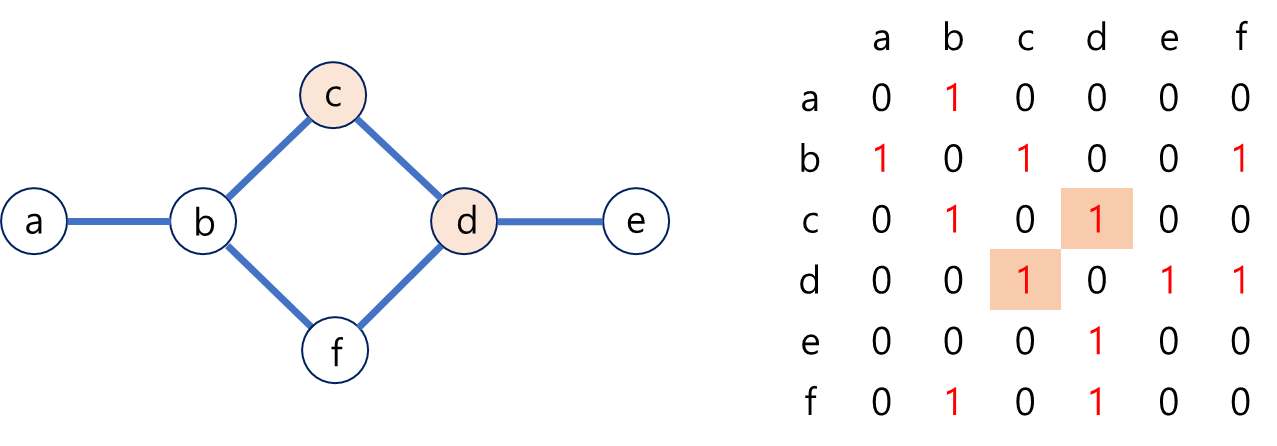
무방향 그래프인 왼쪽과 같은 관계를 가진 그래프 자료구조를 행렬 형태로 나타낸 것이 오른쪽과 같다.
각각의 정점(인접한 노드)의 엣지가 있을 경우 이를 표시하는 방법이며, 자기 자신은 0으로 두어 대각 행렬은 항상 0으로 유지한다.
해당 그래프 이미지에서의 C와 D의 관계를 파악해보면 오른쪽의 인접행렬과 같이 표시할 수 있다.
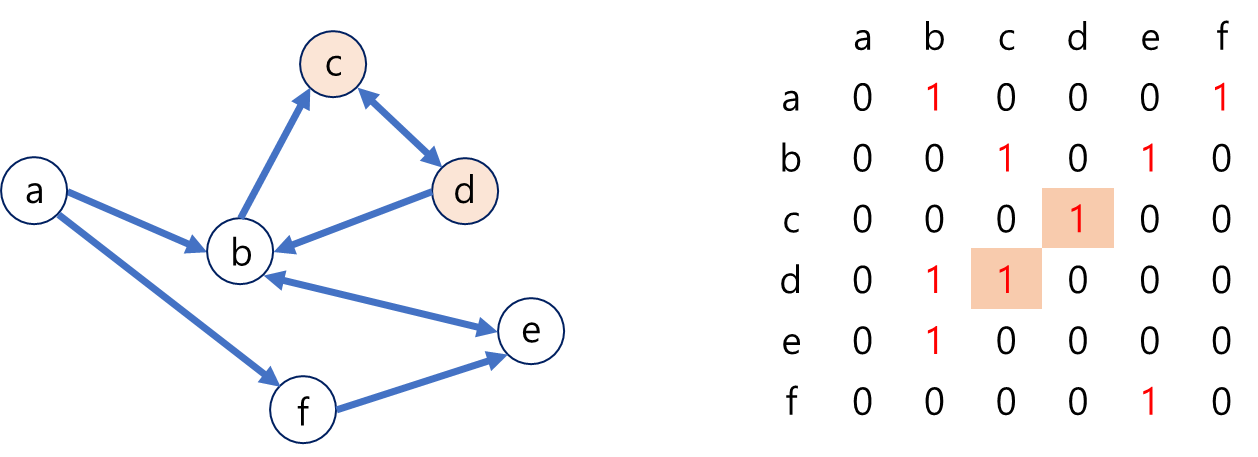
위에서와 달리 양방향 순환 그래프의 인접 행렬은 오른쪽과 같이 표현할 수 있다.
무방향에서는 엣지로 연결된 두 노드가 모두 상호작용하므로 행과 열이 서로 대칭되어있는 반면, 방향이 있는 그래프에서는 대칭되지 않는다.
-
Memory 사용이 많다. 엣지가 많다면 그만큼 효율적으로 사용할 수 있지만, 노드 수 대비 엣지가 적은 희소 그래프의 경우 인접 행렬 자체가 희소 행렬이 되어 비효율적으로 메모리 공간을 잡아먹게 된다.
-
노드의 위치를 행렬상으로 파악하고 있기 때문에 탐색의 시간복잡도가 으로 빠른 편이다.
코드 상에서는 matrix 상에서 a,b,c 등 노드의 index가 보이지 않아 이를 파악할 다른 장치를 활용하는 등의 방법을 취해야 한다. -
탐색과 달리 노드의 연관성 있는 노드를 모두 찾거나, 연결된 노드에 특정 액션을 취하는 것은 전체 노드를 탐지해서 인접노드를 찾아야 하므로 시간복잡도가 이 된다.
-
1이 아니 추가적인 숫자를 이용해 엣지의 가중치를 조절하기 편리하고, 구현 자체가 쉽다.
인접리스트(Adjacency List)
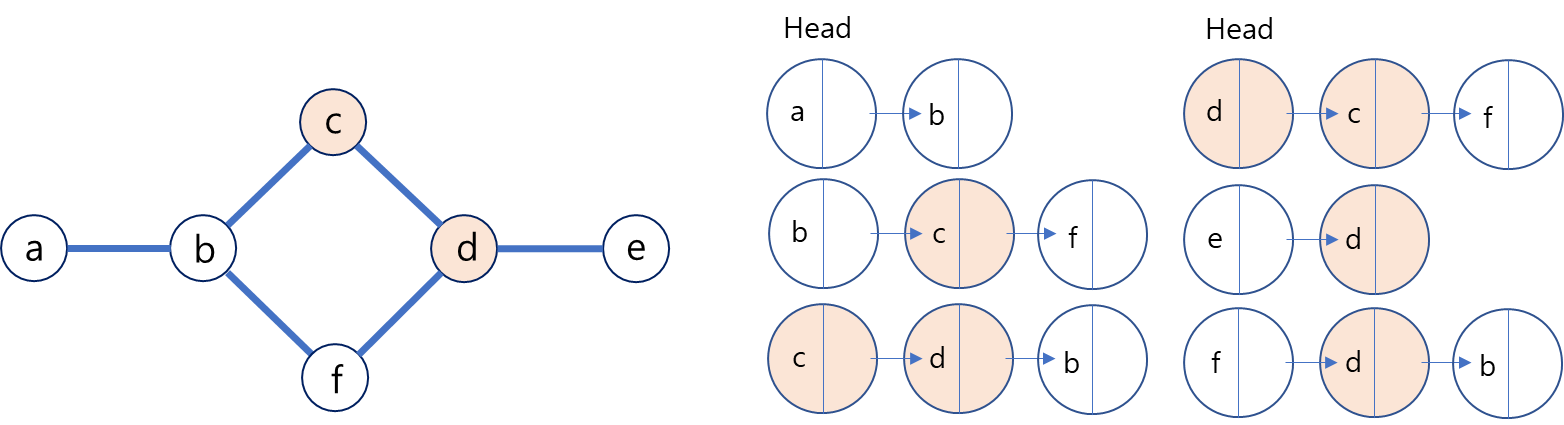
인접리스트는 그래프의 노드 간 연결 된 엣지를 바탕으로 관계를 파악해 연결리스트로 연결하는 방식을 취한다. 이미지와 같이 각각의 노드의 입장에서 연결된 노드를 연결리스트로 연결한다.
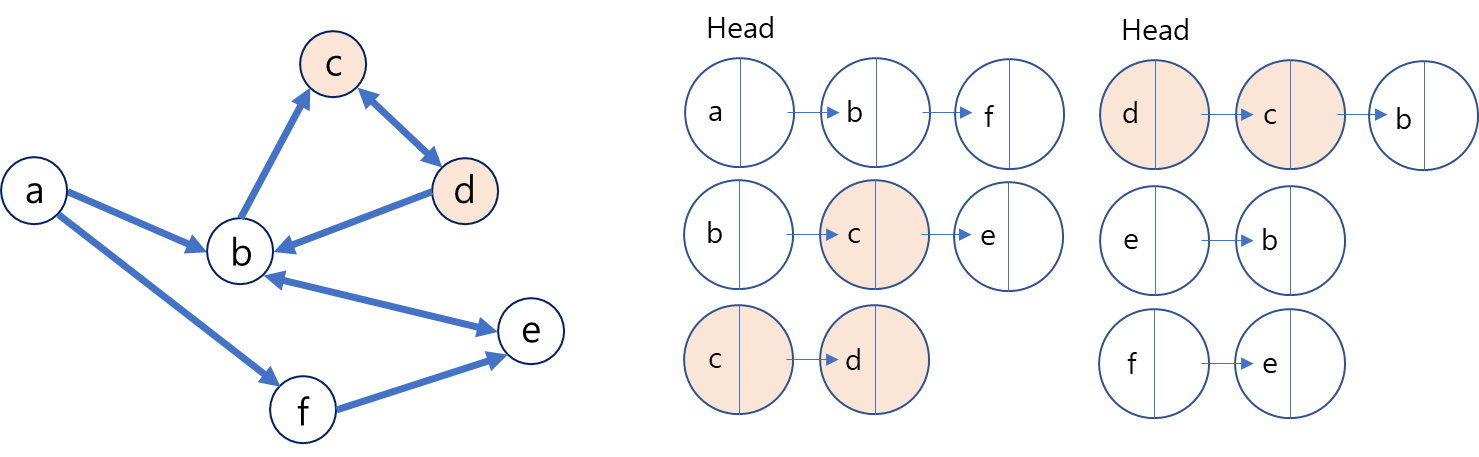
- Memory의 사용이 인접 행렬에 비해 상대적으로 적은 편이다. 필요한 엣지의 개수 만큼만을 사용하기 때문
- 특정 노드에 대한 어떠한 액션을 취하는 것은 해당 인접노드 내만 찾아보면 되므로 로 볼 수 있다.
그래프의 순회
그래프 및 트리 구조에서 노드를 한번씩 탐색하는 개념.
모든 또는 특정 노드를 방문하는 방법을 찾는 것으로 노드 간의 연결 사이에서 한번씩 방문하는 방법을 의미한다.
트리구조의 전위순회, 중위순회, 후위순회의 개념을 base로 한다.
* 트리구조는 그래프 중 방향성 비순회 그래프 - DAG(Directed Acycling Graph)에 속한다.
깊이 우선 탐색 - DFS(Depth First Search)
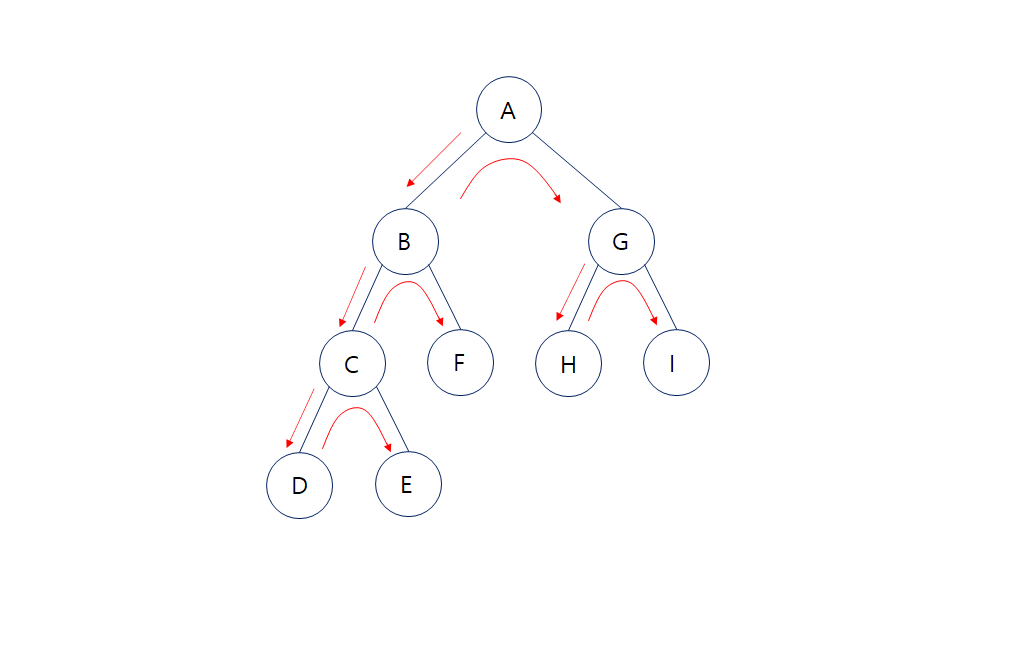
이름 그대로 깊게 먼저가면서 노드를 하나하나 방문하는 탐색 방식이다.
- 트리 그래프의 왼쪽부터 가면서 전위순회 순서로 진행 된다. (A-B-C-D-E-F-G-H-I 순)
- 루트노드 - 좌측노드 - 우측노드 순으로 더 깊은 계층을 우선 탐색하는 방식
- 재귀적인 방법을 사용해 시간이 오래 걸릴 순 있지만, 계층을 탐색한 뒤 재귀호출 하면서 저장된 메모리를 삭제하기 때문에 메모리적인 효율은 너비우선탐색보다 좋은 편이다.
재귀호출을 이용한 DFS 구현:
dfs_graph = { # 그래프를 인접리스트 딕셔너리로 표현
1: [2,3,4],
2: [1,5,6],
3: [1,6],
4: [1],
5: [6,7],
6: [5],
7: [6]
}
def dfs_recur(node, dfs_list= [] ): # 정한 노드로부터 탐색
dfs_list.append(node) # 인접노드 덧붙이기
for i in dfs_graph[node]: # 인접리스트의 해당 노드의 인접노드 파악
if i not in dfs_list: # 인접노드가 결과 리스트에 없으면
dfs_recur(i, dfs_list) # 재귀호출로 해당 노드의 인접 노드를 탐색
return dfs_list
dfs_recur(1)[output]
[1, 2, 5, 6, 7, 3, 4]인접리스트를 딕셔너리 자료구조를 이용해 작성했다.
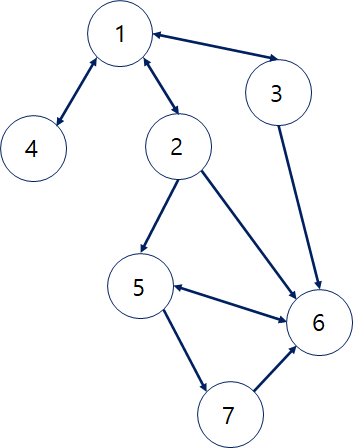
- 1번 노드를 먼저 결과 리스트에 넣고, 연결된 가장 첫번째 노드인 2번 노드를 탐색한다.
- 2번 노드에 연결된 가장 첫번째는 1번 노드인데, 이미 결과 리스트에 있으므로 5번 노드를 탐색
- 5번 노드를 결과 리스트에 넣고, 연결된 가장 첫번째 노드인 6번 노드를 향한다.
- 6번 노드는 5번과 연결되어있는데, 이미 결과 리스트에 들어있으므로 다시 이전 단계인 5번으로 되돌아간다.
- 이번엔 5번 노드의 두번 째로 연결된 7번 노드를 탐색
*위와 같은 방식을 반복해서 반복문이 종료될 때까지 진행한다.
STACK을 이용한 DFS 구현
dfs_graph = { # 그래프를 인접리스트 딕셔너리로 표현
1: [2,3,4],
2: [1,5,6],
3: [1,6],
4: [1],
5: [6,7],
6: [5],
7: [6]}
def dfs_stack(start_node):
visited = [] # 방문한 노드는 체크해서 피할 것
need_visited = [start_node] # 방문해야하는 노드를 체크할것. 시작노드로 초기화
while need_visited: # 방문해야하는 노드가 있으면 반복을 진행
node =need_visited.pop() # 방문해야하는 노드를 리스트의 맨 마지막 부분을 빼고 node 변수에 담기
if node not in visited: # 방문해야 하는 node가 방문한 리스트에 없다면
visited.append(node) # 방문 리스트에 넣어주고
need_visited.extend(dfs_graph[node]) # 방문 해야하는 리스트에는 다시금 방금 탐색한 노드의 인접노드를 넣기
return visited
dfs_stack(1)[output]
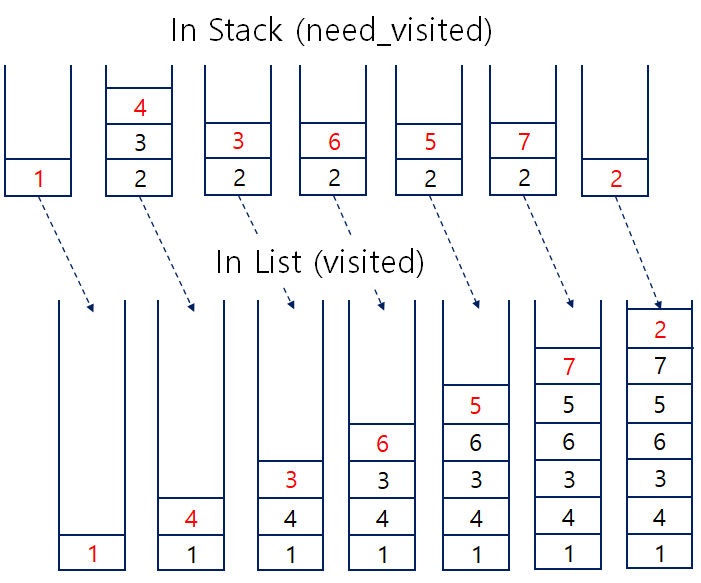
[1, 4, 3, 6, 5, 7, 2]DFS를 스택으로 구현하면 위와같이 작성할 수 있다.
- 반복문의 마지막 단에 extend를 통해 방금 방문한 노드의 인접노드를 방문 할 리스트에 넣는다.
- 다시 반복문의 첫 부분에서 Stack의 특성을 살려 pop()을 이용해 맨마지막 노드를 불러낸다.
* 이 부분이 헷갈릴 수 있는데, 이 작업을 반복했을 때 stack의 맨 안쪽에 남아있는 것은 가장 먼저 넣었던 노드의 인접 노드 중 하나가 될 것이다. 그만큼 더 깊은 계층까지 먼저 탐색하고 다시 돌아 오는 것을 상상해보면 이해가 된다. - 스택으로 구현 시 결과가 약간 달라지게 되는데, 인접리스트 내 인접노드의 원소 순서가 뒤바뀌기 때문이다. 이를 똑같이 하고 싶다면 원소의 삽입순서를 역으로 두면 된다.
- 재귀호출 방식보다 빠른 장점이 있다.
너비 우선 탐색 - BFS(Breadth First Search)
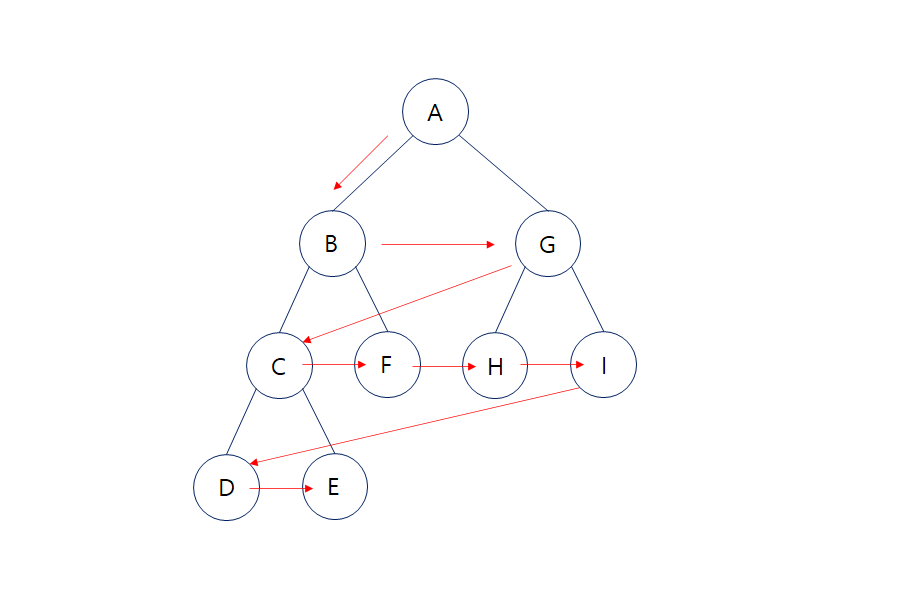
깊이우선탐색이 계층을 먼저 깊에 들어가서 탐색하는 순회 방법이었다면, 너비우선탐색은 같은 계층부터 먼저 탐색한 후, 각각의 계층의 노드에 인접한 노드를 탐색한다. 인접노드를 탐색할 때에도 다음 계층을 바로 들어가지 않고, 같은 계층의 다른 노드를 먼저 탐색한 뒤, 다음 계층으로 차근 차근 넘어가는 방법이다.
- 같은 계층의 노드 우선 탐색의 방법을 이용한다. (A-B-G-C-F-H-I-D-E 순)
- 루트노드 - 좌측노드 - 모든 형제노드 - 맨 처음 형제노드의 좌측노드 순으로 탐색 진행한다.
- 같은 계층을 먼저 탐색하다보니 형제노드들의 인접노드에 대한 정보들이 계속 Queue에 담겨있게 되어 메모리 효율이 떨어진다.
- 엣지 또는 데이터가 적은 경우 최단거리를 찾는데엔 효과적이다.
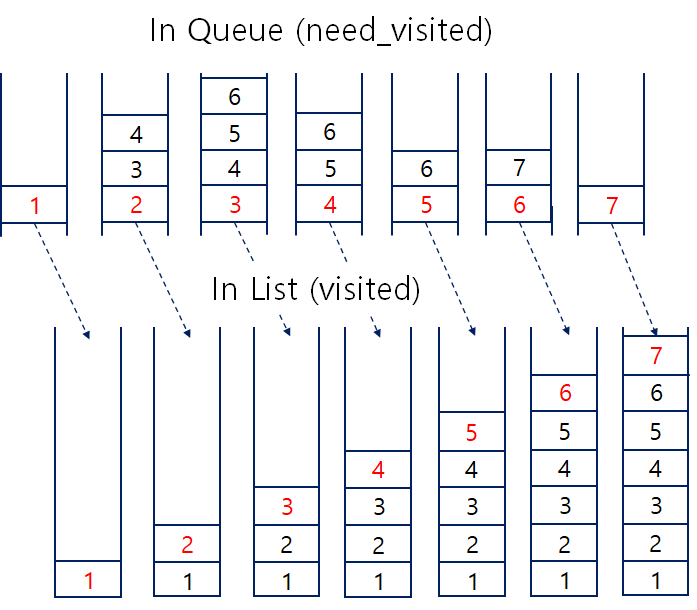
Queue를 이용한 BFS 구현
def bfs_queue(start_node):
visited = [] # 방문한 노드는 체크해서 피할 것
need_visited = [start_node] # 방문해야하는 노드를 체크할것. 시작노드로 초기화
while need_visited: # 방문해야하는 노드가 있으면 반복을 진행
node =need_visited.pop(0) # 방문해야하는 노드 리스트의 맨 앞 부분을 빼고 node 변수에 담기
if node not in visited: # 방문해야 하는 node가 방문한 리스트에 없다면
visited.append(node) # 방문 리스트에 넣어주고
need_visited.extend(dfs_graph[node]) # 방문 해야하는 리스트에는 다시금 방금 탐색한 노드의 인접노드를 넣기
return visited
bfs_graph = { # 그래프를 인접리스트 딕셔너리로 표현
1: [2,3,4],
2: [1,5,6],
3: [1,6],
4: [1],
5: [6,7],
6: [5],
7: [6]}
bfs_queue(1)[output]
[1, 2, 3, 4, 5, 6, 7]- DFS의 스택 방식에서 pop()을 해주는 위치만 맨 뒤 -> 앞으로 바꾸어 큐(queue) 구조로 진행한다.
- 그림과 같이 같은 계층의 형제 노드들의 자식노드를 미리 큐의 rear부분에 넣어둔 뒤, 앞쪽의 형제노드를 먼저 탐색해나가는 방식이다.
* 앞에서도 언급했지만, 이러한 이유로 데이터가 많은 경우는 쌓이는 인접노드 데이터(자식노드)가 많아져 메모리 효율이 떨어지게 된다.