Deep Learning - 딥러닝 이론 정리 2-2 (역전파, 체인룰, 가중치 업데이트, 경사하강법)

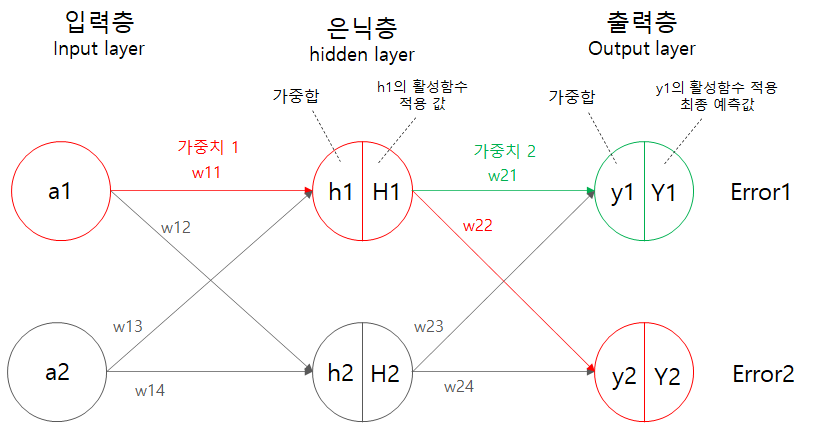
순전파

신경망의 순전파 진행의 순서는 아래와 같다.

• 입력값 전달
• 가중치 * 입력값 + 편향의 가중합을 은닉층에 전달
• 은닉층의 필요에 의해 활성화 함수 적용
• 다음 은닉층 또는 출력층의 노드에 대한 가중합을 전달
• 해당 노드에서의 활성화 함수 적용

위와 같이 입력층 > 출력층의 순서로 수많은 노드들에 대한 연산을 진행해 예측값을 출력하는 것이 신경망의 간략한 구조라고 할 수 있다.

오차 역전파(Propagation of Error)

신경망의 역전파는 출력층 > 입력층의 순으로 거꾸로 되짚어보면서 출력되었던 예측값 - 실제값의 차이(오차)를 최소화 할 수 있는 매개변수(가중치, 편향)을 찾아 업데이트 하기 위한 알고리즘이다.

역전파의 원리 $\frac {\delta Error}{\delta Weight}$

거꾸로 되짚어보면서 최적의 가중치를 찾는 방법은 무엇일까?
미분을 활용하는 방법으로, 이 전 레이어에서의 가중치에 대한 미분을 통해 가중치의 변화에 따라 얼마나 에러가 변하는지를 찾는 방법이다.

미분을 통해 가중치(Weight)의 변화에 따라 오차(Error)가 얼마나 변하는지를 파악해, 이를 최소화 할 수 있는 가중치(및 편향)을 찾는 것이다.

연쇄법칙(Chain Rule)을 이용한 가중치 업데이트

역전파는 미분을 이용해 출력층 > 입력층 방향으로 거슬러 올라가는데, 내부 은닉층의 가중치를 출력층에서 나온 오차에서 직접 미분할 수 없기 때문에 연쇄법칙을 이용해 목표 가중치까지 다가간다.

역전파 진행

$W_i = W_{i-1} - \eta\frac{\delta Error}{\delta W}$

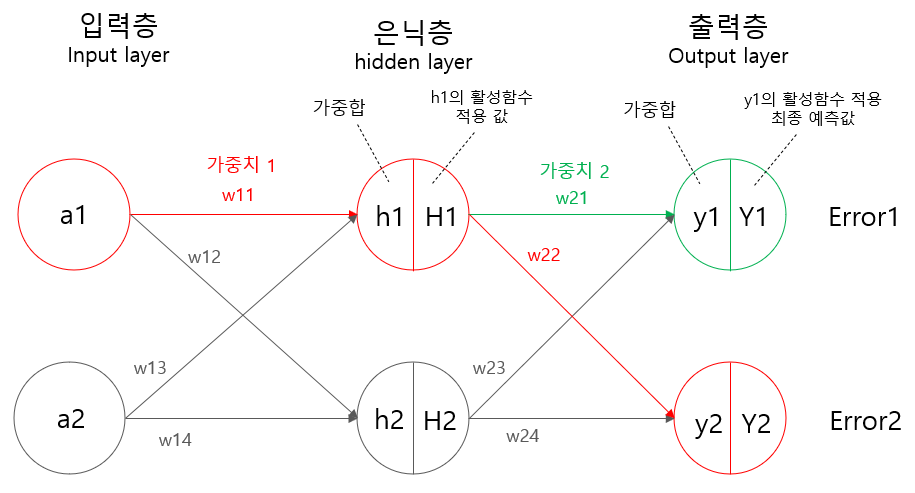
역전파를 통한 가중치를 업데이트 하는 공식은 위와 같다. 위의 수식을 이용해 가중치 업데이트 과정을 살펴본다.

가중치 w21 업데이트 진행은 위 그림의 초록색 부분의 작업이 된다.

해당 가중치의 업데이트를 식으로 나타내면 아래와 같다.

$𝑤21$(업데이트후)=$𝑤21$(업데이트전) - 학습률 * $\frac {\delta Error1}{\delta w21}$

가중치 $w21$를 구하는 것은 Error1의 $w21$에 대한 편미분값을 구하는 것인데, Error1는 중간에 다른 과정들이 있기 때문에 다이렉트로 $W21$를 미분할 수 없다. 그러므로 체인룰을 이용해서 Y1을 미분하고, Y1에서 y1을 미분한 뒤, 마지막으로 y1에서 w21을 미분해야 한다.

$\frac{\delta Error1}{\delta w21} = \frac{\delta Error1}{\delta Y1} * \frac{\delta Y1}{\delta y1} * \frac{\delta y1}{\delta w21}$

초록색 부분만의 계산을 통해서 $\frac {\delta Error1}{\delta w21}$를 구할 수 있고, 지정된 학습률 $\eta$를 곱한 뒤 이전 $w21$에서 빼주면 그 다음에 학습 될 $w21$를 업데이트 하게 된다.

가중치 1 w11의 업데이트는 위 그림 초록색과 빨간색으로 이뤄진다.

해당 가중치의 업데이트를 식으로 나타내면 아래와 같다.

$w11(업데이트후)=w11(업데이트전)-학습률 * (\frac{\delta Error1}{\delta W21}+\frac{\delta Error2}{\delta W21})$

w11의 경우 2개의 출력층에서 2개의 오차(Error1, Error2)를 받아야 하기 때문에 두 곳에서의 미분값을 구해 더해준다.

$\frac {\delta 𝐸𝑟𝑟𝑜𝑟1}{\delta 𝑤11}=(\frac {\delta 𝐸𝑟𝑟𝑜𝑟1}{\delta 𝑌1} ∗\frac {\delta 𝑌1}{\delta 𝑦1} ∗\frac{\delta 𝑦1}{\delta 𝑤21}) *\frac{\delta 𝑤21}{\delta 𝐻1} ∗\frac{\delta 𝐻1}{\delta ℎ1} ∗\frac{\delta ℎ1}{\delta 𝑤11}$

Error1을 모두 풀어내면 위와 같이 식을 세울 수 있는데, Error1부터 연쇄법칠을 통해 $w11$까지 미분을 진행한 것이다. 그 중 괄호로 표시된 부분은 기존 $w21$ 구할때와 같은 식인 것을 볼 수 있다.

$\frac {\delta Error2}{\delta w11} = \frac {\delta 𝐸𝑟𝑟𝑜𝑟2}{\delta 𝑌2} ∗ \frac {\delta 𝑌2}{\delta 𝑦2} * \frac {\delta 𝑦2}{\delta 𝑤22} ∗ \frac{\delta 𝑤22}{\delta 𝐻1} ∗\frac {\delta 𝐻1}{\delta ℎ1} ∗ \frac {\delta ℎ1}{\delta 𝑤11}$

Error2에서도 w11를 바로 미분하지 못하므로 연쇄법칙 이용한다. 이번엔 Error2에서 H1을 거치고 그 뒤는 Error1과 동일함을 알 수 있다.

이렇게 구해진 $\frac {\delta Error1}{\delta w11} + \frac {\delta Error2}{\delta w11}$에 지정된 학습량 $\eta$를 곱해 기존 $w11$에서 빼줌으로서 다음 번 학습때 진행하게 될 가중치가 결정이 되는 것이다.

역전파에서의 경사하강

역전파를 통해 가중치를 구하는 식은 $W_i = W_{i-1} - \eta\frac{\delta Error}{\delta W}$ 로 나타낸다.
위에서 가중치의 기울기($\frac{\delta Error}{\delta W}$)를 구한 뒤, $W_{i-1}$에서 빼주는 이유는 경사하강을 진행하기 위해서이다.

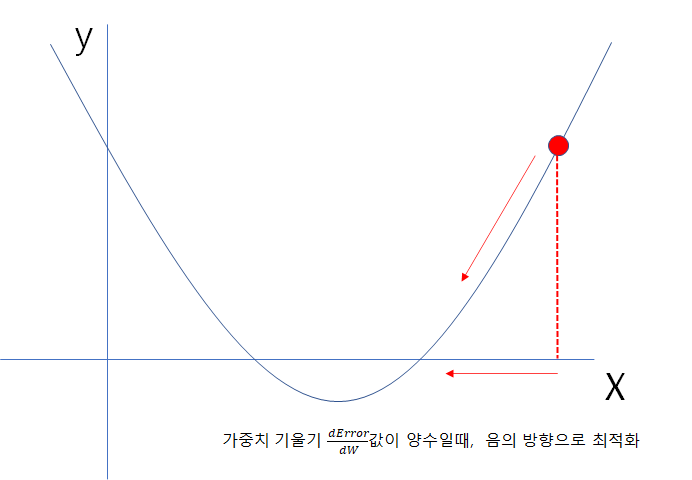
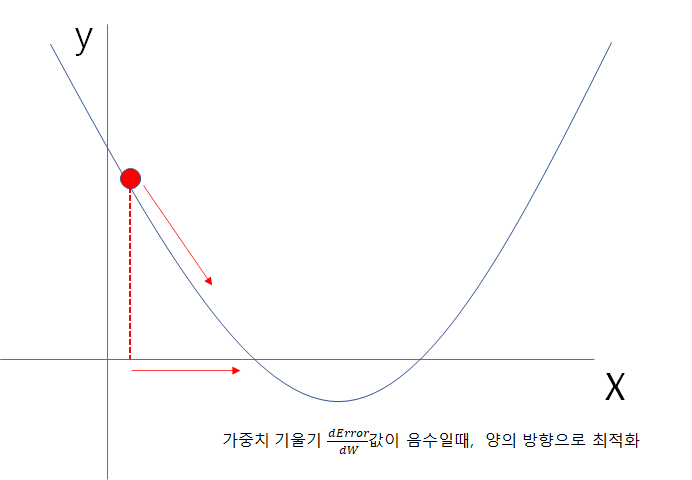
이미지와 같이 미분값이 결정되고 부호가 정해졌을때 항상 오차의 최소가 되는 최적화를 위해 경사하강법을 진행하는데, 기울기의 부호와 반대방향으로 이동해야 하기 때문에 음의부호(-)를 가중치 기울기에 붙여 진행하게 된다.

덧셈 노드의 역전파

덧셈 노드에 대한 역전파의 결론은 다음 노드로부터 되돌아온 연쇄법칙 미분값이 그대로 전달 된다는 것이다. 아래는 이를 증명하는 내용이다.

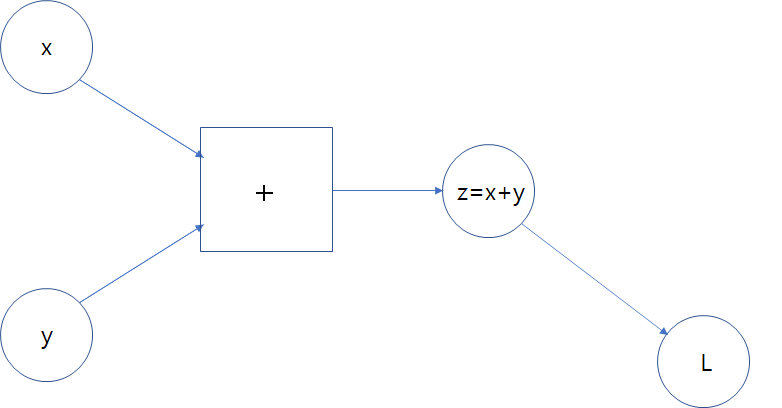
먼저 위 순전파 이미지를 확인해보면 $z = x+y$의 구조이며, $z$도 그 다음 노드와 어떠한 연산을 통해서 L이 생성되는 구조를 예시로 들고 있음을 알 수 있다.

역전파는 맨 마지막의 결과L로부터 역으로 돌아오며 편미분 연쇄법칙을 진행하는 것이므로 이러한 덧셈 연산을 가진 노드의 역전파는 아래와 같이 볼 수 있다.

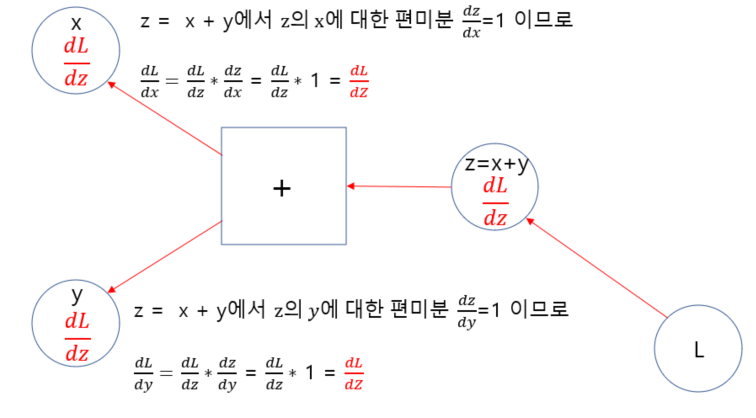
L의 x에 대한 편미분 값을 역전파로 구하는 식 $\frac{\delta L}{\delta x}=\frac{\delta L}{\delta z}*\frac{\delta z}{\delta x}$
L의 y에 대한 편미분 값을 역전파로 구하는 식 $\frac{\delta L}{\delta y}=\frac{\delta L}{\delta z}*\frac{\delta z}{\delta y}$

1. 우선 z의 x에 대한 편미분값을 구해본다.

   • z= x+y에서 z를 x로 편미분하면, y는 상수취급되어 사라지게 된다.
   • 남은 x가 미분되어 1이 된다.

2. 연쇄법칙에 따라 이전 L의 z에 대한 미분값을 곱해준다.

   • $\frac {\delta L}{\delta z}*1 = \frac {\delta L}{\delta z}$

3. 이는 y에 대한 편미분값도 동일하기 때문에, 결과적으로 덧셈노드의 역전파는 각 덧셈연산 이전에 있던 노드들로 이전 미분값$(\frac {\delta L}{\delta z})$가 그대로 전달 되는 것을 알 수 있다.

곱셈 노드의 역전파

곱셈 노드의 역전파는 덧셈과는 약간 다르지만 이 역시도 규칙이 생기는데, 이는 역전파 진행 시 다음 노드의 미분값에 구하고자 하는 대상이 아닌 구하고자 하는 대상과 '곱해진 값'을 곱해주는 것이다. 말로 풀어쓰니 설명이 힘든데, 그림과 수식으로 보자.

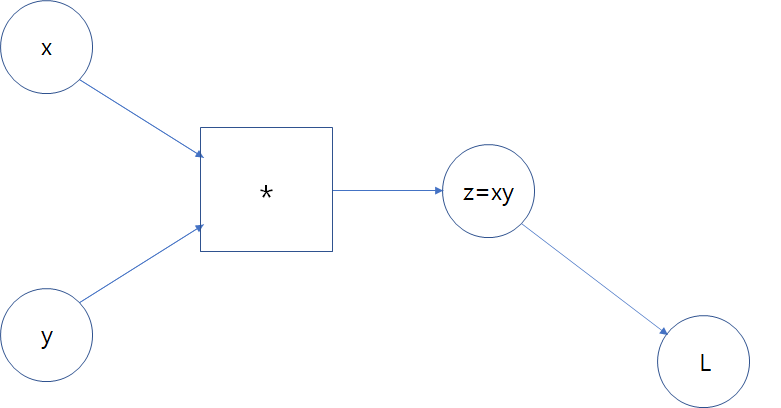
위 이미지는 x노드와 y노드를 곱셈연산$(*)$하여 $z=xy$라는 값의 z 노드가 된 것을 보여준다.
이를 역전파를 진행하면 다음 이미지와 같다.

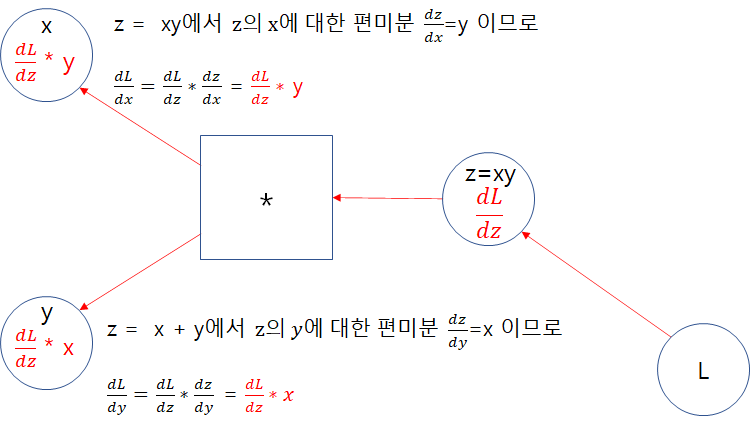
1. 우선 z의 x에 대한 편미분값을 구해본다.

   • $z= xy$에서 $z$를 $x$로 편미분하면, $y$는 상수취급되어 $x$에 곱해지게 된다.
     예를 들어, $y$가 2였다고 가정하면 $2x$가 된다.
   • 그 후 남은 $x$가 미분되면 1이 된다.
   • 결론적으로 $z=xy$의 $x$에 대한 편미분 값 $(\frac {\delta z}{\delta x})$은 2 * 1이 되고 수식상으로는 $y$가 된다.

2. 연쇄법칙에 따라 이전 L의 z에 대한 미분값을 곱해준다.

   • $\frac {\delta L}{\delta z}*y$

3. 이는 y에 대한 편미분값에서도 동일하게 적용되므로, 곱셈노드의 역전파는 각 곱셈연산을 했던 노드를 제외한 '곱셈의 대상노드'들을 곱해주게 되는 방식이다.