백준 15486 퇴사2 자바

문제는 다음과 같다.
https://www.acmicpc.net/problem/15486

---

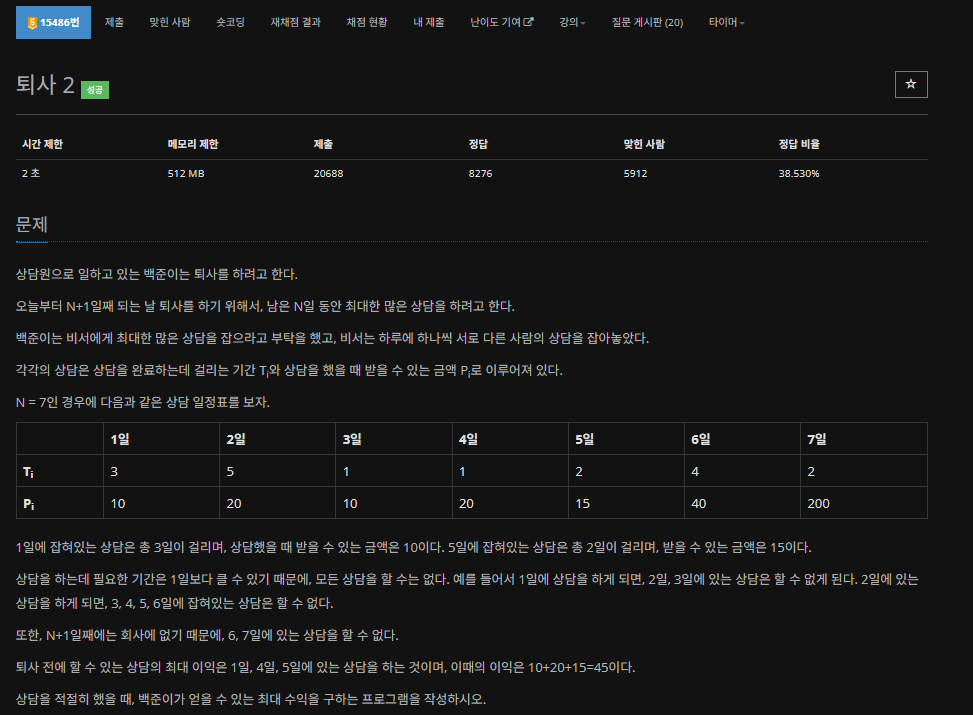
간략하게 말하면, 퇴사날과 스케줄이 정해졌을 때 최댓값의 이익을 뽑아내는 것이다.

예시 테스트케이스는 위 사진의 표가 있을때,
1, 4, 5,일에 있는 상담을 하고
45의 이익을 내는 것이다.

1일 상담 - 걸리는 날 3일, 얻는 돈 5, 마치는 날 4일
3일 상담 - 걸리는 날 1일, 얻는 돈 20, 마치는 날 4일
4일 상담 - 걸리는 날 1일, 얻는 돈 20, 마치는 날 5일
5일 이후의 날들은 상담 마치는 날이 퇴사날을 넘어서므로, 상담할 수 없다.

위 문제를 어떻게 풀어야 할까?
주어진날(n)의 범위가 150만 이하이고 시간제한은 2초이다.

n^2만 되더라도 150만의 제곱은
10의 12승이 되므로, 2억을 아득히 초과한다.
즉 n^2의 시간복잡도도 허용하지 않는 것이다.

그렇다면,
다이나믹 프로그래밍으로 O(n)의 시간복잡도로 풀어야 한다.

i일의 최대 이익을 D[i] 라고 하자.
그럼 D[i]는 어떻게 구해야 할까?

1. i일 이전의 값들을 보며, i일에 마치는 일정들을 계산하며 최댓값을 구한다.

2. i일부터 시작하는 일정의 마치는 날짜를 보며, 계산해준다.
   (마치는 날짜가 퇴사날보다 뒤라면, 그 일정은 잡을 수 없기 때문)

정답은 2번이다.

1번은 i일에 마치는 일정을 계산하기 위해서는
2중 for문의 n^2의 시간복잡도가 필요하고,

2번은 1중 for문의 n의 시간복잡도가 필요하다.

1번 2번 두개의 풀이를 보며 이해하도록 하자.
이해를 돕기 위해 주석을 곳곳에 달아놓았다.

---

1번 풀이 (n^2시간복잡도라 오답)

import java.util.*;
import java.io.*;

public class Main {

    public static void main(String args[]) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int n  = Integer.parseInt(br.readLine());
        
        int[][] arr = new int[n+1][2];
        for(int i = 1 ; i <= n ; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            arr[i][0] = Integer.parseInt(st.nextToken()); //i일 부터 걸리는 날짜 저장
            arr[i][1] = Integer.parseInt(st.nextToken()); //받을 수 있는 보수 저장
        }

        int[] D = new int[n+2]; //n+1일에 퇴사하니까, n+1일까지 일할 수 있다.
        //D[i] = i일 까지 일했을때 벌 수 있는 돈의 최댓값

        for(int i = 2 ; i <= n+1 ; i++) {
            for(int j = 1 ; j <= i-1 ; j++) {
                if(j + arr[j][0] <= i && D[i] < D[j] + arr[j][1]) D[i] = D[j] + arr[j][1];
                //j + arr[j][0] <= i , 시작 날짜 j와 걸리는 날짜 arr[j][0]을 더했을때, 현재 날짜 i보다 작거나 같아야 하고,

                //시작날짜까지 번 금액의 최댓값 D[j]와 벌어들이는 돈 arr[j][1]을 더한 값이
                //현재 날짜까지 벌 수있는 돈의 최댓값 D[i]보다 크다면 갱신해준다.
            }
        }

        int answer = 0;
        for(int i = 2 ; i <= n+1 ; i++) {
            answer = Math.max(answer, D[i]);
        }

        System.out.println(answer);

    }

}

---

2번 풀이 (n 시간복잡도, 이게 정답)

import java.util.*;
import java.io.*;

public class Main {
    public static void main(String args[]) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        
        //D[i] = i일에 벌 수 있는 돈의 최댓값
        //i일에 앞으로갈지 뒤로 갈지 생각해야 함.
        //이말이 무슨말이냐면, i일에 일을 마치는지, i일에 일을 시작하는지를 생각해보자.
        //전자로 한다면, i일 이전의 친구들을 모두 둘면서, 시작날 + 걸리는날 = i일 인 친구들을 다 찾아야함
        //후자라면, i일 + 걸리는날 의 값에 따라 하나씩만 해주면 됨.

        //즉, 전자는 2중 for문으로 N^2가 되고, 후자는 1중 for문으로 N이 되어 풀릴 수 있게 되는것임.

        int n = Integer.parseInt(br.readLine()); //퇴사 날짜
        int[][] arr = new int[n+1][2];
        //arr[i][0] -> i일에 잡힌 상담이 걸리는 날짜
        //arr[i][1] -> i일에 잡힌 상담으로 벌 수 있는 돈
        for(int i = 1 ; i <= n ; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            arr[i][0] = Integer.parseInt(st.nextToken());
            arr[i][1] = Integer.parseInt(st.nextToken());
        }

        int[] D = new int[n+2];
        //D[i] = i일에 벌 수 있는 돈의 최댓값, n+1일에 퇴사이므로 n+1까지.

        //내가 풀 생각은, i일 당일 현재로써 최대로 벌 수 있는 돈 D[i]에서
        //해당 날의 상담에 따라 D[i + i일의 상담에 걸리는 날] 이런식으로 찾아갈 예정.
        //이를 위해서는, D[i]는 항상 최댓값이어야 하기 때문에, 로직이 필요함.

        int max = 0; //여기가 D[i]를 최댓값으로 유지해줄 친구
        for(int i = 1 ; i <= n ; i++) {
            max = Math.max(D[i], max);
            D[i] = max;
            if(arr[i][0] + i > n+1) continue; //지금 날짜와 걸리는 날짜의 합이 퇴사날을 넘어선다면, 제끼기

            if(arr[i][1] + D[i] > D[i + arr[i][0]]) D[i + arr[i][0]] = arr[i][1] + D[i];
            //잘 읽기
            //지금 날짜까지 벌 수 있는 최대의 돈과 일을 마치는날 벌어들이는 돈의 합이
            //지금까지 기록한 일을 마치는날 버는 돈의 최댓값보다 크다면 갱신해주기
            //예를 들어, i = 3, D[3] = 5, arr[3][0] = 3, arr[3][1] = 10, D[6] = 5 일때,
            //3일까지 최대로 버는 돈은 5이고, 3일에 시작하는 일이 3일이 걸려 6일에 마치고, 해당 일로 10원을 벌 수 있을때,
            //현재 6일까지벌 수 있는 돈은 5이므로, (arr[3][1])10 + (D[3])5 > (D[3 + arr[3][0]])6 이므로 갱신된다.
        }

        //이제 기록된 값들 중 최댓값이 벌 수 있는 돈의 최댓값이다.
        int answer = 0;
        for(int i = 1 ; i <= n+1 ; i++) {
            answer = Math.max(answer, D[i]);
        }

        System.out.println(answer);
        
    }

}

1번 풀이는
지금 문제인 퇴사 2가 아니라
14501, 퇴사 문제는 풀릴 수 있다.

하지만, 어떻게든 푸는게 중요한게 아니라, 알고리즘과 시간복잡도를 항상 고려하며 풀어야 한다.