백준 1915 가장 큰 정사각형 자바

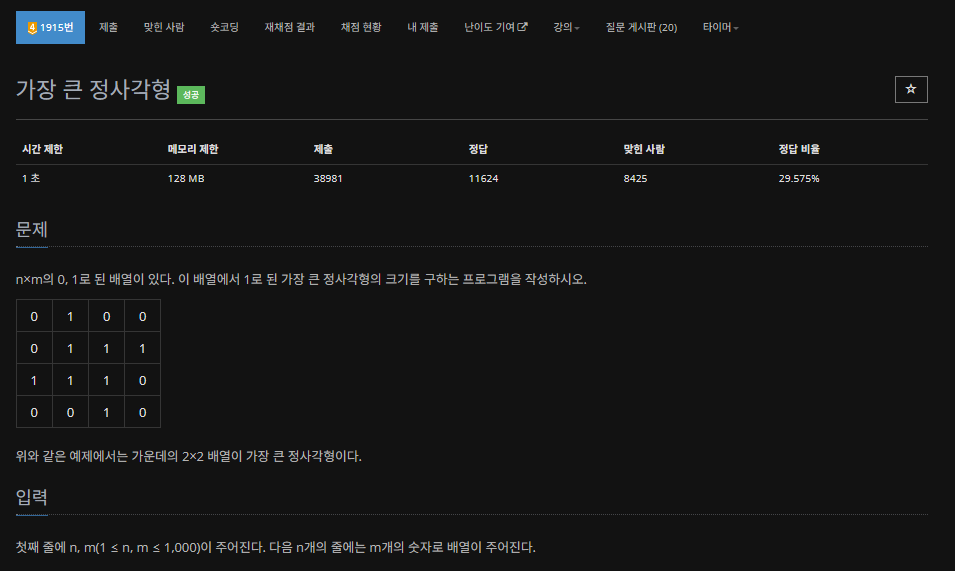
문제는 다음과 같다.
https://www.acmicpc.net/problem/1915

---

풀이는 다음과 같다.

import java.util.*;
import java.io.*;

public class Main {
    public static void main(String args[]) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine());

        int R = Integer.parseInt(st.nextToken());
        int C = Integer.parseInt(st.nextToken());

        int[][] D = new int[R][C];
        int answer = 0;

        for(int r = 0 ; r < R ; r++) {
            String s = br.readLine();
            for(int c = 0 ; c < C ; c++) {
                D[r][c] = Integer.parseInt(s.substring(c, c+1));
                if(D[r][c] == 1) answer = 1;
                //바로 위의 로직은, 직사각형이 1 일때 예외를 위해 해준다.
            }
        }


        for(int r = 1 ; r < R ; r++) {
            for(int c = 1 ; c < C ; c++) {
                if(D[r][c] == 0) continue; //현재 점이 0이라면, 해당 점으로는 정사각형을 만들 수 없다.
                D[r][c] = Math.min(D[r-1][c-1], Math.min(D[r-1][c], D[r][c-1])) + 1;
                answer = Math.max(answer, D[r][c]);
            }
        }

        bw.write(String.valueOf(answer * answer));
        bw.flush();
        bw.close();


    }

}

---

R행 C열의 직사각형의 안에서,
1로 이루어진 가장 큰 정사각형을 찾는 문제이다.
그런데, 행과 열의 최댓값은 1000이고,
하나하나 모든 정사각형을 찾아낼 수는 없다.

DP, 다이나믹 프로그래밍 문제이다.

D[i][j] 를 i, j를 왼쪽 아래 꼭짓점으로 하는 정사각형의 최대 크기
라고 정의한채로 문제를 풀 수 있다.

그렇다면, 아래와 같은

D[r][c] = Math.min(D[r-1][c-1], Math.min(D[r-1][c], D[r][c-1])) + 1;

점화식을 어떻게 도출해야할까?

아래 그림을 보자.

r-1,c-1, 에는 2X2 정사각형이,
r, c-1에는 1X1 정사각형이,
r-1, c에는 3X3 정사각형이 있다.

이제 r c에 들어갈 정사각형을 생각해보자.

노란색으로 칠해진 부분이 r행 c열을 마지막으로 하는 정사각형중, 최댓값이 된다.

위 그림을 보며 설명한다면 아래와 같다.
즉 r행 c열을 마지막으로 하는 가장 큰 정사각형은
r, c-1 1X1 정사각형 크기 + 1이 되는것이다.
셋 중 가장 작은 정사각형을 택할 시,
나머지 정사각형들 (r-1, c-1과 r-1, c 정사각형) 은 양변의 길이가 더 길기 때문에
가장 작은 정사각형을 + 1으로 확장할 수 있는 것이다.

지금까지의 설명을 점화식으로 도출하면, 셋 중 가장 작은 값 + 1 이므로

D[r][c] = Math.min(D[r-1][c-1], Math.min(D[r-1][c], D[r][c-1])) + 1;

이렇게 된다.