Backpropagation
이전 시간까지 가중치(W)는 손실함수(Cost function)를 감소시키는 방향으로 개선되어야한다는 것을 배웠다. 결국 손실함수는 실제값과 예측값의 차이에대한 함수이고 경사하강법을 통해 이 함수의 미분 즉 입력에대한 손실함수의 변화를 계산해서 손실이 작아지는 쪽으로 가중치 값들을 변화시키는 것이다.
그렇다면 깊은 신경망에서 어떻게 손실함수의 각 layer의 가중치들과 손실함수 에러와의 관계를 알 수 있을까?
이를위한 방법이 오류역전파(backpropagation)이다.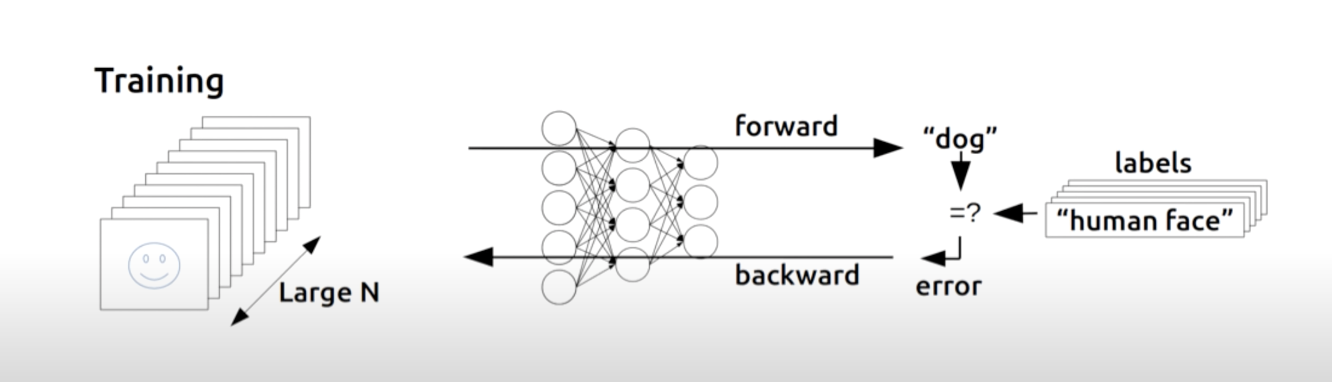
Backpropagation의 원리
우선 아래와 같은 간단한 신경망의 구조를 보자. 우리의 목적은 예측함수 f로 부터 유도되는 손실함수를 낮추는 것이며 이를위해 매개변수(w,b)들을 갱신해주어야한다. 이때 매개변수를 어떻게 갱신해주어야하는지는 입력에 대한 출력의 변화량인 미분으로부터 구해줄 수있다.미분이 입력이 변했을 때 출력이 얼만큼 변하는지의 관계를 알 수 있는 방법이기 때문이다.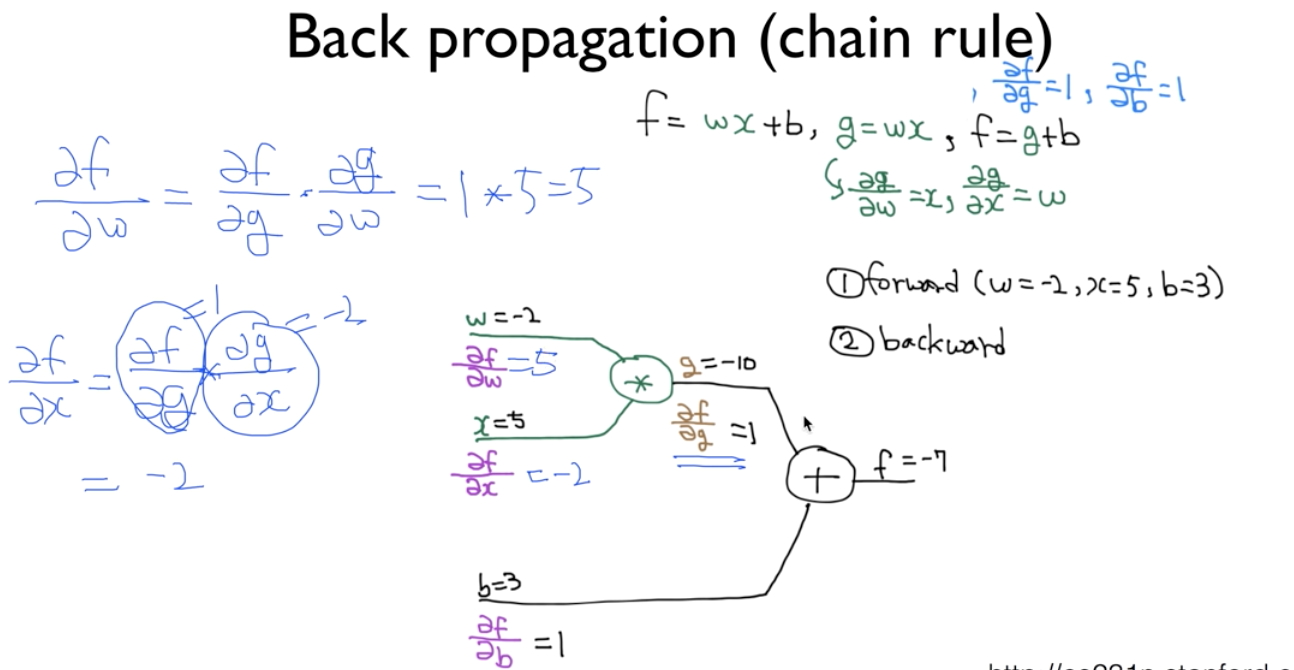
깊은 신경망에서도 마찬가지이다. 다만 layer가 여러개가 되었을 때 입력대한 출력의 변화를 알기가 어렵다는 문제가있다. 하지만 우리가 고등학교 때 배운 chain rule을 적용해 이 문제를 해결할 수 있다. 처음 입력에대한 다음 출력의 변화량, 그 출력이 다음 layer의 입력이되어 또 그 다음 출력에대한 변화량 이런식으로 최종 출력까지의 변화량을 곱해 에러에대한 각 layer들의 매개변수와의 관계(변화량)를 알 수있다. 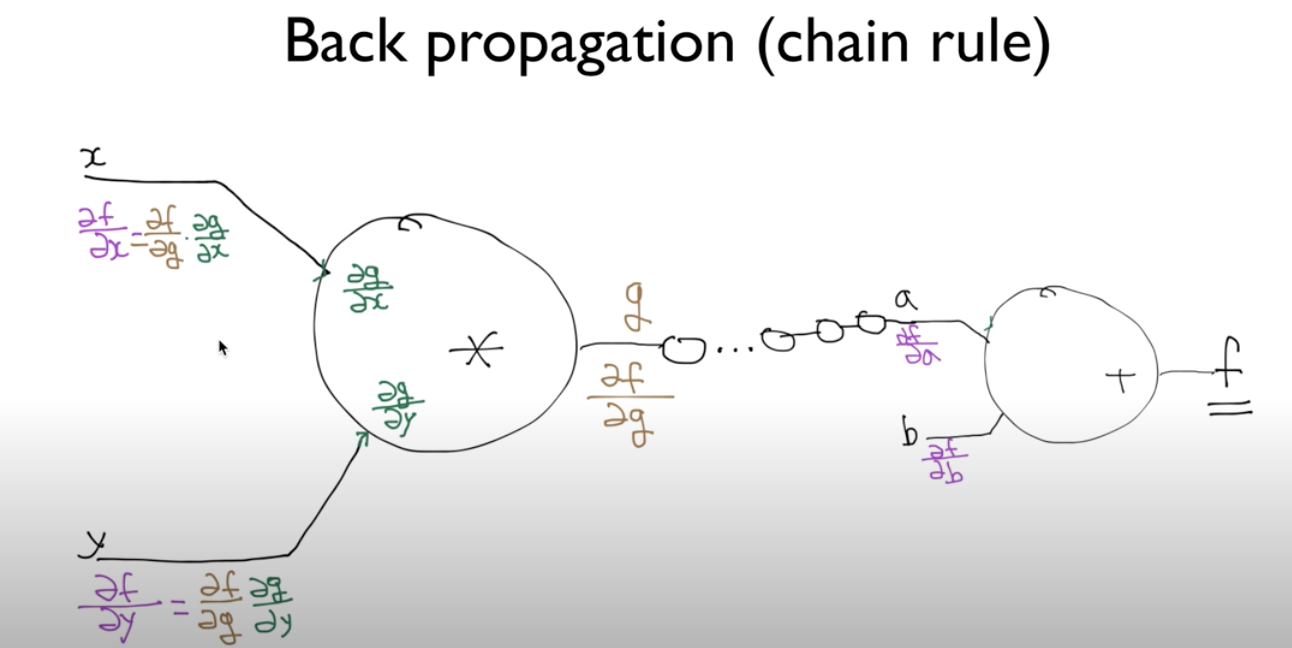
Gradient Vanishing
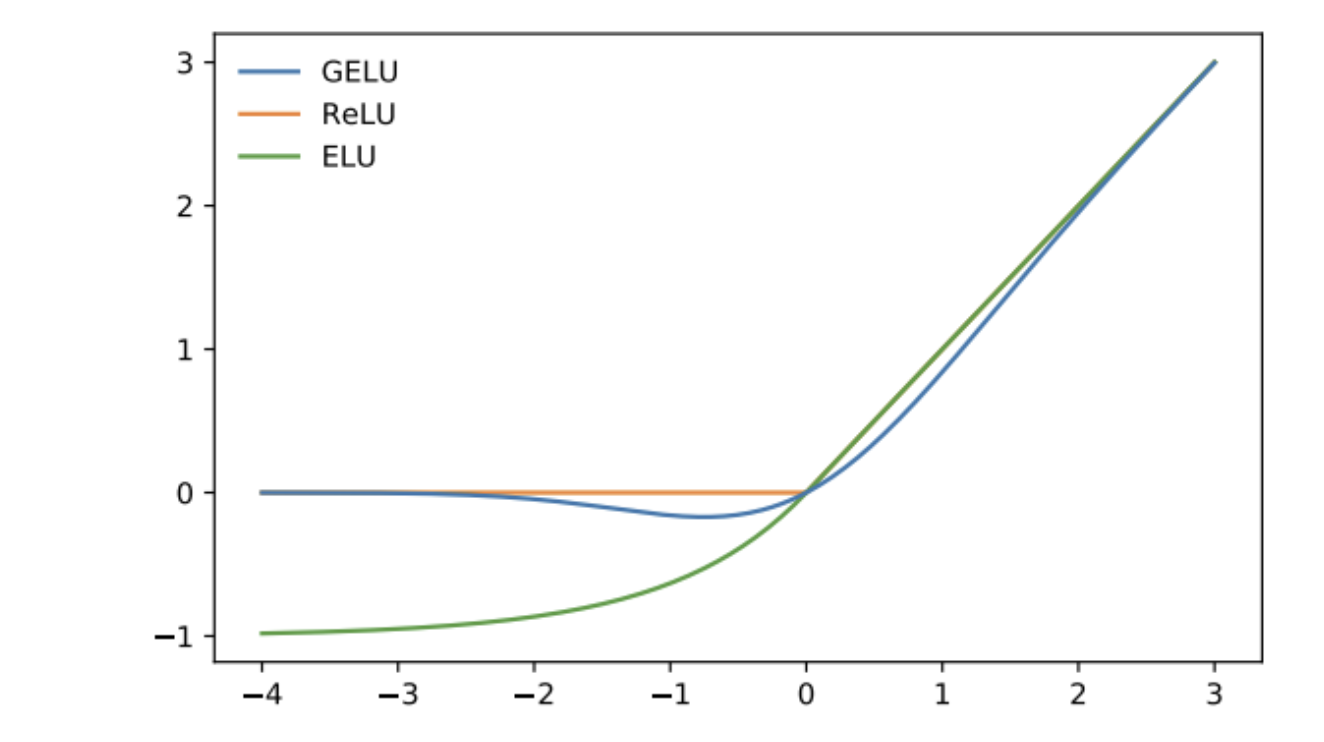
깊은 신경망에서 활성함수로 sigmoid를 사용하면 한가지 문제가 발생한다. 활성함수가 각 layer에서 작동한다고 했을 때 비선형의 sigmoid 함수 특성상 양쪽 끝부분에서 기울기가 0에 가까운 지점이 존재하기 때문이다. 결국에는 chain rule이란 것이 각 layer의 변화량을 전부 곱해서 입력에대한 출력의 관계를 알기위함인데 변화량이 0에 가깝게된다면 관계를 알 수가 없다.
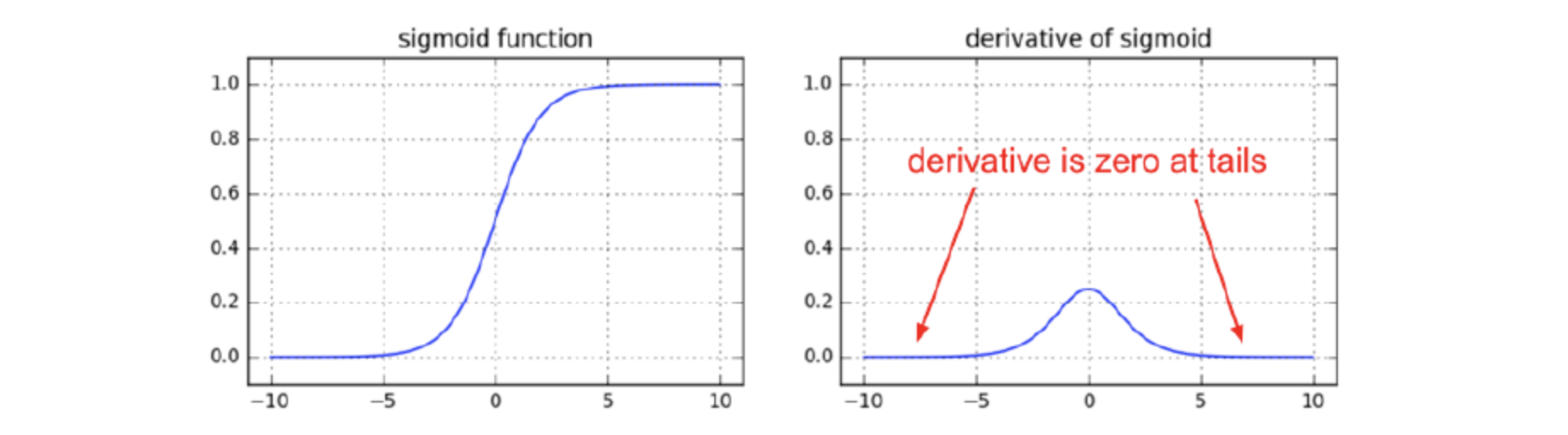

따라서 layer 개수가 많은 신경망의 경우 아래와 같이 간단한 형태의 ReLU 함수를 활성함수로 사용한다. 하지만 ReLU함수도 0이하의 입력에서는 기울기가 사라지므로 최근에는 0이하에서도 약간의 기울기를 가지고있는 GELU함수를 많이 사용한다고한다.