[Day1] 오리엔테이션 & 자료구조와 알고리즘

이석영·2020년 12월 1일

Programmers

목록 보기

1/47

프로그래머스 인공지능 데브코스 첫 날
꼭 참여하고 싶었고 어렵게 함께하게 된 만큼 열심히 할 생각이었는데, 첫 날부터 학습량이 만만치가 않다.
하지만 내가 개발자가 되기위해 공부한 기간이 얼마안되기 때문에 어려운 것이 당연하고 같이 참여하는 동기들보다 많이 부족하다고 스스로 느끼기 때문에 남들보다 두세배 더 열심히 해볼 생각이다.
이 공간에는 앞으로 그날 그날 배운 것들 중 내가 알고는 있었지만 정확하지 않았거나 배우면서 어렵다고 느끼는 것들 그리고 새롭게 알게된 것들을을 기록하면서 복습하고 정리하겠다.

자료구조란?

자료구조(Data Structure)란 컴퓨터 과학에서 효율적인 접근 및 수정을 가능케하는 자료의 조직, 관리, 저장을 의미한다. 자세히는 데이터 값의 모임 또는 관계, 그리고 데이터에 적용가능한 함수나 명령으로 적절한 자료구조의 선택은 효율적인 알고리즘을 사용 할 수 있게한다.
< 위키피디아 참고>

알고리즘이란?

수학과 컴퓨터 과학, 언어학 또는 관련 분야에서 어떠한 문제를 해결하기 위해 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것, 계산을 실행하기 위한 단계적 절차를 의미한다.
< 위키피디아 참고>

자료구조와 알고리즘의 차이가 딱 나누어 떨어지지않아 둘의 의미를 좀 혼동했다. 찾아보니 다른 사람들도 많이 둘의 구분에대해 어려워하는 것 같은데, 내가 이해한대로라면 자료구조는 데이터가 저장되는 형태 또는 표현을 의미하고 알고리즘은 그러한 자료구조를 어떤 순서, 규칙으로 어떻게 처리할 것인가를 말한다.

결국 자료구조와 알고리즘은 모두 문제를 효과적으로 해결하기위함이 목적이고 문제유형에 따라 적절한 자료구조와 알고리즘은 다르다. 여기서 효과적이란 시간(실행속도)과 공간(메모리) 자원을 최소한으로 사용하는 것을 의미한다.

정렬

sorted(list) & list.sort()

L2 = sorted(L, reverse = True)
// 리스트 L을 내림차순으로 정렬, 리스트 자체가 변경되지 않으므로 별도 변수에 할당필요
L.sort(reverse = True)
// 마찬가지로 리스트 L을 내림차순으로 정렬하는데 위와 다르게 리스트 L자체가 변경된다

문자열 길이 순서로 정렬

 L = ['abcd', 'xyz', 'spam']
 sorted(L, lambda x: len(x))
 
 결과 : ['xyz','abcd', 'spam']

Dictionary에서 key를 지정해 정렬하는 예

L=[{'name' : 'John', 'score': 82}, {'name' : 'Paul', 'score': 92}]

L.sort(key = lambda x: x['name'], reverse =True) 
//  name의 알파벳 내림차순 순서로 정렬됨
결과 [{'name': 'Paul', 'score': 92}, {'name': 'John', 'score': 82}]
L.sort(key = lambda x: x['score'], reverse=True)
// score 점수가 내림차순 순으로 정렬됨
결과 [{'name': 'Paul', 'score': 92}, {'name': 'John', 'score': 82}]

위에서 lamba 함수를 사용했는데 이는 함수를 간편하게 정의하는 방법이다. 단, def 함수와 같이 정의해서 계속사용하는 것이 아니라 일시적 사용을 위한 함수다.
간단한 예시를 들면

result = lambda a,b : a+b
print(result(4,5))
// 9

map() 함수와도 함께 사용가능하다.
마찬가지로 예시를 들면

L1 = [1,2,3]
L2 = [4,5,6]
result = list(map(lambda a,b : a+b, L1,L2)) ## 리스트 L1,L2의 원소를 받아 lambda함수 적용
print(result)
// [5,6,9]

선형탐색

순차적으로 모든 요소를 탐색
리스트 길이에 비례하는 시간요소 : 선형의 복잡도 O(n)를 가진다
최악의 경우 모든 원소를 다 비교할 수 있음

이진탐색

한번 비교가 일어날 때마다 리스트를 반씩 줄여가면서 탐색
O(logn) 복잡도를 가진다

def solution(L, x):
    answer = 0
    lower = 0 ## 탐색시작 인덱스
    upper = len(L) - 1 ## 탐색종료 인덱스
    
    if x not in L:
        return -1
    
    while lower <= upper:
        
        middle = (lower + upper) // 2
        
        ## x가 중앙값일 경우 그 값의 인덱스 리턴
        if L[middle] == x:
            return L.index(x)
            
        ## x가 L의 중앙값보다 큰 경우 : 탐색시작 인덱스를 middle값으로
        elif L[middle] < x:
            lower = middle
        ## x가 L의 중앙값보다 작은 경우 : 탐색종료 인덱스를 middle값으로 
        else:
            upper = middle

재귀 알고리즘/함수

하나의 함수에서 자기 자신을 다시 호출하여 작업을 수행하는 것
종결조건이 매우 중요
복잡도 : O(n), 효율성이 반복적(iterative)알고리즘 보다 떨어질 수 있음

재귀 알고리즘 예시 (피보나치 수열)

def solution(x):
    answer = 0
    if x <= 1:
        answer = x
    else:
        answer = solution(x-1) + solution(x-2)

    return answer

여기서부터는 내가 처음 접하는 내용들이 대부분이라 이해하기가 점점 힘들기 시작했다.
매일매일의 학습량이 방대해 따라가기도 벅차지만 틈틈히 아래 내용들은 따로 찾아보고 공부해서
계속해서 내용을 보완하겠다.

연결리스트(Linked Lists)

각 원소를 줄줄이 엮어 관리하는 방법
선형배열과같이 데이터 원소를 순서대로 늘어놓는다는 점은 같이만 방식에있어 차이가 있고 특정 원소를 삽입, 삭제하는 것이 더 빠르다. 따라서 원소의 삽입/삭제가 빈번히 일어나는 시스템에 주로쓰인다.
예를들면, 휴대폰 백그라운드 앱을 열면 순서대로 되어있고 그중 하나를 종료하는 경우
선형배열대비 단점으로는 메모리 공간소요가 크다. 또한 예를들어 k번째 원소를 찾을 때는 더 시간이 오래 걸린다. 선형배열에서는 인덱스로 찾으면되지만 연결리스트는 앞에서부터 하나하나 링크를 따라가면서 찾아야 한다.
node의 연결?
- 앞에있는 node가 뒤에있는 node를 가르킨다.
- node는 값인 data와 다음node를 가르키는 link를 담고있다.

연결리스트의 연산에는 다음과 같이 6가지가 있다.

임의의 K 번째 원소 참조

리스트 순회(traverse)

전체 리스트 길이얻어내기

리스트의 원소추가

리스트의 원소삭제

두 리스트 합치기

추상적 자료구조란 무엇?

내부 구현은 숨겨두고 밖에서 보이는 것 두가지(데이터, 연산)를 제공
. 데이터 : 정수, 문자열, 레코드....
. 삽입, 삭제, 순회, 정렬, 탐색...

생성자(Constructor)

생성자 : 객체를 생성할 때 호출되는 함수로 객체 생성 시 초기화 작업을위해 존재한다.
연결리스트의 node를 생성자로 초기화하는 다음과 같다.

## Node라는 명의 클래스 정의
class Node:
	## item이라는 인자를 받는 초기화 함수
	def __init__(self, item): 
    		## 객체생성 : 변수data를 item으로 초기화, 변수 next를 None으로 초기화
    		self.data = item 
    		self.next = None

## LinkedList 클래스 정의
class LinkedList:
	def __init__(self):
    		## 연결리스트 개수 초기화
    		self.nodeCount = 0
        	## 처음, 마지막 node 초기화
        	self.head = None
        	self.tail = None

양방향 연결 리스트(Doubly Linded Lists)

양방향으로 링크가 연결된 리스트로 앞의 node로도 뒤의 node로도 이동이 가능하다.
리스트의 처음과 끝에 dummy node를 둔다. 그전까지는 head에만 dummy node가 있었다.

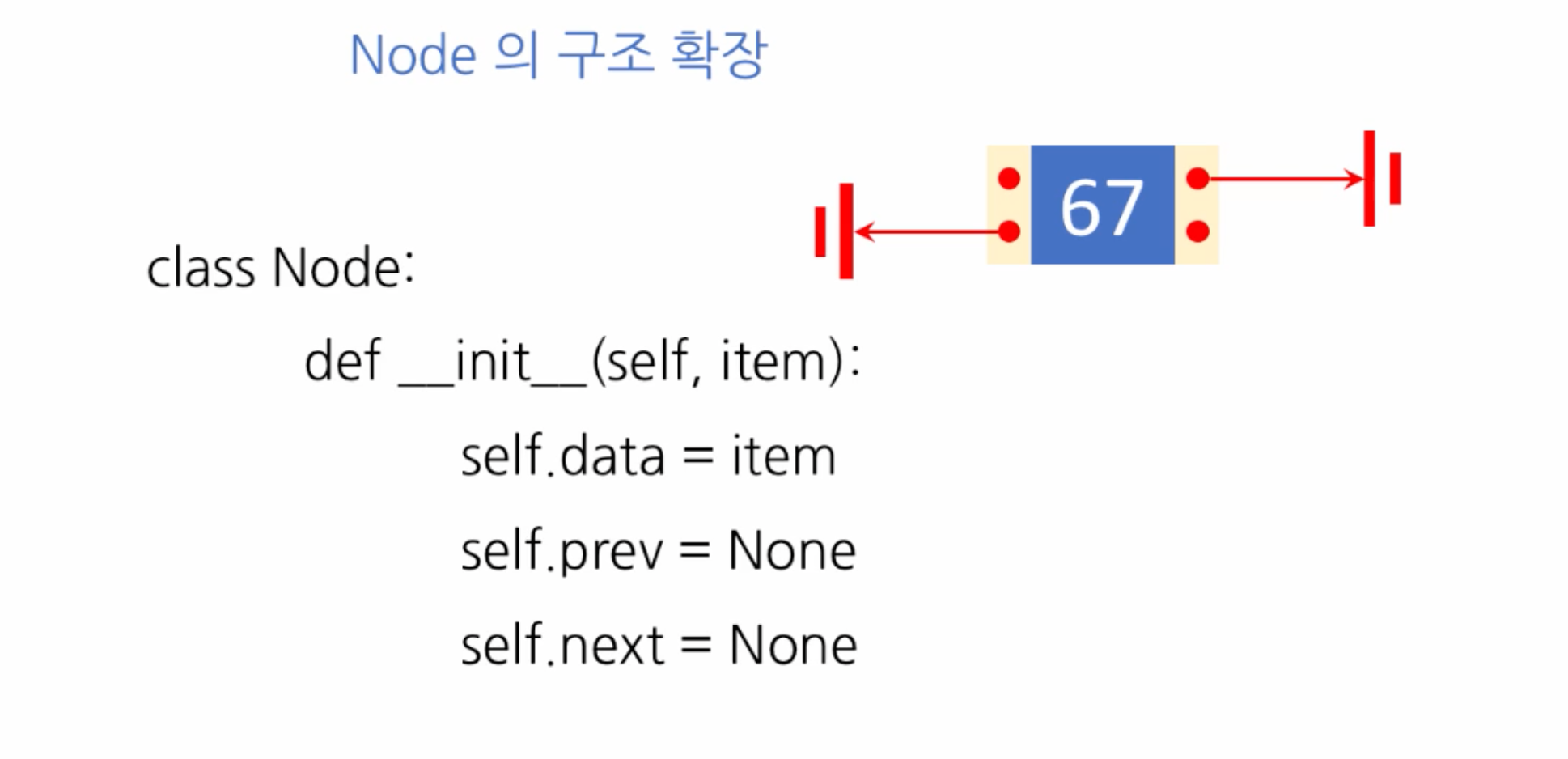
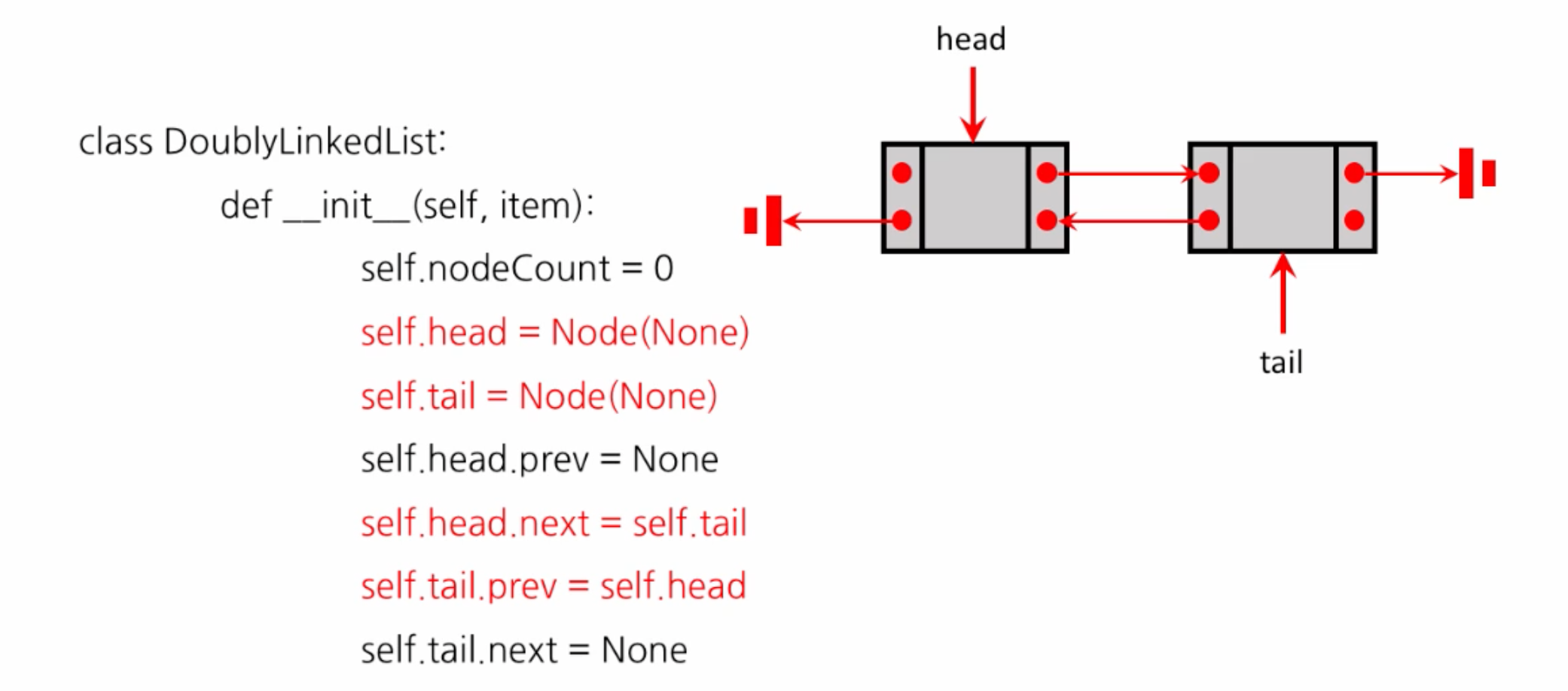
## 노드 생성,초기화
class Node:
    def __init__(self, item):
        self.data = item
        self.prev = None
        self.next = None
## 양방향 연결리스트 생성, head와 tail에 None으로 초기화해준 것을 볼 수 있다.
class DoublyLinkedList:
    def __init__(self):
        self.nodeCount = 0 ## dummy node는 빼고센다
        self.head = Node(None)
        self.tail = Node(None)
        self.head.prev = None
        self.head.next = self.tail
        self.tail.prev = self.head
        self.tail.next = None

    ## 역순회
    def reverse(self):
        result = []
        curr = self.tail 
        while curr.prev.prev:
            curr = curr.prev
            result.append(curr.data)
            
        return result
    
    ## 원소 탐색, 인자를 위치 pos로 받았다.
    def getAt(self, pos):
        if pos < 0 or pos > self.nodeCount:
            return None
		## 탐색속도를위해 중간위치에서 왼쪽인지 오른쪽인지 확인
        ## 중간보다 뒤에있으면 tail에서부터 탐색 
        if pos > self.nodeCount // 2:
            i = 0
            curr = self.tail
            while i < self.nodeCount - pos + 1:
                curr = curr.prev
                i += 1
        ## 중간 앞에있으면 head에서부터 탐색        
        else:
            i = 0
            curr = self.head
            while i < pos:
                curr = curr.next
                i += 1
        return curr

    ## 원소 삽입, 이전 node(prev)와 새로운 node를 인자로 받는다.
    def insertAfter(self, prev, newNode):
        next = prev.next
        newNode.prev = prev
        newNode.next = next
        prev.next = newNode
        next.prev = newNode
        self.nodeCount += 1
        return True

    ## 또다른 방법, 위치 pos를 인자로 받는다.
    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False

        prev = self.getAt(pos - 1)
        return self.insertAfter(prev, newNode)

     ## 다음 node를 인자로 받아 삽입도 가능하다.
     def insertBefore(self, next, newNode):
            prev = next.prev
            newNode.prev = prev
            newNode.next = next
            prev.next = newNode
            next.prev = newNode
            self.nodeCount += 1
            return True

    ## 이전 node를 인자로 받아 원소삭제 
    def popAfter(self, prev):
            curr = prev.next
            prev.next = curr.next 
            curr.next.prev = prev
            curr.next = None
            curr.prev = None
            self.nodeCount -= 1 ## 요거 빼억지말자!

            return curr.data

    ## 다음 node를 인자로 받아 원소삭제
    def popBefore(self, next):
        curr = next.prev
        next.prev = curr.prev
        curr.prev.next = next
        curr.prev = None
        curr.next = None
        self.nodeCount -= 1
    
    ## 양방향 리스트의 결합, 결합할 양방향 리스트를 인자로받는다. 
    def concat(self, L):
        if self.nodeCount != 1 or L.nodeCount != 0:
            self.tail.prev.next = L.head.next
            L.head.next.prev = self.tail.prev
            self.tail = L.tail
            self.nodeCount += L.nodeCount ## dummy인 head, tail은 제외한 값이다.


def solution(x):
    return 0

스택(Stack)

자료를 보관하는 선형구조, 후입선출(LIFO) 자료구조
초기화 필요 : s = Stack()

제공하는 연산자

size() : 스택의 사이즈(원소의 개수)를 구함
isEmpty() : 스택이 비어있는지 판단, 비어있으면 self.size() == 0을 반환
push(x) : 원소 x를 스택에 추가
pop() : 가장 나중에 저장된 원소 제거 및 반환 self.data.pop(-1)
peek() : 가장 나중에 저장된 원소를 반환, 제거하지 않음

큐(Queue)

자료를 보관하는 선형구조, 선입선출(FIFO) 자료구조
큐 최기화 필요 : q = Queue()
큐의 추상적 자료구조 구현 : 배열이용, 양방향 연결 리스트 이용

제공하는 연산자

size() : 큐의 사이즈(원소의 개수)를 구함
isEmpty() : 큐가 비어있는지 판단, 비어있으면 self.size() == 0을 반환
enqueue(x) : 원소 x를 큐에 추가
dequeue() : 가장 나중에 저장된 원소 제거 및 반환 self.data.pop(0)
peek() : 가장 나중에 저장된 원소를 반환, 제거하지 않음

양방향 연결 리스트로 작성하는 큐

class Node:

    def __init__(self, item):
        self.data = item
        self.prev = None
        self.next = None


class DoublyLinkedList:

    def __init__(self):
        self.nodeCount = 0
        self.head = Node(None)
        self.tail = Node(None)
        self.head.prev = None
        self.head.next = self.tail
        self.tail.prev = self.head
        self.tail.next = None


    def __repr__(self):
        if self.nodeCount == 0:
            return 'LinkedList: empty'

        s = ''
        curr = self.head
        while curr.next.next:
            curr = curr.next
            s += repr(curr.data)
            if curr.next.next is not None:
                s += ' -> '
        return s


    def getLength(self):
        return self.nodeCount


    def traverse(self):
        result = []
        curr = self.head
        while curr.next.next:
            curr = curr.next
            result.append(curr.data)
        return result


    def reverse(self):
        result = []
        curr = self.tail
        while curr.prev.prev:
            curr = curr.prev
            result.append(curr.data)
        return result


    def getAt(self, pos):
        if pos < 0 or pos > self.nodeCount:
            return None

        if pos > self.nodeCount // 2:
            i = 0
            curr = self.tail
            while i < self.nodeCount - pos + 1:
                curr = curr.prev
                i += 1
        else:
            i = 0
            curr = self.head
            while i < pos:
                curr = curr.next
                i += 1

        return curr


    def insertAfter(self, prev, newNode):
        next = prev.next
        newNode.prev = prev
        newNode.next = next
        prev.next = newNode
        next.prev = newNode
        self.nodeCount += 1
        return True


    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False

        prev = self.getAt(pos - 1)
        return self.insertAfter(prev, newNode)


    def popAfter(self, prev):
        curr = prev.next
        next = curr.next
        prev.next = next
        next.prev = prev
        self.nodeCount -= 1
        return curr.data


    def popAt(self, pos):
        if pos < 1 or pos > self.nodeCount:
            raise IndexError('Index out of range')

        prev = self.getAt(pos - 1)
        return self.popAfter(prev)


    def concat(self, L):
        self.tail.prev.next = L.head.next
        L.head.next.prev = self.tail.prev
        self.tail = L.tail

        self.nodeCount += L.nodeCount


class LinkedListQueue:

    def __init__(self):
        self.data = DoublyLinkedList()

    def size(self):
        return 
self.data.getLength()


    def isEmpty(self):
        return 
self.data.getLength() == 0


    def enqueue(self, item):
        node = Node(item)

## 아래 둘다 가능
## insertAt은 인자로 pos와 newNode를 받음        
self.data.insertAt(self.data.getLength()+1, node)
## insertAfter는 인자로 prev와 newNode를 받음
self.data.insertAfter(self.data.tail.prev, node)


    def dequeue(self):
        return 
self.data.popAt(1)


    def peek(self):
        return 
self.data.getAt(1).data



def solution(x):
    return 0

이석영

원하는 대로 살자

다음 포스트