이번 파트의 목표는 어떤 연립일차방정식, 즉 linear system(선형시스템)이라도 정형적인 Ax = b와 같은 방법으로 표현해 해결하는 방법을 배우는 것이다.

선형시스템

선형 방정식(Linear equation)이란?

• 어떤 방정식이 직선과 같은형태로 올 곧게 표현된다면 선형방적이라고 할 수 있다.

선형방정식의 예

• 3x + y + z = 4
• x -2y -z = 1

비선형 방정식의 예

• sinx + y = 2
• 3x + y^3 = 2
• xy + z = 3 (xy 항이 2차항이므로 비선형 방정식이된다)

선형 시스템의 대수적 표현

• 아래와 같이 연립 방정식을 Ax = B 형태의 행렬로 표현하는 것
  

가우스 소거법(Gauss Elimination)

선형 시스템의 해

1. 해가 하나인 경우

• 3x = 6

2. 해가 존재하지 않는 경우

• 0x = 6
  이때 ax = b에서 a = 0이되는 꼴로 이처럼 a의 역수가 존재하지않으면 a가 특이(singular)하다고한다.

3. 해가 무수히 많은 경우

• 0x = 0

1과 3과 같이 해가 있으면 선형시스템이 consistent, 2와같이 해가 없으면 선형시스템이 inconsistent하다고한다.
위와 같은 상황들을 행렬로 표현하면 다음과 같다.
기하학적으로 생각해보면 해가 없는 경우는 두직선이 평행한 경우이고 해가 무수히 많은경우는 두직선이 겹치는 경우라고 볼수있다.

가우스 소거법

• 가우스 소거법은 임의의 m x n 선형시스템의 해를 구하는 가장 대표적 방법이다
• 다음 두 단계의 순서로 수행된다
• 두 단계가 진행되면 아주 간단한 형태인 upper triangular matrix가 되므로 계산이 편해진다.

1. 전방소거법(Forword elimination)

• 주어진 선형시스템을 아래로 갈수록 더 단순한 형태의 선형방정식을 가지도록 변형한다.
  

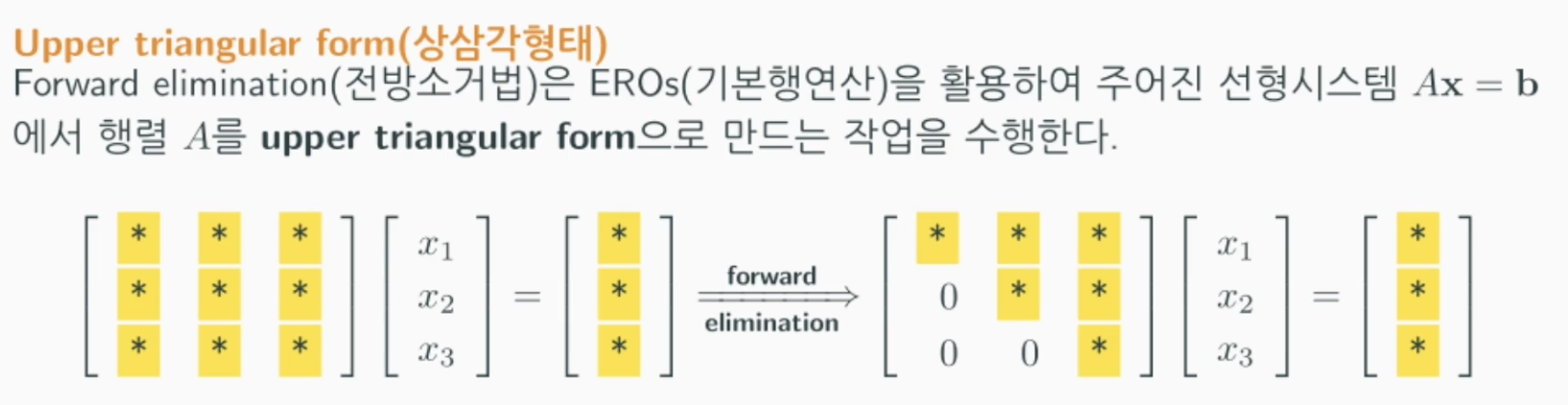
2. 후방대입법(Back substitution) : 아래에서부터 위로 미지수를 실제값으로 대체한다.

• 주어진 선형시스템의 rank를 알려준다. 실제 선형방정식의 수. 예를들어 해가 무수히 많은경우 방정식이 2개이지만 결국에는 같은 방정식이므로 rank는 2가 아닌 1이다.

• 선형시스템의 해가 있는지 없는지 알려준다.