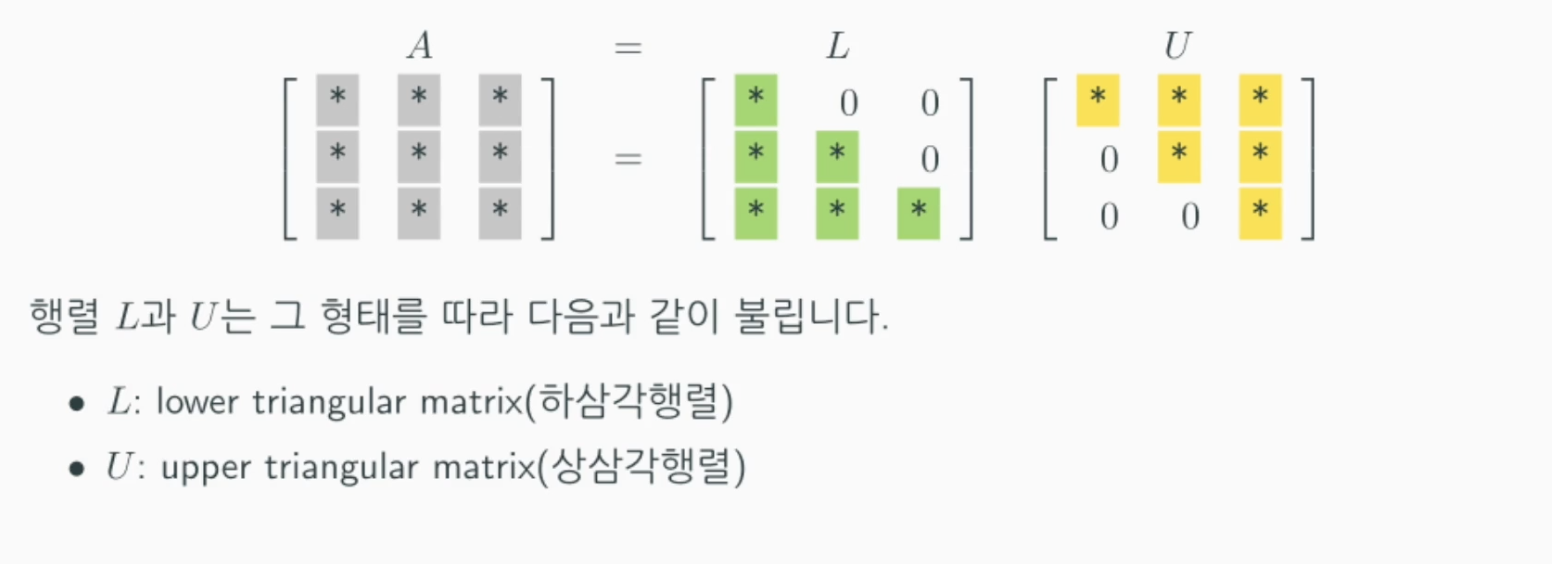
LU 분해
- Ax = b의 형태를 LUx = b와같이 변경할 때 A를 L과U의 곱인 LU로 분해하는 것을 말한다.
- LU분해의 목적은 x를 구할 때 A의 역행렬로써 구하는 것보다 수치적 안정성 높일 수 있기 때문이다.
- 또한 b가 자주 업데이트되는 경우 A를 PLU로(P는 옵션) 분해해 본다면 b가 업데이트될 때마다 x를 실시간으로 구할 수 있다.
LU분해 계산 흐름은 다음과 같다.
1. Ax = b
2. (LU)x = b
3. L(Ux) = b
4. Ly = b, 이러한 형태에서 L이 이전 강의에서 배운 가우스 소거법을 이용해 만든 하삼각행렬의 형태이므로 y를 매우 쉽게 구할수 있다.
5. Ux = y, U역시 가우스 소거법의 후방대치법을 이용한 결과의 형태이고 y 또한 위에서 알았으므로 x를 쉽게 구할 수 있다.

행렬연산과 선형조합
행렬연산

전치행렬
- m x n행렬 A의 전치행렬(transpose matrix)은 A의 행을 열로, 열을 행으로 변경한 n x m행렬이다.
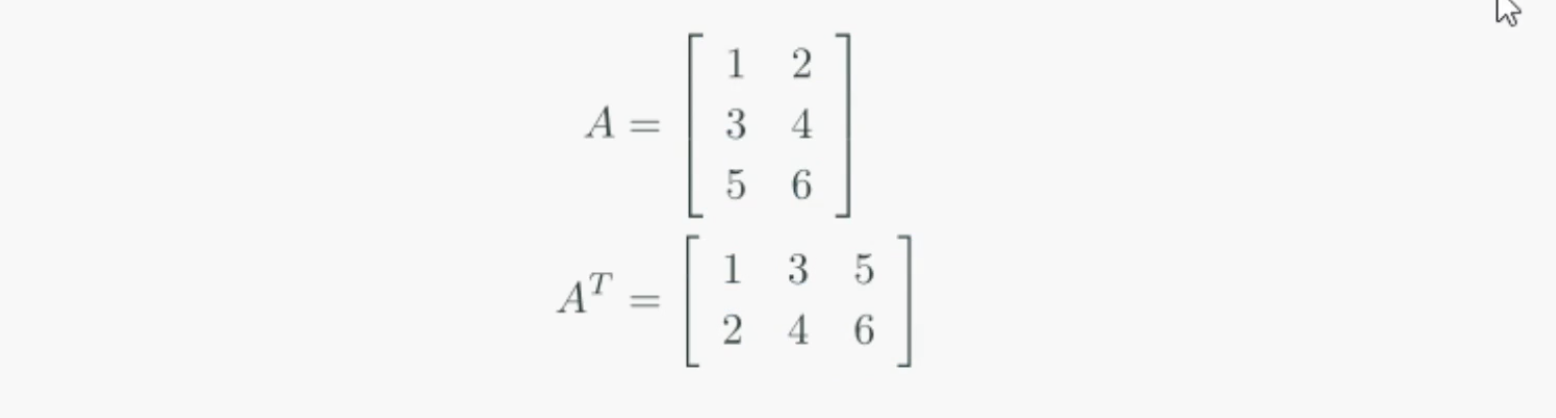
벡터

영행렬

- 항등원 : 어떤수를 연산했을 때 자기자신이 되는 수를 의미
정방행렬
- n x n과 같이 열과 행의 개수가 같은 정사각형 모양의 행렬
항등행렬
- 주대각선이 1이고 나머지는 0인 정방행렬을 항등행렬(identity matrix)라한다.
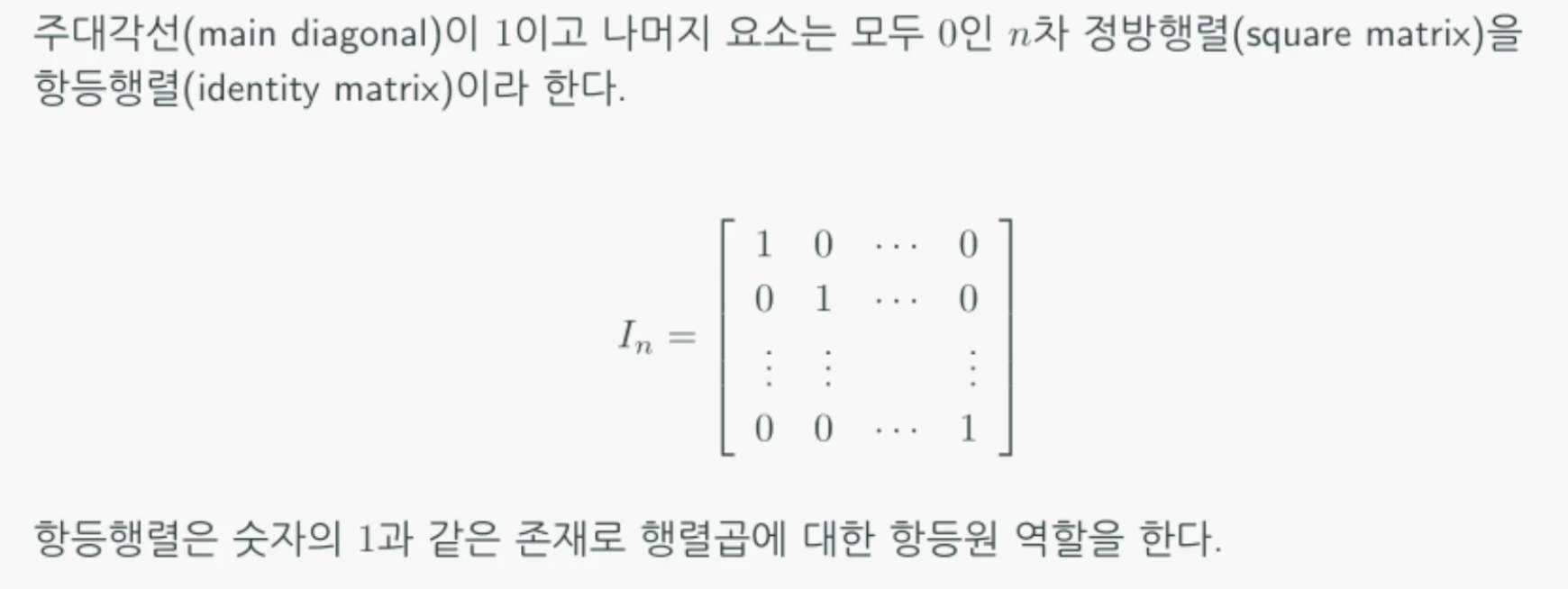
행렬의 곱
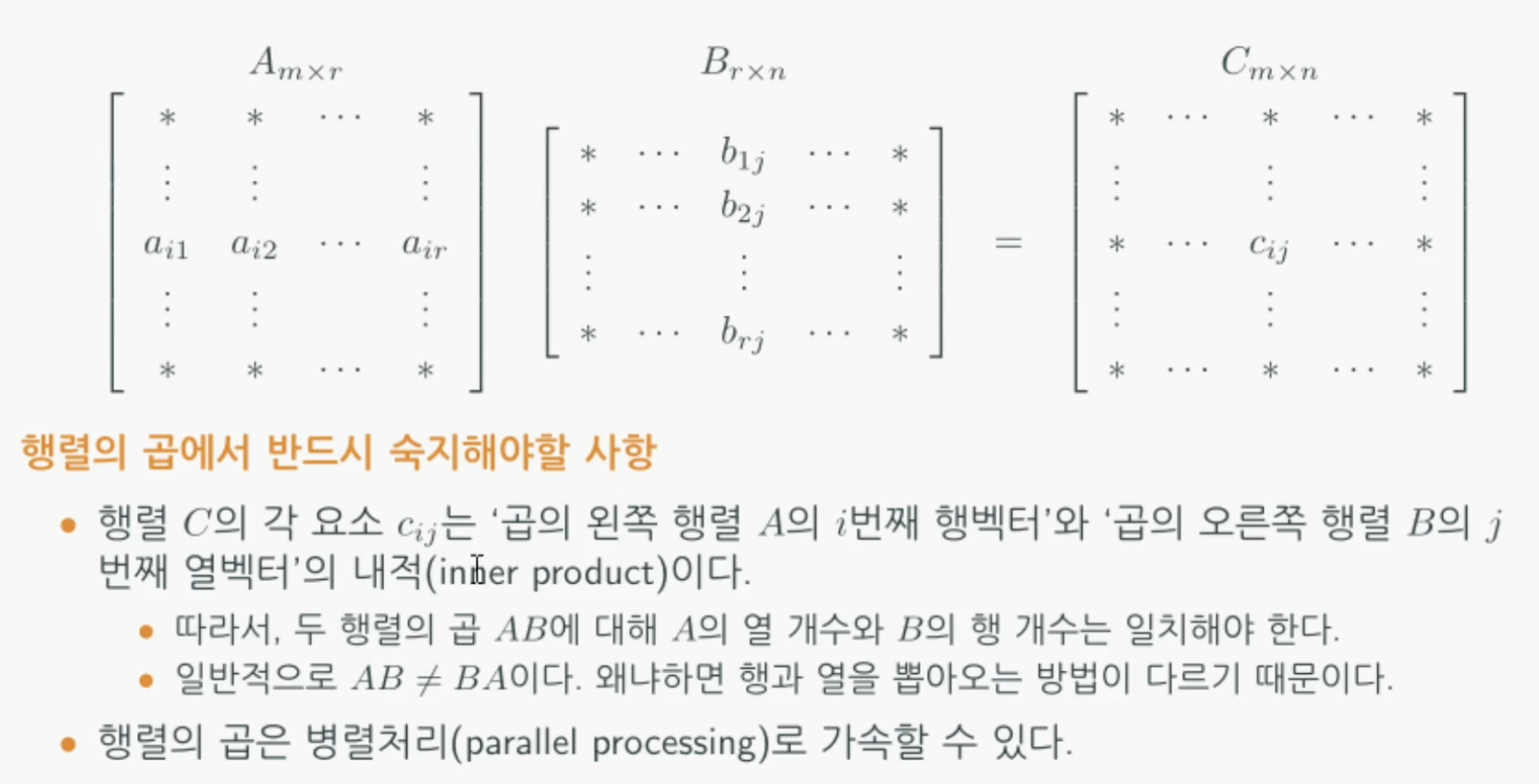
- 마지막에 병렬처리로 가속할 수 있다는 의미는 예를들어 c23의 요소는 A의 2번째 행과 B의 3번째 열의 내적이고 cij의 요소는 A의 i번째 행과 B의 j번째 열의 내적이므로 요소들간의 관계가 독립적인 것을 의미한다.
텐서(Tensor)의 구조
- 텐서라는 용어는 새로운 개념인데 간단하게만 알아보겠다.

- 위 그림의 T행렬의 요소를 각각의 픽셀(픽셀은 2-tensor)이라고하고 픽셀별 RGB색상 또는 RGBA가 있으면 방향이 하나 추가되므로 3-tensor가 된다.
- 4-tensor의 예는 RGB 색상이 시간에따라 변하는 즉 동영상의 경우를 생각해볼 수 있지만 시각적으로 표현해내기는 쉽지가 않다.
분할행렬(Partitioned Matrix)
분할행렬이란?
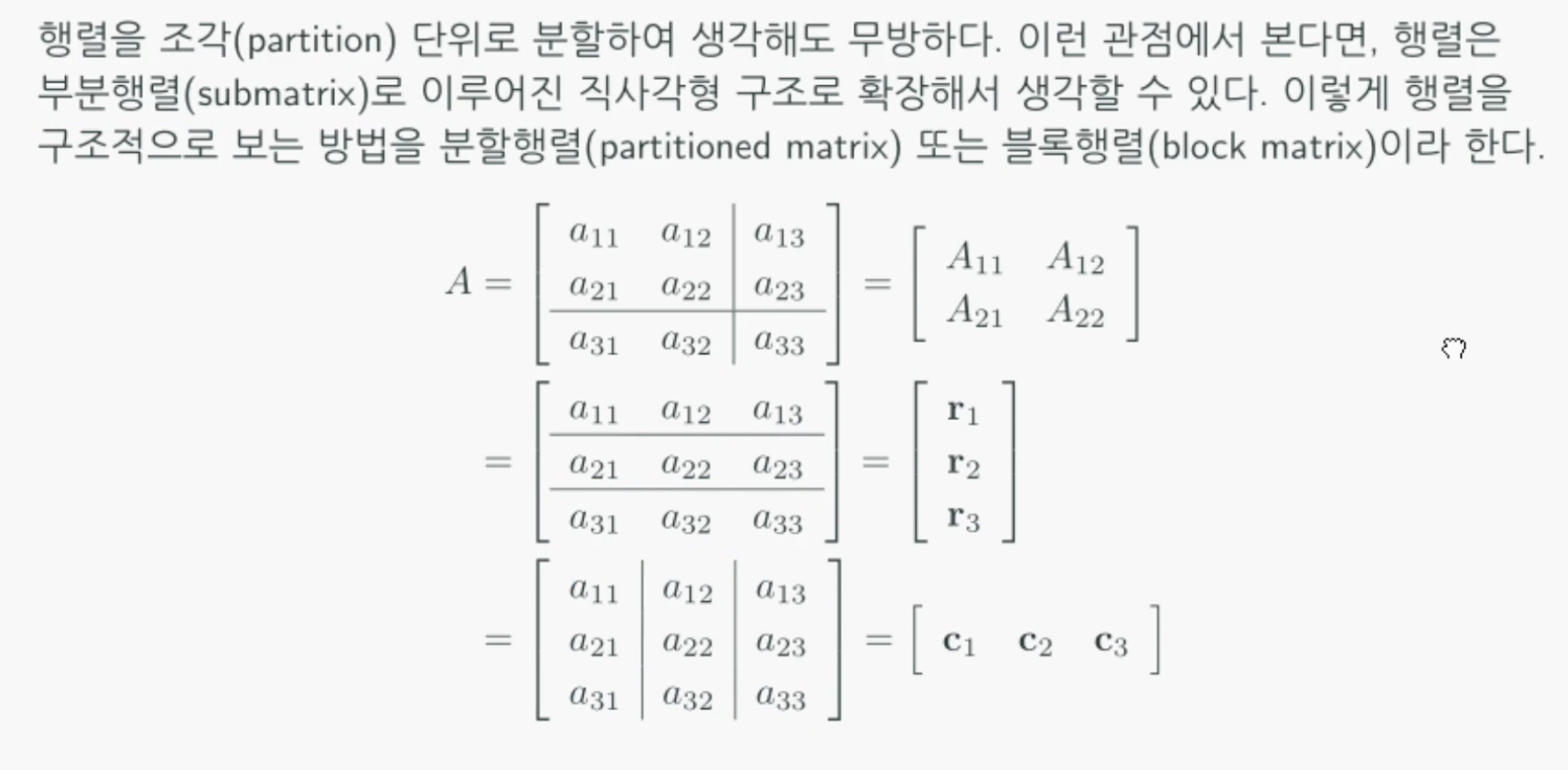
분할행렬의 곱
- 행렬의 곱 AB = C에서 B의를 분할된 열벡터의 모음으로 생각하면 다름과 같다.
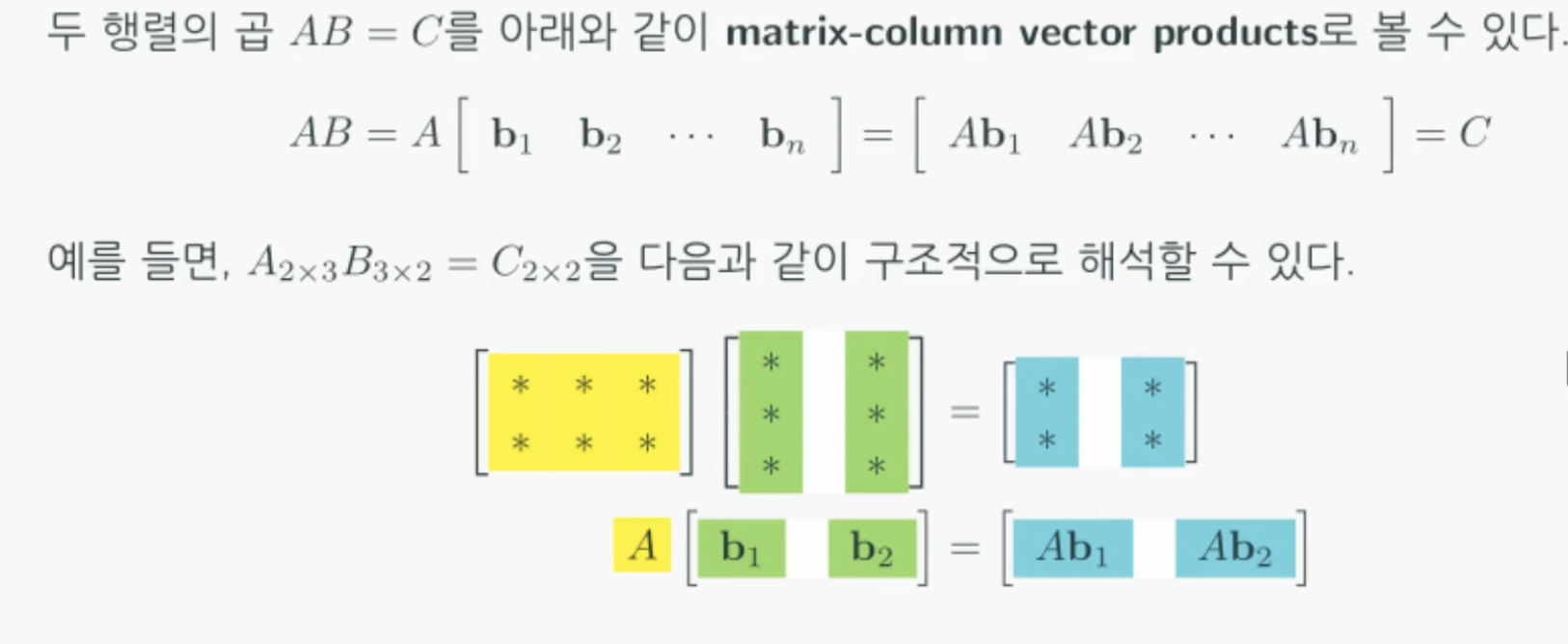
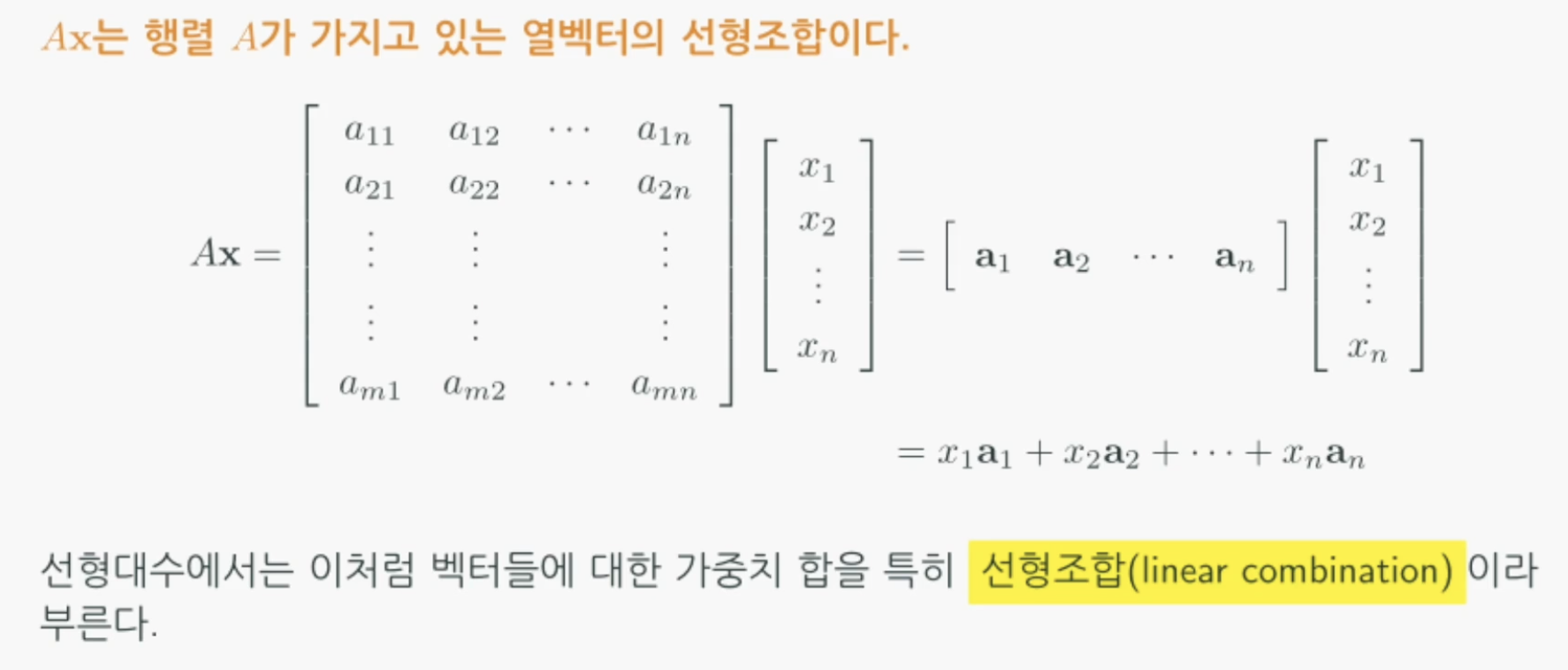
선형조합(Linear Combination)
- Ax = b의 선형시스템에서 A의 열벡터의 원소를 각각 가중치라고 했을때 가중치의 조합을 통해 b가 표현가능하다면 해는 있는 것이고 표현 불가능하면 해는 없다고 볼 수 있다.
- 다음은 A의 열벡터 원소의 조합으로 벡터 b를 만들 수 없기 때문에 해가 존재하지않는다.
- A의 열벡터들을 기하학적으로 보면 각각의 열벡의 조합으로 어떤 공간을 만들 수 있는데 이를 열공간(column space)라고한다. 만약 해가 존재한다면 우항 b가 그 열공간에 존재할 수 있는 것이고 해가 없다면 열공간에 존재할 수 없다는 의미를가진다.

좌표계 변환
- 행렬과 벡터의 곱을 아래와같이 좌표계(행렬)과 좌표값(벡터)로 볼수 있는 새로운 관점이다.
- 예를들어 아래 그림에서 [a,b] 벡터의 앞에서는 항등행렬 I가 곱해졌다고 볼수 있고 이를 오른쪽 식의 선형조합으로 나타낼 수 있다. 이때 벡터 v는 표준좌표계(항등행렬)에서 x축으로 a만큼 y축으로 b만큼 이동한 값이라고 볼 수있다.

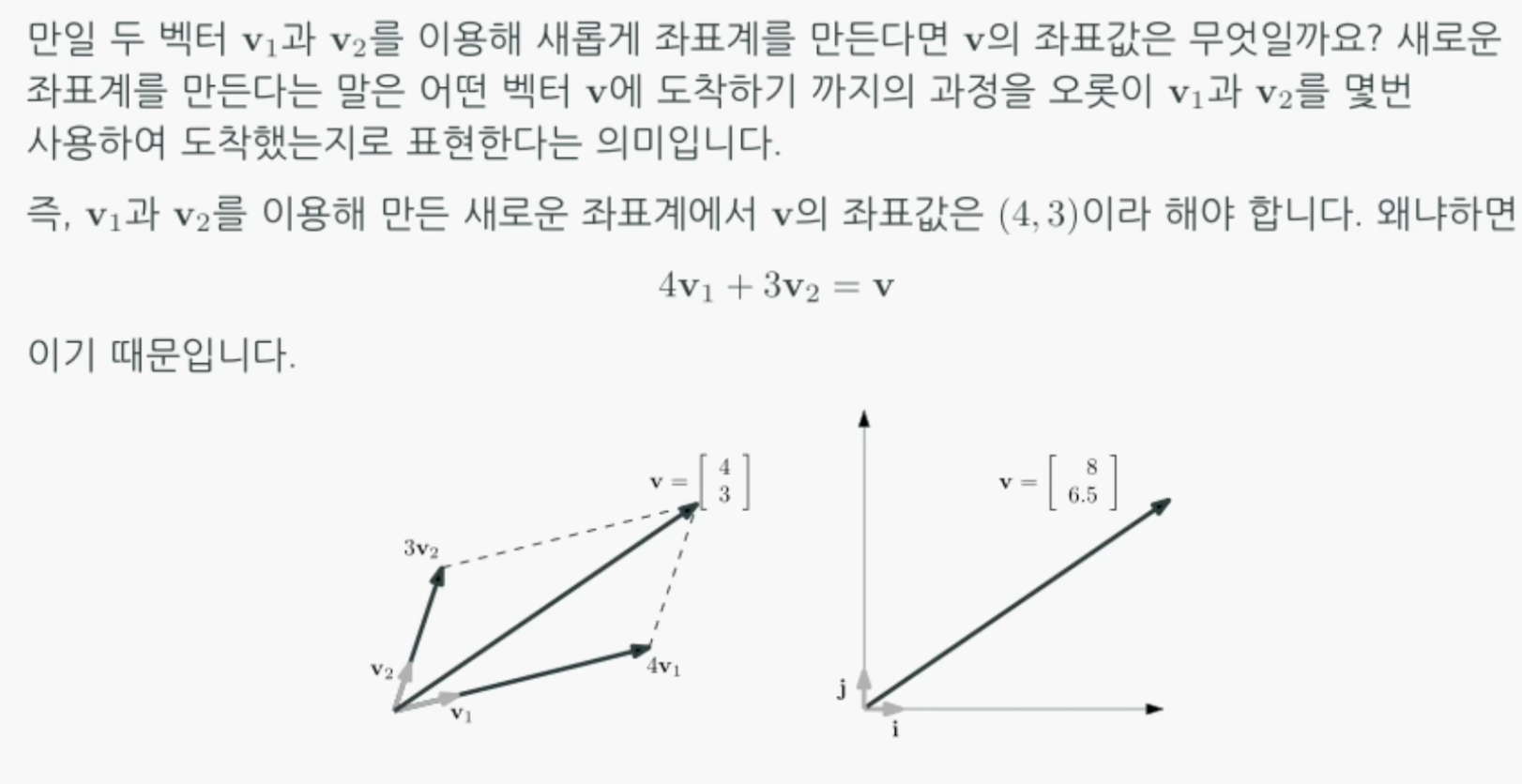
다음 그림을 보면 오른쪽은 표준좌표계(항등행렬)에 좌표값 [8,6.5]를 표현한 것이다. 이를 왼쪽그림처럼 v1, v2를 이용한 새로운 좌표계에 표현하면 좌표값은 [4,3]가 된다.
선형변환
- 먼저 초,중,고등 교육에서 배운 함수의 정의를 다시 리마인드 해보자.
함수를 쉽게 설명하면 어떤 input을 상자안에 넣었을 때 결과값 output이 나온다면 이때 그 박스를 함수라고 할 수 있다.
또한 함수는 두 집한 간의 mapping rule이다.
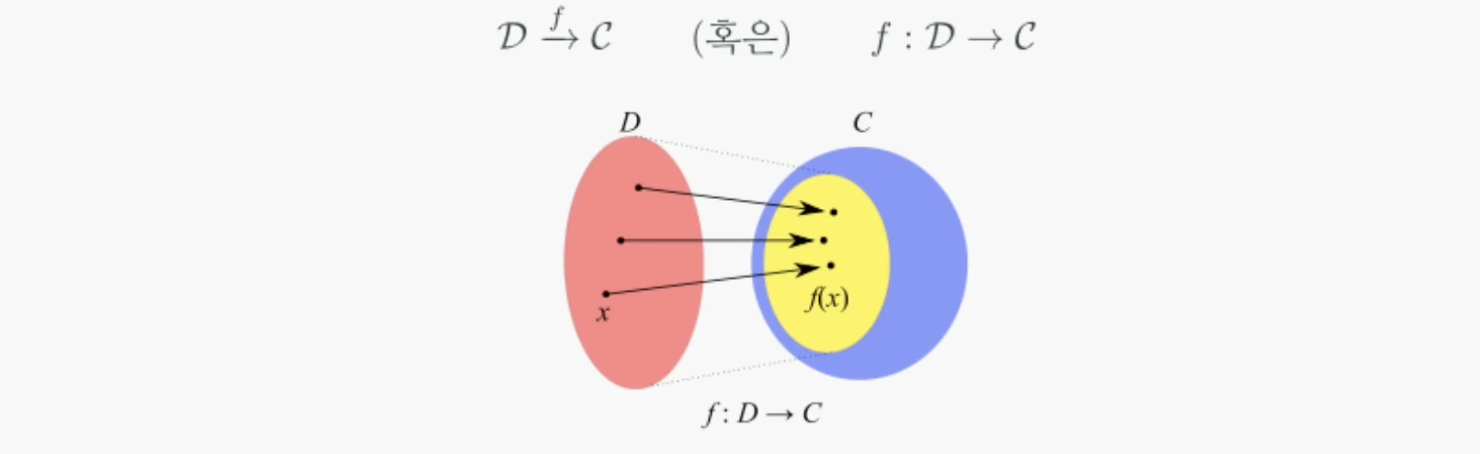
아래 그림에서 입력이 정의되는 D부분을 정의역(Domain)이라고 하고 출력이 정의되는 C부분을 공역(Codomain)이라고하며 공역 중 실제로 입력이 맵핑되어 나오는 부분(노란색)을 치역(range)라고한다.
선형함수(Linear function)
아래의 두 조건을 만족하는 함수 f를 선형함수라고 한다.
만약 선형을 만족하지 않는 예를 찾으려면 지수함수나 로그함수를 아래 x,y에 대입해보면 만족하지 않는 것을 알 수 있다.
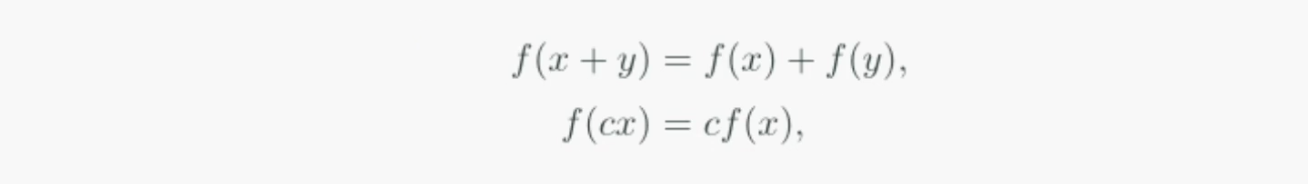
변환(Transformation)
- 함수 중에 입력(n-벡터)과 출력(m-벡터)이 벡터인 함수를 말한다. 그리고 만약 n = m(차수가 같을 때)인 경우 해당 변환을 연산자(operator)라고한다
- 행렬변환에서도 다음과 같이 만족한다. 이 때 A가 m x n행렬이라면 입력이 n차원이고 출력이 m차원임을 주의해야한다. 또한 행렬을 선형함수의 성질을 만족하기 때문에 선형변환이며 반대로 선형변환은 행렬로 표현이 가능하다.

표준행렬(Standard matrix)
- 행렬변환을 코딩하기위해서는 표준행렬을 구성하는 것이 필요하다.
표준행렬 구하는법n-차원 표준기저벡터 {e1, e2, e3, e4 ... en}을 생각한다.
위 표준기저벡터의 각 원소 ei에대해 우리가 원하는 기능(함수)을 동작시켜 얻은 결과인 m-차원 벡터를 표준행렬의 각 열에 적는다.
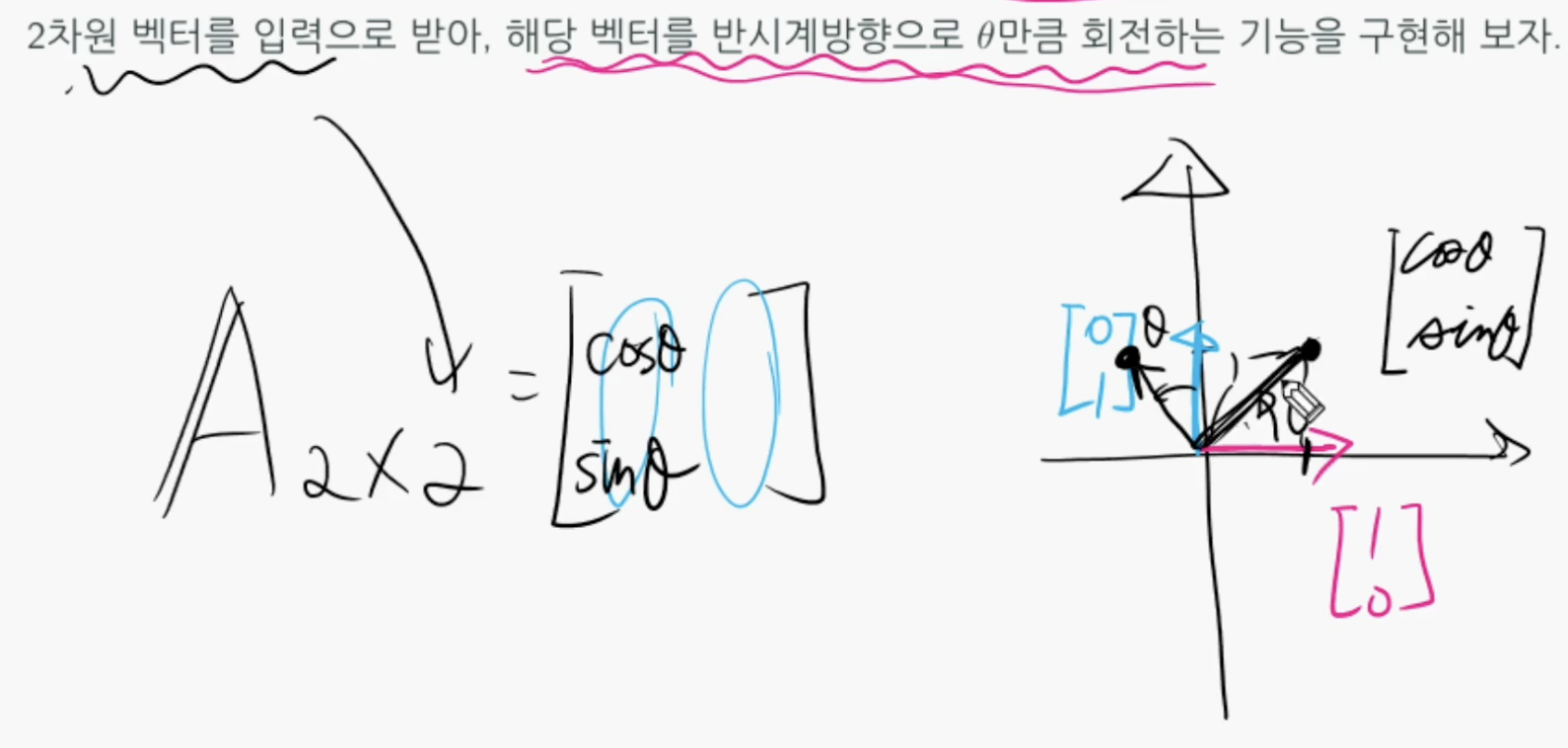
선형변환 코딩하기
- 구현하고자하는 기능(function)이 변환(입력과 출력이 벡터)인지 확인한다.
- 기능이 선형인지 확인한다.
- 입력이 n-벡터이고 출력이 m-벡터이면 m x n 표준행렬을 구성한다.
예시