그래프 탐색 알고리즘의 대표격이라 할 수 있는 DFS(깊이 우선 탐색)과 BFS(너비 우선 탐색)에 대해 알아보자.
깊이 우선 탐색 (DFS)
Depth First Search, 깊이 우선 탐색이란, 말 그대로 너비와 깊이 중 깊이를 우선하여 그래프를 탐색하는 방법이다. 어떤 노드와 연결된 다른 노드로 이동하고, 이동한 그 노드에 연결된 또 다른 노드로 이동한다.
DFS는 다음의 규칙으로 진행된다.
1. 노드와 연결된, 탐색하지 않은 이웃 노드 중 하나를 탐색한다.
2. 탐색하지 않은 이웃 노드가 없는 경우, 이전 노드로 돌아간다.
즉 탐색할 노드가 있는 한 어디까지고 깊게 파고 들어간다.
백문이 불어일견이라고 탐색하는 과정을 실제로 보자
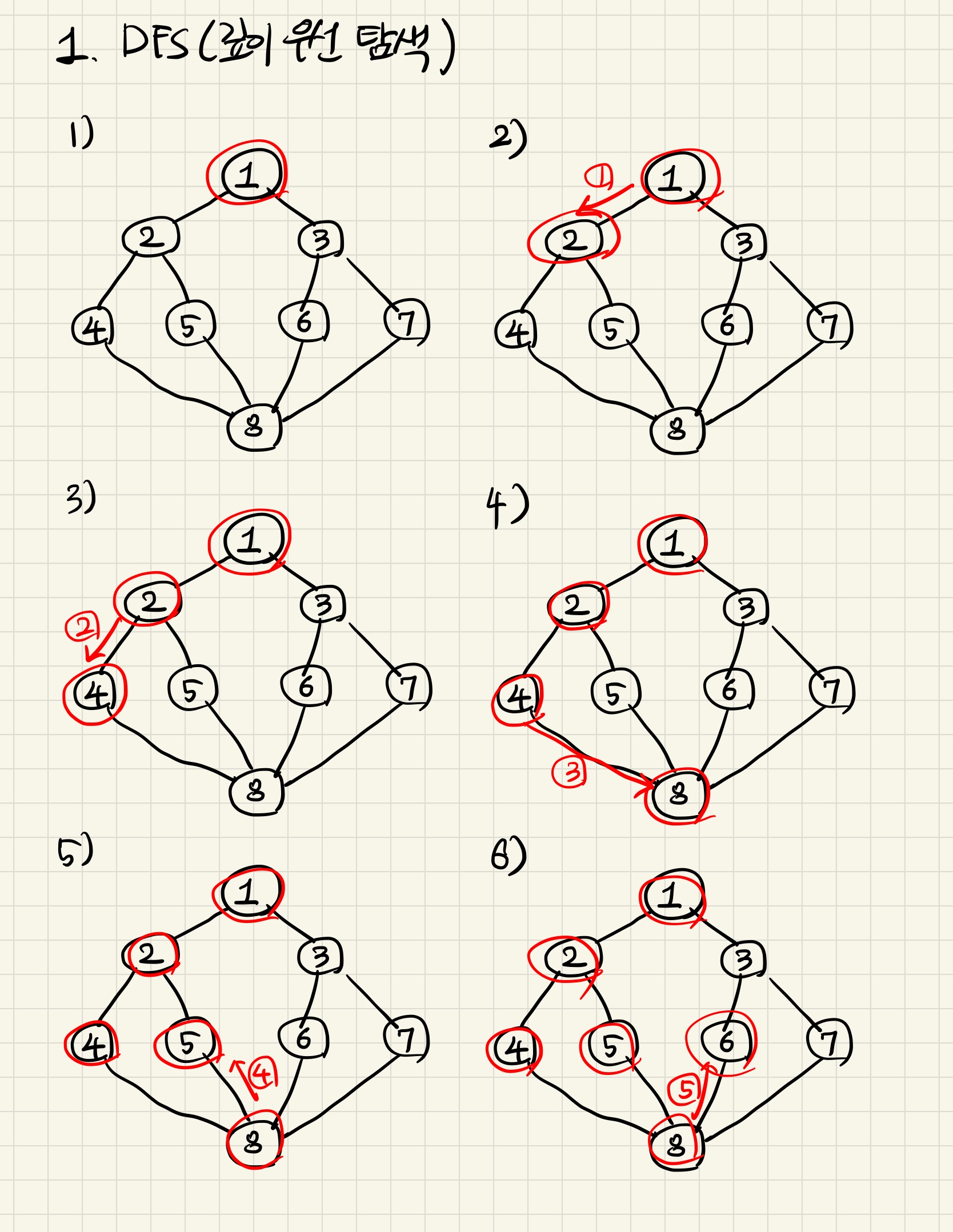
- 시작 노드는 임의로 1번으로 잡았다. 연결되어 있고, 아직 탐색하지 않은 노드 2, 3 중 2를 선택해 탐색한다.
- 다시, 2에 연결되어 있으며 탐색하지 않은 노드 4, 5 중 4를 탐색한다.
- 4는 8과 연결되어 있고 아직 탐색하지 않았으므로 8을 탐색한다.
- 8은 4, 5, 6, 7과 연결되어 있고 아직 탐색하지 않은 노드는 5, 6, 7이다. 이 중 5를 탐색한다.
- 5는 2, 8과 연결되어 있지만 공교롭게도 둘 다 이미 탐색이 되었다. 즉 이전 노드인 8로 돌아간다.
- 다시 8로 돌아왔다. 직전에 선택지 3개 5, 6, 7 중 5를 보았고, 6, 7이 남았는데 이 중 6을 탐색한다.
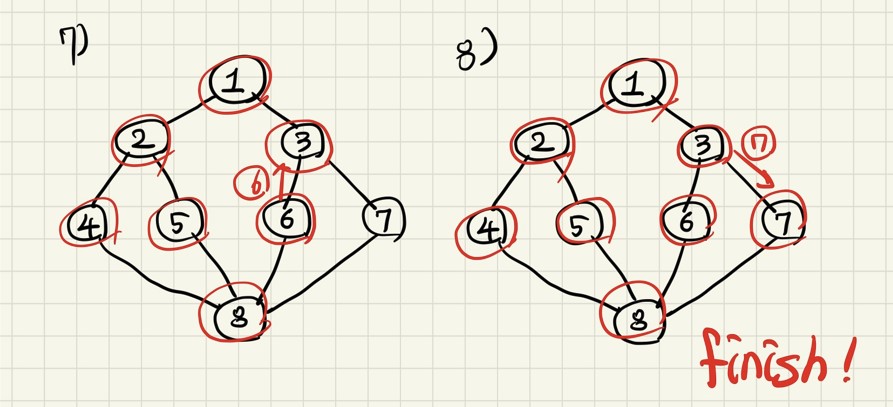
- 6에서 3으로 이동한다. 아직 탐색되지 않은 노드!
- 마지막, 3에서 7로 이동한다.
이리 하여 깊이 우선 탐색이 완료되었다.
DFS의 구현
DFS는 스택이나 재귀함수를 통해 구현이 가능하다.
스택은 후입선출(LIFO) 자료구조이기 때문에 가장 최근에 넣은 것들을 꺼내기 적합하며, 따라서 깊게깊게 파고 들어가야 하는 DFS에서 사용될 수 있다.
이동한 노드에서 다시 연결된 노드를 탐색하는 과정을 반복하기 때문에 재귀함수로도 구현이 가능할 것이다.
여러 개의 선택지가 있을 때 어떤 노드를 선택하느냐는 구현하기 나름이지만 일관성이 있는 것이 좋을 것이다. 이 글에서는 노드들 중 가장 번호가 작은 노드를 고르기로 하자. (위의 그림과 같다.)
스택을 이용한 DFS 구현
- 각 노드에서, 인접하고 방문하지 않은 노드들을 모두 스택에 넣는다.
- 스택에서 pop (해당 번호의 노드로 이동 했다는 뜻) 함과 동시에 방문 표시를 해 주고, 다시금 그 노드와 인접하고 방문하지 않은 노드들을 스택에 넣는다.
이 때, 여러 선택지 중 작은 번호의 노드부터 탐색하기로 하였으므로, 스택에 넣을 때는 큰 수부터 탐색하여 넣는다. 위의 그림에서 1과 인접한 노드가 2, 3인데, 그 다음으로 2를 탐색하려면 3, 2 순서로 넣어야 pop 했을 때 2가 올라올 테니까.
f = open("input.txt", "r")
g = int(f.readline())
graph = [[0 for _ in range(g)] for _ in range(g)]
stack = []
visited = [False for _ in range(g)]
answer = []
while True :
v = list(map(int, f.readline().split()))
if not v :
break
graph[v[0]][v[1]] = 1
graph[v[1]][v[0]] = 1
def dfs(n) :
stack.append(n)
while len(answer) != g :
v = stack.pop()
visited[v] = True
answer.append(v + 1)
for i in range(g-1, -1, -1) :
if graph[v][i] and not visited[i] :
stack.append(i)
print(*answer)
dfs(0)- 먼저 g개의 노드들이 있고, g by g의 2차원 리스트 graph를 만든다.
- graph 리스트에서, 서로 연결된 노드들은 1로 표시해준다.
- index 0 (위 그림에서는 1번) 을 인자로 넘겨주면서 시작하고, 먼저 1을 스택에 넣는다.
- 그 다음부터는 스택에서 pop 하면서 탐색을 시작한다. (index는 0~g-1이지만 편의상 1~g번으로 부르겠다.)
- 먼저 1번 노드로 이동한다. visited 리스트를 갱신 해주고, 탐색 순서를 출력할 answer 리스트에 append 한다.
- 그 후 1번과 인접한 노드들 중 방문하지 않은(not visited) 노드들을 stack에 push 해준다. 이 때 큰 숫자부터 집어넣는다.
- 위의 과정을 answer 리스트의 개수가 g개, 즉 모든 노드를 탐색할 때까지 반복한다.
재귀함수를 이용한 DFS 구현
# 윗부분 동일
def dfs(n) :
print(n + 1, end =" ")
visited[n] = True
for i in range(g) :
if graph[n][i] and not visited[i] :
dfs(i)
dfs(0)
코드가 많이 간결해졌다. 해당 노드를 출력하고, 방문했다는 표시로 visited를 갱신해준다. 그 후에 인접하고 방문하지 않은 노드를 발견하면, 그 노드 번호를 가지고 다시 dfs를 호출한다. 그렇다면 n 자리에 그 번호가 들어가게 될 것이고 출력되고, visited도 갱신될 것이고 착착착 진행될 것이다.
만약 이동할 수 있는 노드가 없다면 for loop 안에 if문에 걸리지 않게 되어 아무 일 없이 함수가 종료되고, 이전 노드로 돌아가는 효과를 낳는다.
예를 들어 맨 처음에 dfs(1)을 호출했을 때 for문을 돌면서 dfs(2), dfs(3)을 차례로 호출할 것인데, 2를 시작으로 쭉쭉 파고들었을 때 더이상 탐색할 노드가 없을 때 비로소 dfs(1)에서 호출한 dfs(2)가 종료되고 dfs(3)이 시작된다.
끝
다음에는 DFS의 자매품인 너비 우선 탐색(BFS)에 대해.araboza
