문제
두 문자열 A와 B가 주어졌을 때, A에 연산을 최소 횟수로 수행해 B로 만드는 문제를 "최소 편집" 문제라고 한다.
A에 적용할 수 있는 연산은 총 3가지가 있으며 아래와 같다.
- 삽입: A의 한 위치에 문자 하나를 삽입한다.
- 삭제: A의 문자 하나를 삭제한다.
- 교체: A의 문자 하나를 다른 문자로 교체한다.
두 문자열이 주어졌을 때, 최소 편집 횟수를 구하는 프로그램을 작성하시오.
입력
첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 소문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.
출력
첫째 줄에 최소 편집 횟수를 출력한다.
이론 설명
편집 거리(Edit Distance) 알고리즘, 혹은 리벤슈타인 거리(Levenshtein Distance) 문제라고도 한다.
문자열 A와 문자열 B가 있을 때, A의 문자를 삭제, 변경 혹은 삽입하여 B의 문자열을 만들어야 할 때, 최소 횟수를 구하는 문제이다.
예를 들어 'sunday' 와 'saturday' 가 있을 때, 's' 뒤에 'a'를 삽입하고(saunday), 'a' 뒤에 't'를 삽입하고(satunday), 'n'을 'r'로 변경하면(saturday) 'saturday' 를 얻을 수 있다.
자칫 난해해 보일 수도 있겠으나 하나하나 뜯어보면서 식을 세우고 점화식을 세움으로써 dp로 풀 수 있다.
예를 들어보자.
abcd 라는 문자열을 bcde로 수정하고자 한다.
결과적으로 bcde 라는 문자열을 얻으려면 어떻게 해야 할까?
- 길이가 하나 짧은 문자열에서 하나를 추가하거나 (가령
bcd->bcde) - 길이가 하나 긴 문자열에서 하나를 제거하거나 (가령
bcdef->bcde) - 길이가 같은 문자열에서 하나를 변경하거나 (가령
bcda->bcde)
세 가지 경우의 수 중 한가지 일 것이다.
그렇다면 저 세 가지 방법 중 가장 작은 횟수의 방법에서 +1 하면 얻을 수 있을 것이다.
예시
문자열 EXPONENTIAL을 POLYNOMIAL 로 수정하고 싶다.
EXPONENTIAL 의 길이를 m, POLYNOMIAL 의 길이를 n이라고 하였을 때 (m+1) by (n+1) 의 2차원 리스트를 만들어 보자. 그럼 12 by 11의 리스트일 것이고 0으로 초기화 해주자.
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
1행부터 12행까지 0, E, X, P, O ... I, A, L을 붙여 주고, 1열부터 11열까지 0, P, O, L, Y ... I, A, L을 붙여 준다.
그리고 이 리스트의 [i][j] 번째 리스트가 의미하는 것은
0~i번째까지의 문자열에서, 0~j번째까지의 문자열로 수정하는 데 드는 최소 횟수
이다. (0번째라고 함은, 아무것도 없는 상태(null)을 의미한다.)
예를 들어 [1][1] 이라고 함은, E에서 P로 수정하는 데 드는 최소 횟수이고,
[4][5] 이라고 함은 EXPO에서 POLYN로 수정하는 데 드는 최소 횟수이다.
그럼 [0][j]는? 무(NULL)에서 j개를 내리 붙여야 하므로 당연히 j번일 것이고
[i][0]은? i개에서 무(NULL)로 만들어야 하기 때문에 i개를 내리 삭제해야 하므로 i번일 것이다.
즉, 각 1행과 1열은 0에서부터 1씩 증가하면서 채워진다.
0 1 2 3 4 5 6 7 8 9 10
1 0 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0 0
5 0 0 0 0 0 0 0 0 0 0
6 0 0 0 0 0 0 0 0 0 0
7 0 0 0 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0 0 0
9 0 0 0 0 0 0 0 0 0 0
10 0 0 0 0 0 0 0 0 0 0
11 0 0 0 0 0 0 0 0 0 0
세로 '에서' 가로 '로' 만든다.로 생각하자.
이제 [1][1]부터 [m][n]은 이전 항과의 점화식 관계를 세워서 채워 넣을 수 있다.
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
하지만 여기서 고려해 주어야 할 것은, 문자열 A의 i번째 문자와 문자열 B의 j번째 문자가 같아서 별다른 수정을 하지 않아도 될 때이다. 이 경우에는 +1을 할 필요 없이 이어 붙여 나갈 수 있다.
즉 word1[i]와 word2[j]가 같은지 여부를 먼저 살펴볼 필요가 있다.
따라서 조건식을 완성해보면 다음과 같다.
if word1[i] == word[j] :
dp[i][j] = dp[i-1][j-1]
else :
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1위 조건식대로 리스트를 마저 채워나가면 다음과 같이 채워진다.
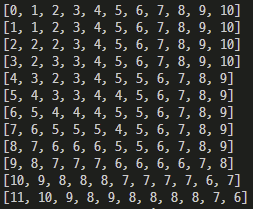
그리고 우리가 찾는, EXPONENTIAL에서 POLYNOMIAL로 수정하는 방법의 최소 횟수는 리스트의 가장 우측 하단, 즉 dp[len(word1)][len(word2)] 인 6 일 것이다.
딱 이 알고리즘을 이용할 수 있는 백준 문제는 15483번, 최소 편집 문제이다.
전체 코드는 다음과 같다.
word1 = input()
word2 = input()
len1 = len(word1)
len2 = len(word2)
dp = [[0] * (len2 + 1) for _ in range(len1 + 1)]
for i in range(1, len1 + 1) :
dp[i][0] = i
for i in range(1, len2 + 1) :
dp[0][i] = i
for i in range(1, len1 + 1) :
for j in range(1, len2 + 1) :
if word1[i-1] == word2[j-1] :
dp[i][j] = dp[i-1][j-1]
else :
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
print(dp[len1][len2])결과

